无约束最优化方法
无约束优化方法
求解无约束最优化的基本思路
- 给定初始点 x 0 ∈ R n , k = 0 x_0\in \mathbb{R}^n,k=0 x0∈Rn,k=0
- 判断当前解是否满足终止准则,若满足则停止迭代,若不满足则转3.
- 确定 f ( x ) f(x) f(x)在 x k x_k xk点的下降方向
- 确定步长 λ k \lambda_k λk,使 f ( x k + λ k d k ) f(x_k+\lambda_k d_k) f(xk+λkdk)较之 f ( x k ) f(x_k) f(xk)有某种意义的下降
- 令 x k + 1 = x k + λ k d k , k = k + 1 x_{k+1}=x_k+\lambda_k d_k,k=k+1 xk+1=xk+λkdk,k=k+1 ,转2.
终止准则
- 对于无约束优化问题,适用于收敛速度较慢的算法准则为 ∥ ∇ f ( x k ) ∥ ⩽ ε \Vert{\nabla f(x_k)}\Vert\leqslant \varepsilon ∥∇f(xk)∥⩽ε
- 当算法具有超线性收敛性时,较为合适的准则为 ∥ x k + 1 − x k ∥ ⩽ ε \Vert{x_{k+1}-x_k}\Vert\leqslant \varepsilon ∥xk+1−xk∥⩽ε
- 对于快速收敛的算法,相当有效的准则为 ∣ f ( x k + 1 ) − f ( x k ) ∣ ⩽ ε \vert{f(x_{k+1})-f(x_k)}\vert\leqslant \varepsilon ∣f(xk+1)−f(xk)∣⩽ε
非凸优化变为凸优化
- 修改目标函数,用凸函数近似目标函数
- 放松约束条件,将可行域替换为其凸包(集合内所有点的凸组合)
- 求解拉格朗日对偶问题,无论原问题是否为凸优化问题,其拉格朗日对偶问题一定是凸优化问题
有约束问题转化为无约束问题
- 具有强对偶性质的优化问题可以求解其拉格朗日对偶问题,进而得到原问题的最优解
- 罚函数法:根据约束条件构造惩罚函数,之后按照无约束优化问题求解
最速下降法,牛顿法,拟牛顿法统一公式描述
{ x k + 1 = x k + λ d k d k = − D k ∇ f ( x k ) \begin{cases}x_{k+1}=x_{k}+\lambda d_{k}\\ d_{k}=-D_{k}\nabla f\left( x_{k}\right) \end{cases} {xk+1=xk+λdkdk=−Dk∇f(xk)
对于最速下降法 D k = I D_k=I Dk=I
对于牛顿法 D k = [ ∇ 2 f ( x k ) ] − 1 D_{k}=\left[ \nabla ^{2}f\left( x_{k}\right) \right] ^{-1} Dk=[∇2f(xk)]−1
对于拟牛顿法 D k D_k Dk为Hesse矩阵的逆矩阵的逼近矩阵
一维线搜索
精确一维线搜索
- 二分法
- Dichotomous法
- Fibonacci法
- 黄金分割法
- Shubert_Piyavskii法
不精确一维线搜索
Goldstein准则
( 1 ) f ( x ( k + 1 ) ) − f ( x ( k ) ) ≤ ρ λ k ∇ f T ( x ( k ) ) d ( k ) ( 2 ) f ( x ( k + 1 ) ) − f ( x ( k ) ) ≥ ρ λ k ∇ f T ( x ( k ) ) d ( k ) (1) f(x^{(k+1)})-f(x^{(k)})\leq \rho \lambda_k \nabla f^T(x^{(k)})d^{(k)}\\ (2) f(x^{(k+1)})-f(x^{(k)})\geq \rho \lambda_k \nabla f^T(x^{(k)})d^{(k)} (1)f(x(k+1))−f(x(k))≤ρλk∇fT(x(k))d(k)(2)f(x(k+1))−f(x(k))≥ρλk∇fT(x(k))d(k)
Wolfe准则
I n e x a c t − s e a r c h − a l g o r i t h m 1. c h o o s e i n i t i a l p o i n t x 0 , i n i t i a l s e c t i o n [ 0 , λ max ] , ρ ∈ ( 0 , 1 2 ) , σ ∈ ( ρ , 1 ) L e t λ L = 0 , λ U = λ m a x , c a l c u l a t e ϕ L = f ( x k ) , ϕ L ′ = g T ( x k ) d k , λ M ∈ ( λ L , λ U ) 2. ϕ ( λ ) = f ( x k + λ d k ) I f ϕ ( λ M ) − ϕ ( λ L ) ≤ ρ α ϕ ′ ( λ L ) , t u r n t o 3. O t h e r w i s e a c c o r d n g t o q u a d r a t i c i n t e r p o l a t i o n ( 2 p o i n t s , 1 d e r i v a t i v e ) A s s u m i n g ϕ ( λ ) = a λ 2 + b λ + c ϕ ′ ( λ ) = 2 a λ + b { ϕ ( λ L ) = a λ L 2 + b λ L + c ϕ ( λ M ) = a λ M 2 + b λ M + c ϕ ′ ( λ L ) = 2 a λ L + b ⇒ { ϕ ( λ M ) − ϕ ( λ L ) = a ( λ M 2 − λ L 2 ) + b ( λ M − λ L ) ( λ M − λ L ) ϕ ′ ( λ L ) = 2 a λ L ( λ M − λ L ) + b ( λ M − λ L ) ⇒ ( λ M − λ L ) ϕ ′ ( λ L ) − ϕ ( λ M ) + ϕ ( λ L ) = − a ( λ M − λ L ) 2 ⇒ { a = − ( λ M − λ L ) ϕ ′ ( λ L ) − ϕ ( λ M ) + ϕ ( λ L ) ( λ M − λ L ) 2 b = ϕ ′ ( λ L ) − 2 λ L a − b 2 a = λ L + 1 2 ⋅ ϕ ′ ( λ L ) ( λ M − λ L ) 2 ( λ M − λ L ) ϕ ′ ( λ L ) − ϕ ( λ M ) + ϕ ( λ L ) L e t λ U = λ M , λ M = λ ‾ , t u r n t o 2. 3. C a l c u l a t e ϕ ′ ( λ M ) = g ( x k + λ M d k ) T d k , I f ϕ ′ ( λ M ) ⩾ σ ϕ ′ ( λ L ) , l e t λ k = λ M , r e t u r n ; O t h e r w i s e a c c o r d i n g t o q u a d r a t i c i n t a p d a t i o n ( 1 p o i n t , 2 d e r i v a t i v e s ) { ϕ ( λ L ) = a λ L 2 + b λ L + c ϕ ′ ( λ L ) = 2 a λ L + b ϕ ′ ( λ M ) = 2 a λ M + b ⇒ { a = ϕ ′ ( λ M ) − ϕ ′ ( λ L ) 2 ( λ M − λ L ) b = ϕ ′ ( λ M ) − 2 a λ M λ ‾ = − b 2 a = λ M − ϕ ′ ( λ M ) ( λ M − λ L ) ϕ ′ ( λ M ) − ϕ ′ ( λ L ) L e t λ L = λ M , λ M = λ ‾ , t u r n t o 2. \begin{array}{l}Inexact-search-algorithm\\ {\Large\bf{1.}} choose\ initial\ point\ x_{0}\ ,\ initial\ section\left[ 0,\lambda \max \right] ,\rho\in \left( 0,\dfrac{1}{2}\right) ,\sigma\in \left( \rho,1\right) \\ Let\ \lambda _{L}=0,\lambda_U=\lambda_max ,calculate\ \phi _{L}=f\left( x_{k}\right) ,\phi _{L}'=g^{T}\left( x_{k}\right) d_{k},\lambda _{M}\in \left( \lambda _{L},\lambda_U\right) \\ {\Large\bf{2.}} \phi \left( \lambda \right) =f\left( x_{k}+\lambda d_k\right)\ If\ \phi \left( \lambda _{M}\right) -\phi \left( \lambda_L \right) \leq \rho \alpha \phi '\left( \lambda_{L}\right) ,turn\ to\ 3.\\ Otherwise\ accordng\ to\ quadratic\ interpolation\left( 2\ points,1\ derivative\right) \\ Assuming\ \phi \left( \lambda \right) =a\lambda ^{2}+b\lambda +c\quad \phi '\left( \lambda \right) =2a\lambda +b\\ \begin{cases}\phi \left( \lambda _{L}\right) =a\lambda _{L}^{2}+b\lambda _{L}+c\\ \phi \left( \lambda_{M}\right) =a\lambda _{M}^{2}+b\lambda_M+c\\ \phi '\left( \lambda _{L}\right) =2a\lambda _{L}+b\end{cases}\\ \Rightarrow\begin{cases}\phi \left( \lambda_{M}\right) -\phi \left( \lambda _{L}\right) =a\left( \lambda_M ^{2}-\lambda _{L}^{2}\right) +b\left( \lambda_M-\lambda_L\right) \\ \left( \lambda_M-\lambda_{L}\right) \phi '\left( \lambda_{L}\right) =2a\lambda _{L}\left( \lambda_M-\lambda_L\right) +b\left( \lambda_M-\lambda_L\right) \end{cases}\\ \Rightarrow \left( \lambda_M-\lambda_{L}\right) \phi '\left( \lambda_{L}\right) -\phi \left( \lambda_{M}\right) +\phi \left( \lambda_{L}\right) =-a\left( \lambda_M-\lambda_{L}\right) ^{2}\\ \Rightarrow \begin{cases}a=-\dfrac{\left( \lambda_M-\lambda _{L}\right) \phi '\left( \lambda_{L}\right) -\phi \left( \lambda_M\right) +\phi \left( \lambda_L\right) }{\left( \lambda_M-\lambda_{L}\right) ^{2}}\\ b=\phi '\left( \lambda_{L}\right) -2\lambda_{L}a\end{cases}\\ -\dfrac{b}{2a}=\lambda_{L}+\dfrac{1}{2}\cdot \dfrac{\phi '\left( \lambda_{L}\right) \left( \lambda_M-\lambda _{L}\right) ^{2}}{\left( \lambda_M-\lambda_{L}\right) \phi '\left( \lambda_{L}\right) -\phi \left( \lambda_M\right) +\phi \left( \lambda_L\right) }\\ Let\ \lambda_U=\lambda_{M},\lambda_M=\overline{\lambda},turn\ to\ 2.\\ {\Large\bf{3.}}Calculate\ \phi '\left( \lambda_M\right) =g\left( x_{k}+\lambda_M d_{k}\right) ^{T}d_{k},If\ \phi '\left( \lambda_{M}\right) \geqslant \sigma\phi '\left( \lambda _{L}\right) ,let\lambda _{k}=\lambda_{M}, return; \\Otherwise\ according\ to\ quadratic\ intapdation \left( 1\ point,2\ derivatives\right) \\ \begin{cases}\phi \left( \lambda _{L}\right) =a\lambda _{L}^{2}+b\lambda_L+c\\ \phi '\left( \lambda_L\right) =2a\lambda_L+b\\ \phi '\left( \lambda_{M}\right) =2a\lambda_{M}+b \end{cases}\\ \Rightarrow\begin{cases} a=\dfrac{\phi '\left( \lambda_M\right) -\phi '\left( \lambda_L\right) }{2( \lambda_M-\lambda_L)}\\ b= \phi '\left( \lambda_M\right) -2a\lambda_M\end{cases}\\ \overline{\lambda }=-\dfrac{b}{2a}=\lambda_M-\dfrac{\phi '\left( \lambda_M\right) \left( \lambda_M-\lambda_L\right) }{\phi '\left( \lambda_{M}\right) -\phi '\left( \lambda_L\right) }\\ Let\ \lambda _{L}=\lambda_M,\lambda _M=\overline{\lambda},turn\ to\ 2.\end{array} Inexact−search−algorithm1.choose initial point x0 , initial section[0,λmax],ρ∈(0,21),σ∈(ρ,1)Let λL=0,λU=λmax,calculate ϕL=f(xk),ϕL′=gT(xk)dk,λM∈(λL,λU)2.ϕ(λ)=f(xk+λdk) If ϕ(λM)−ϕ(λL)≤ραϕ′(λL),turn to 3.Otherwise accordng to quadratic interpolation(2 points,1 derivative)Assuming ϕ(λ)=aλ2+bλ+cϕ′(λ)=2aλ+b⎩ ⎨ ⎧ϕ(λL)=aλL2+bλL+cϕ(λM)=aλM2+bλM+cϕ′(λL)=2aλL+b⇒{ϕ(λM)−ϕ(λL)=a(λM2−λL2)+b(λM−λL)(λM−λL)ϕ′(λL)=2aλL(λM−λL)+b(λM−λL)⇒(λM−λL)ϕ′(λL)−ϕ(λM)+ϕ(λL)=−a(λM−λL)2⇒⎩ ⎨ ⎧a=−(λM−λL)2(λM−λL)ϕ′(λL)−ϕ(λM)+ϕ(λL)b=ϕ′(λL)−2λLa−2ab=λL+21⋅(λM−λL)ϕ′(λL)−ϕ(λM)+ϕ(λL)ϕ′(λL)(λM−λL)2Let λU=λM,λM=λ,turn to 2.3.Calculate ϕ′(λM)=g(xk+λMdk)Tdk,If ϕ′(λM)⩾σϕ′(λL),letλk=λM,return;Otherwise according to quadratic intapdation(1 point,2 derivatives)⎩ ⎨ ⎧ϕ(λL)=aλL2+bλL+cϕ′(λL)=2aλL+bϕ′(λM)=2aλM+b⇒⎩ ⎨ ⎧a=2(λM−λL)ϕ′(λM)−ϕ′(λL)b=ϕ′(λM)−2aλMλ=−2ab=λM−ϕ′(λM)−ϕ′(λL)ϕ′(λM)(λM−λL)Let λL=λM,λM=λ,turn to 2.
多维搜索
不使用导数的方法
坐标轮换法
坐标轴作为搜索方向,沿方向 , , ⋯ , _, _, ⋯ , _ d1,d2,⋯,dn搜索,其中 _ dj是除第个位置为1,别的位置为0的向量,每次只改变第个变量,其它变量保持不动。
-
如果函数可微,梯度存在,最小化坐标方向时优先选择偏导数成份幅度最大的方向进行最小化
-
这种顺序一维最小化有时称为Gauss-Seidel迭代,可用于解线性方程组
-
该方法与最速下降法的收敛速度相当
函数可微时,方法会收敛到梯度为0的点,但不可微时,则可能 会在非最优点停止。
这种沿方向 x k + 1 − x k x_{k+1}-x_{k} xk+1−xk搜索的方式在坐标轮换方法中经常使 用,有时函数可微时也这样,并且固定次迭代后进行一次这样的搜索,通常会加速收敛,称为加速步。
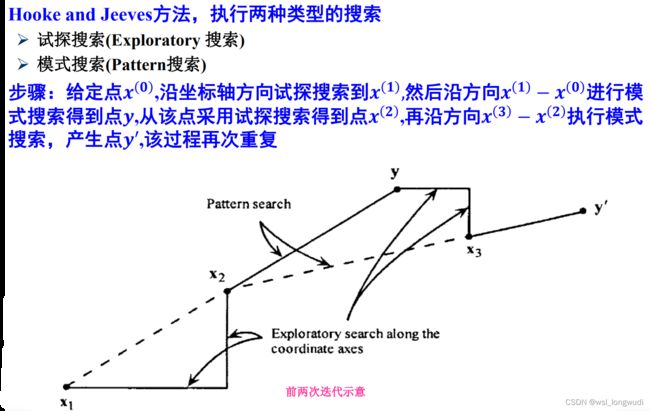
使用导数的方法
最速下降法(梯度下降)
Theory f : R n → R f:\mathbb{R}^n\to \mathbb{R} f:Rn→R在 x x x处可微,假设 ∇ f ( x ) ≠ 0 \nabla f(x)\neq 0 ∇f(x)=0,则下述问题的解即为 f ( x ) f(x) f(x)在 x x x处的最速下降方向
min d f ′ ( x ; d ) = lim λ → 0 + f ( x + λ d ) − f ( x ) λ = ∇ f ( x ) T d s . t . ∥ d ∥ = 1 ⇒ d ‾ = − ∇ f ( x ) ∥ ∇ f ( x ) ∥ \begin{aligned}\min _{d}f'\left( x;d\right) =\lim _{\lambda \rightarrow 0^{+}}\dfrac{f\left( x+\lambda d\right) -f\left( x\right) }{\lambda }=\nabla f\left( x\right) ^{T}d\quad s.t. \left\| d\right\| =1\\ \Rightarrow \overline{d}=-\dfrac{\nabla f\left( x\right) }{\left\| \nabla f\left( x\right) \right\| }\end{aligned} dminf′(x;d)=λ→0+limλf(x+λd)−f(x)=∇f(x)Tds.t.∥d∥=1⇒d=−∥∇f(x)∥∇f(x)
前后两次搜索方向正交
x k + 1 = x k + λ k d k λ k = arg min λ f ( x k + λ d k ) d f d λ = ∇ f T ( x k + λ d k ) d k = d k + 1 T d k = 0 \begin{array}{l}x_{k+1}=x_k+\lambda _{k}d_k\\ \lambda _{k}=\arg \min _{\lambda }f\left( x_k+\lambda d_k\right) \\ \dfrac{df}{d\lambda }=\nabla f^{T}\left( x_k +\lambda d_k\right) d_k=d^{T}_{k+1}d_k=0\end{array} xk+1=xk+λkdkλk=argminλf(xk+λdk)dλdf=∇fT(xk+λdk)dk=dk+1Tdk=0
牛顿法(二阶导数)
使用二阶泰勒展开局部近似
一维:
q ( x ) = f ( x k ) + ( x − x k ) f ′ ( x k ) + ( x − x k ) 2 2 f ′ ′ ( x k ) q ′ ( x ) = f ′ ( x k ) + ( x − x k ) f ′ ′ ( x k ) = 0 ⇒ x k + 1 = x k − f ′ ( x k ) f ′ ′ ( x k ) \begin{array}{l}q\left( x\right) =f\left( x_{k}\right) +\left( x-x_{k}\right) f'\left( x_{k}\right) +\dfrac{\left( x-x_{k}\right) ^{2}}{2}f''\left( x_{k}\right) \\ q'\left( x\right) =f'\left( x_{k}\right) +\left( x-x_{k}\right) f''\left( x_{k}\right) =0\\ \Rightarrow x_{k+1}=x_{k}-\dfrac{f'\left( x_{k}\right) }{f''\left( x_{k}\right) }\end{array} q(x)=f(xk)+(x−xk)f′(xk)+2(x−xk)2f′′(xk)q′(x)=f′(xk)+(x−xk)f′′(xk)=0⇒xk+1=xk−f′′(xk)f′(xk)
多维:
q ( x ) = f ( x k ) + ∇ f T ( x k ) ( x − x k ) + 1 2 ( x − x k ) T H ( x k ) ( x − x k ) q ′ ( x ) = ∇ f ( x k ) + H ( x k ) ( x − x k ) = 0 ⇒ x k + 1 = x k − H − 1 ( x k ) ∇ f ( x k ) \begin{array}{l}q\left( x\right) =f\left( x_{k}\right) +\nabla f^{T}\left( x_{k}\right) \left( x-x_{k}\right) +\dfrac{1}{2}\left( x-x_{k}\right) ^{T}H\left( x_{k}\right) \left( x-x_{k}\right) \\ q'\left( x\right) =\nabla f\left( x_{k}\right) +H\left( x_{k}\right) \left( x-x_{k}\right) =0\\ \Rightarrow x_{k+1}=x_{k}-H^{-1}\left( x_{k}\right) \nabla f\left( x_{k}\right) \end{array} q(x)=f(xk)+∇fT(xk)(x−xk)+21(x−xk)TH(xk)(x−xk)q′(x)=∇f(xk)+H(xk)(x−xk)=0⇒xk+1=xk−H−1(xk)∇f(xk)
共轭方向法-二次终止性
共轭方向法就是采用一组共轭方向作为连续搜索方向的优化方法。共轭方向法的推导过程和牛顿法一样,也是先基于二次目标函数,然后推广到一般目标函数的。
子空间扩展定理
设 G G G为 n × n n\times n n×n对称正定矩阵, d 0 , d 1 , ⋯ , d n − 1 d_0,d_1,\cdots,d_{n-1} d0,d1,⋯,dn−1为 G G G的共轭向量组,对于
f ( x ) = 1 2 x T G x + b T x f\left( x\right) =\dfrac{1}{2}x^{T}Gx+b^{T}x f(x)=21xTGx+bTx
由任意 x 0 x_0 x0出发,依次沿直线 x k + λ d k x_k+\lambda d_k xk+λdk作精确线搜索得 λ k ( k = 0 , ⋯ , n − 1 ) \lambda_k(k=0,\cdots,n-1) λk(k=0,⋯,n−1),则
g k T d j = 0 , j = 0 , ⋯ , k − 1 g_k^Td_j=0,j=0,\cdots,k-1 gkTdj=0,j=0,⋯,k−1
其中 g k = G x k + b g_k=Gx_k+b gk=Gxk+b,且 x k x_k xk是 f ( x ) f(x) f(x)在集合
X k = { x ∣ x ∈ R n , x = x 0 + ∑ j = 0 k − 1 α j d j , α j ∈ R , j = 0 , ⋯ , k − 1 } X_{k}=\left\{ x{\mid} x\in \mathbb{R} ^{n},x=x_{0}+\sum ^{k-1}_{j=0}\alpha _{j}d_j\ ,\ \alpha _{j}\in \mathbb{R},j=0,\cdots ,k-1\right\} Xk={x∣x∈Rn,x=x0+j=0∑k−1αjdj , αj∈R,j=0,⋯,k−1}
上的极小点。特别地, x n x_n xn是 f ( x ) f(x) f(x)在 R n \mathbb{R}^n Rn中的极小点。
p r o f : {\bf prof:} prof: 对于定理的第一个结论,由精确线搜索的结果知
λ k = arg min λ f ( x k + λ d k ) ⇒ d f ( x k + λ d k ) d λ ∣ λ = λ k = ∇ f T ( x k + λ k d k ) d k = 0 ⇒ g k + 1 T d k = 0 \lambda _{k}=\arg\min_{\lambda} f\left( x_{k}+\lambda d_{k}\right) \\ \Rightarrow \dfrac{df\left( x_{k}+\lambda d_k\right) }{d\lambda }{\LARGE\mid} _{\lambda=\lambda_ k}=\nabla f^{T}\left( x_{k}+\lambda _{k}d_{k}\right) d_{k}=0 \Rightarrow g_{k+1}^{T}d_{k}=0 λk=argλminf(xk+λdk)⇒dλdf(xk+λdk)∣λ=λk=∇fT(xk+λkdk)dk=0⇒gk+1Tdk=0
注意到 g i = G x i + b x i + 1 − x i = λ i d i g_i=Gx_i+b\quad x_{i+1}-x_i=\lambda_i d_i gi=Gxi+bxi+1−xi=λidi
g k = g j + 1 + ∑ i = j + 1 k − 1 ( g i + 1 − g i ) = g j + 1 + G ∑ i = j + 1 k − 1 ( x i + 1 − x i ) = g j + 1 + G ∑ i = j + 1 k − 1 λ i d i g k T d j = g j + 1 T d j + ∑ i = j + 1 k − 1 α i d i T G d j = 0 \begin{array}{l} g_{k}=g_{j+1}+\sum ^{k-1}_{i=j+1}\left( g_{i+1}-g_{i}\right) =g_{j+1}+G\sum ^{k-1}_{i=j+1}\left( x_{i+1}-x_{i}\right) \\\quad=g_{j+1}+G\sum ^{k-1}_{i=j+1}\lambda _{i}d_{i}\\ g_{k}^{T}d_{j} =g_{j+1}^{T}d_{j}+\sum ^{k-1}_{i=j+1}\alpha _{i}d_i^{T}Gd_{j}=0 \\ \end{array} gk=gj+1+∑i=j+1k−1(gi+1−gi)=gj+1+G∑i=j+1k−1(xi+1−xi)=gj+1+G∑i=j+1k−1λidigkTdj=gj+1Tdj+∑i=j+1k−1αidiTGdj=0
对于定理的第二个结论,只需证明 ∀ x ∈ X k , f ( x ) ≥ f ( x k ) \forall x\in X_{k},f\left( x\right) \geq f\left( x_{k}\right) ∀x∈Xk,f(x)≥f(xk)
注意到
x k = x 0 + ∑ j = 0 k − 1 λ j d j , x = x 0 + ∑ j = 0 k − 1 α j d j , ∀ x ∈ X k x_{k}=x_{0}+\sum ^{k-1}_{j=0}\lambda _jd_j,x=x_{0}+\sum ^{k-1}_{j=0}\alpha_{j}d_j,\forall x\in X_{k} xk=x0+j=0∑k−1λjdj,x=x0+j=0∑k−1αjdj,∀x∈Xk
注意到 G G G的正定性和第一条结论,有
f ( x ) = f ( x k ) + ( x − x k ) T g k + 1 2 ( x − x k ) T G ( x − x k ) ⩾ f ( x k ) + ( x − x k ) T g k = f ( x k ) + ∑ j = 0 k − 1 ( α j − λ j ) d j T g k = f ( x k ) \begin{array}{l} f\left( x\right) =f\left( x_{k}\right) +\left( x-x_{k}\right) ^{T}g_{k}+\dfrac{1}{2}\left( x-x_{k}\right) ^{T}G\left( x-x_{k}\right) \\ \geqslant f\left( x_{k}\right) +\left( x-x_{k}\right) ^{T}g_{k}=f\left( x_{k}\right) +\sum ^{k-1}_{j=0}\left( \alpha _{j}-\lambda _{j}\right) d_{j}^{T}g_{k}=f\left( x_{k}\right) \end{array} f(x)=f(xk)+(x−xk)Tgk+21(x−xk)TG(x−xk)⩾f(xk)+(x−xk)Tgk=f(xk)+∑j=0k−1(αj−λj)djTgk=f(xk)
共轭梯度法
共轭梯度法的基本原理:在寻优过程中利用当前点 x k x_k xk处的梯度向量和前一点 x k − 1 x_{k-1} xk−1处的搜索方向 d k − 1 d_{k-1} dk−1对最速下降方向进行如下修正
d k = − ∇ f ( x k ) + β k d k − 1 d_{k}=-\nabla f(x_k)+\beta_k d_{k-1} dk=−∇f(xk)+βkdk−1
并保证新的搜索方向 d k d_k dk和之前的搜索方向满足共轭关系。
对正定二次函数的共轭梯度法
共轭方向是根据正定二次函数 f ( x ) = 1 2 x T G x + b T x f\left( x\right) =\dfrac{1}{2}x^{T}Gx+b^{T}x f(x)=21xTGx+bTx的梯度来构造的。
取 d 0 = − g 0 d_0=-g_0 d0=−g0。假定已求出关于 G G G共轭的方向 d 0 , d 1 , ⋯ , d k − 1 d_0,d_1,\cdots,d_{k-1} d0,d1,⋯,dk−1,下面求 d k d_k dk,使其与 d 0 , d 1 , ⋯ , d k − 1 d_0,d_1,\cdots,d_{k-1} d0,d1,⋯,dk−1共轭。
由子空间扩展定理知, d k , g k d_k,g_k dk,gk均不在 d 0 , d 1 , ⋯ , d k − 1 d_0,d_1,\cdots,d_{k-1} d0,d1,⋯,dk−1张成的子空间内, g k g_k gk可与 d 0 , d 1 , ⋯ , d k − 1 d_0,d_1,\cdots,d_{k-1} d0,d1,⋯,dk−1张成一个 k + 1 k+1 k+1维子空间,故取 d k d_k dk为 g k , d 0 , d 1 , ⋯ , d k − 1 g_k,d_0,d_1,\cdots,d_{k-1} gk,d0,d1,⋯,dk−1的线性组合,其中 g k g_k gk的系数取为 − 1 -1 −1,则
d k = − g k + ∑ i = 0 k − 1 β i ( k − 1 ) d i d_{k}=-g_{k}+\sum ^{k-1}_{i=0}\beta _{i}^{\left( k-1\right) }d_i dk=−gk+i=0∑k−1βi(k−1)di
确定系数 β 0 ( k − 1 ) , ⋯ , β k − 1 ( k − 1 ) \beta_0^{(k-1)},\cdots,\beta_{k-1}^{(k-1)} β0(k−1),⋯,βk−1(k−1)使得
d k T G d j = 0 , j = 0 , … , k − 1 d_{k}^{T}Gd_j=0,j=0,\ldots ,k-1 dkTGdj=0,j=0,…,k−1
代入得
( − g k + ∑ i = 0 k − 1 β i ( k − 1 ) d i ) T G d j = 0 \left( -g_{k}+\sum ^{k-1}_{i=0}\beta _{i}^{\left( k-1\right) }d_{i}\right) ^{T}Gd_j=0 (−gk+i=0∑k−1βi(k−1)di)TGdj=0
由 d i , d j ( i ≠ j ) d_i,d_j(i\neq j) di,dj(i=j)的共轭性得
β j ( k − 1 ) = g k G d j d i T G d j , j = 0 , … , k − 1 \beta _{j}^{\left( k-1\right) }=\dfrac{g_{k}Gd_j}{d_{i}^{T}Gd_j},\quad j=0,\ldots ,k-1\\ βj(k−1)=diTGdjgkGdj,j=0,…,k−1
下面证明 β ( k − 1 ) j = 0 ( j = 0 , … , k − 2 ) \beta^{(k-1)_j}=0(j=0,\ldots ,k-2) β(k−1)j=0(j=0,…,k−2),从而化简式子
x j + 1 − x j = λ j d j ( λ j > 0 ) , g j = G x j + b λ j g k T G d j = g k T G ( x j + 1 − x j ) = g k T ( g j + 1 − g j ) ∵ g k T g j = 0 , j = 0 , … , k − 1 ∴ g k T ( g j + 1 − g j ) = { 0 , j = 0 , … , k − 2 g k T ( g k − g k − 1 ) , j = k − 1 ⇒ β j ( k − 1 ) = 0 ( j = 0 , … , k − 2 ) ∴ d k = − g k + β k − 1 ( k − 1 ) d k − 1 \begin{array}{l} x_{j+1}-x_{j}=\lambda _{j}d_{j}\left( \lambda j >0\right) ,g_{j}=Gx_{j}+b\\ \lambda _{j}g_{k}^{T}Gd_{j}=g_{k}^{T}G\left( x_{j+1}-x_{j}\right) =g_{k}^{T}\left( g_{j+1}-g_{j}\right) \\ \because g_{k}^{T}g_{j}=0,j=0,\ldots ,k-1\\ \therefore g_{k}^{T}\left( g_{j+1}-g_{j}\right) = \begin{cases}0,&j=0,\ldots ,k-2\\ g_{k}^{T}\left( g_{k}-g_{k-1}\right) ,&j=k-1\end{cases}\\ \Rightarrow \beta _{j}^{\left( k-1\right) }=0\left( j=0,\ldots ,k-2\right) \\ \therefore d_{k}=-g_{k}+\beta _{k-1}^{\left( k-1\right) }d_{k-1}\\ \end{array} xj+1−xj=λjdj(λj>0),gj=Gxj+bλjgkTGdj=gkTG(xj+1−xj)=gkT(gj+1−gj)∵gkTgj=0,j=0,…,k−1∴gkT(gj+1−gj)={0,gkT(gk−gk−1),j=0,…,k−2j=k−1⇒βj(k−1)=0(j=0,…,k−2)∴dk=−gk+βk−1(k−1)dk−1
由精确线搜索的结果,对 β k − 1 ( k − 1 ) \beta _{k-1}^{( k-1)} βk−1(k−1)表达式分子分母同乘 λ k − 1 \lambda_{k-1} λk−1
λ k − 1 d k − 1 T G d k − 1 = d k − 1 T ( g k − g k − 1 ) = − d k T g k − 1 = ( g k − 1 − β k − 2 ( k − 2 ) d k − 2 ) T g k − 1 = g k − 1 T g k − 1 ( k ⩾ 2 ) \begin{array}{l} \lambda _{k-1}d_{k-1}^{T}Gd_{k-1}=d_{k-1}^{T}\left( g_k-g_{k-1}\right) =-d_{k}^{T}g_{k-1}\\ =\left( g_{k-1}-\beta _{k-2}^{\left( k-2\right) }d_{k-2}\right) ^{T}g_{k-1}\\ =g_{k-1}^{T}g_{k-1}\quad (k\geqslant 2)\\ \end{array} λk−1dk−1TGdk−1=dk−1T(gk−gk−1)=−dkTgk−1=(gk−1−βk−2(k−2)dk−2)Tgk−1=gk−1Tgk−1(k⩾2)
对 k = 1 k=1 k=1,有
λ 0 d 0 T G d 0 = d 0 T ( g 1 − g 0 ) = g 0 T g 0 \lambda_0d_0^TGd_0=d_0^T(g_1-g_0)=g_0^Tg_0 λ0d0TGd0=d0T(g1−g0)=g0Tg0
⇒ β k − 1 ( k − 1 ) = g k T ( g k − g k − 1 ) g k − 1 T g k − 1 \Rightarrow \beta _{k-1}^{\left( k-1\right) }=\dfrac{g_{k}^{T}\left( g_{k}-g_{k-1}\right) }{g_{k-1}^{T}g_{k-1}} ⇒βk−1(k−1)=gk−1Tgk−1gkT(gk−gk−1)
共轭梯度方法的性质
考虑正定二次函数
f ( x ) = 1 2 x T G x + b T x f\left( x\right) =\dfrac{1}{2}x^{T}Gx+b^{T}x f(x)=21xTGx+bTx
对任意初始点 x 0 x_0 x0,取 d 0 = − g 0 d_0=-g_0 d0=−g0,采用精确线搜索的共轭梯度法具有二次终止性;对所有 0 ⩽ k ⩽ m , m < n 0\leqslant k\leqslant m,m
共轭方向: d k T G d i = 0 , i = 0 , ⋯ , k − 1 d_k^TGd_i=0,i=0,\cdots,k-1 dkTGdi=0,i=0,⋯,k−1
正交向量: g k T g i = 0 , i = 0 , ⋯ , k − 1 g_k^Tg_i=0,i=0,\cdots,k-1 gkTgi=0,i=0,⋯,k−1
下降性: d k T g k = − g k T g k d^T_k g_k=-g_k^Tg_k dkTgk=−gkTgk
以及
s p a n { g 0 , ⋯ , g k } = s p a n { g 0 , G g 0 , ⋯ , G k g 0 } s p a n { d 0 , ⋯ , d k } = s p a n { g 0 , G g 0 , ⋯ , G k g 0 } {\rm span}\{g_0,\cdots,g_k\}={\rm span}\{g_0,Gg_0,\cdots,G^kg_0\}\\ {\rm span}\{d_0,\cdots,d_k\}={\rm span}\{g_0,Gg_0,\cdots,G^kg_0\} span{g0,⋯,gk}=span{g0,Gg0,⋯,Gkg0}span{d0,⋯,dk}=span{g0,Gg0,⋯,Gkg0}
证明:由 g k T d j = 0 , j = 0 , ⋯ , k − 1 g_k^Td_j=0,j=0,\cdots,k-1 gkTdj=0,j=0,⋯,k−1和 d k = − g k + ∑ i = 0 k − 1 β i ( k − 1 ) d i d_{k}=-g_{k}+\sum ^{k-1}_{i=0}\beta _{i}^{\left( k-1\right) }d_i dk=−gk+∑i=0k−1βi(k−1)di可得
g k T g i = g k T ( − d i + ∑ j = 0 k − 1 β j ( k − 1 ) d j ) = 0 g_{k}^Tg_i=g^T_k(-d_i+\sum ^{k-1}_{j=0}\beta _{j}^{\left( k-1\right) }d_j)=0 gkTgi=gkT(−di+j=0∑k−1βj(k−1)dj)=0
由共轭梯度方法的定义有
d k T g k = ( − g k + β k − 1 d k − 1 ) T g k = − g k T g k < 0 d^T_k g_k=(-g_k+\beta_{k-1}d_{k-1})^Tg_k=-g^T_kg_k<0 dkTgk=(−gk+βk−1dk−1)Tgk=−gkTgk<0
由数学归纳法证明剩余结论,当 k = 0 k=0 k=0时,成立
假设对于 k = j ( 1 ⩽ j < m ) k=j(1\leqslant j
g j ∈ s p a n { g 0 , G g 0 , ⋯ , G j g 0 } d j ∈ s p a n { g 0 , G g 0 , ⋯ , G j g 0 } g_j\in {\rm span}\{g_0,Gg_0,\cdots,G^j g_0\}\\ d_j\in {\rm span}\{g_0,Gg_0,\cdots,G^j g_0\} gj∈span{g0,Gg0,⋯,Gjg0}dj∈span{g0,Gg0,⋯,Gjg0}
由后一式
G d j ∈ s p a n { G g 0 , G 2 g 0 , ⋯ , G j + 1 g 0 } Gd_j\in {\rm span}\{Gg_0,G^2g_0,\cdots,G^{j+1} g_0\} Gdj∈span{Gg0,G2g0,⋯,Gj+1g0}
再由 x j + 1 = x j + λ j d j x_{j+1}=x_j+\lambda_j d_j xj+1=xj+λjdj得 G x j + 1 = G x j + λ j G d j Gx_{j+1}=Gx_j+\lambda_j Gd_j Gxj+1=Gxj+λjGdj,从而 g j + 1 = g j + λ j G d j g_{j+1}=g_j+\lambda_j Gd_j gj+1=gj+λjGdj
这说明 g j + 1 ∈ s p a n { g 0 , G g 0 , ⋯ , G j + 1 g 0 } g_{j+1}\in {\rm span}\{g_0,Gg_0,\cdots,G^{j+1} g_0\} gj+1∈span{g0,Gg0,⋯,Gj+1g0}
由归纳假设知
s p a n { g 0 , ⋯ , g j + 1 } ⊆ s p a n { g 0 , G g 0 , ⋯ , G j + 1 g 0 } {\rm span}\{g_0,\cdots,g_{j+1}\}\subseteq {\rm span}\{g_0,Gg_0,\cdots,G^{j+1}g_0\} span{g0,⋯,gj+1}⊆span{g0,Gg0,⋯,Gj+1g0}
由归纳假设有
G j + 1 g 0 = G ( G j g 0 ) ∈ s p a n { G d 0 , G d 1 , ⋯ , G d j } G^{j+1}g_0=G(G^jg_0)\in {\rm span}\{Gd_0,Gd_1,\cdots,Gd_j\}\\ Gj+1g0=G(Gjg0)∈span{Gd0,Gd1,⋯,Gdj}
由 g i + 1 = g i + λ i G d i g_{i+1}=g_i+\lambda_i Gd_i gi+1=gi+λiGdi得 G d i = g i + 1 − g i λ i ( i = 0 , ⋯ , j ) Gd_i=\dfrac{g_{i+1}-g_i}{\lambda_i}(i=0,\cdots,j) Gdi=λigi+1−gi(i=0,⋯,j),则
G j + 1 g 0 ∈ s p a n { g 0 , ⋯ , g j + 1 } G^{j+1}g_0\in{\rm span}\{g_0,\cdots,g_{j+1}\} Gj+1g0∈span{g0,⋯,gj+1}
由上式和归纳假设知
s p a n { g 0 , G g 0 , ⋯ , G j + 1 g 0 } ⊆ s p a n { g 0 , ⋯ , g j + 1 } ⟹ s p a n { g 0 , G g 0 , ⋯ , G j + 1 g 0 } = s p a n { g 0 , ⋯ , g j + 1 } {\rm span}\{g_0,Gg_0,\cdots,G^{j+1}g_0\}\subseteq{\rm span}\{g_0,\cdots,g_{j+1}\}\\ \implies {\rm span}\{g_0,Gg_0,\cdots,G^{j+1}g_0\}={\rm span}\{g_0,\cdots,g_{j+1}\} span{g0,Gg0,⋯,Gj+1g0}⊆span{g0,⋯,gj+1}⟹span{g0,Gg0,⋯,Gj+1g0}=span{g0,⋯,gj+1}
由 d j + 1 = − g j + 1 + β j d j d_{j+1}=-g_{j+1}+\beta_j d_j dj+1=−gj+1+βjdj和归纳假设有
s p a n { d 0 , ⋯ , d j , d j + 1 } = s p a n { d 0 , ⋯ , d j , g j + 1 } = s p a n { g 0 , ⋯ , g j , g j + 1 } = s p a n { g 0 , ⋯ , G j g 0 , G j + 1 g 0 } {\rm span}\{d_0,\cdots,d_j,d_{j+1}\}={\rm span}\{d_0,\cdots,d_j,g_{j+1}\}\\ ={\rm span}\{g_0,\cdots,g_j,g_{j+1}\}={\rm span}\{g_0,\cdots,G^jg_0,G^{j+1}g_0\} span{d0,⋯,dj,dj+1}=span{d0,⋯,dj,gj+1}=span{g0,⋯,gj,gj+1}=span{g0,⋯,Gjg0,Gj+1g0}
拟牛顿法
利用一阶导数信息来逼近二阶Hessian矩阵信息,则称为拟牛顿法。
f ( x ) ≈ f ( x k + 1 ) + g k + 1 T ( x − x k + 1 ) + 1 2 ( x − x k + 1 ) T H k + 1 ( x − x k + 1 ) g ( x ) ≈ g k + 1 + H k + 1 ( x − x k + 1 ) = 0 \begin{array}{l}f\left( x\right) \approx f\left( x_{k+1}\right) +g_{k+1}^{T} \left( x-x_{k+1}\right) +\dfrac{1}{2}\left( x-x_{k+1}\right) ^{T}H_{k+1} \left( x-x_{k+1}\right) \\ g\left( x\right) \approx g_{k+1} +H_{k+1} \left( x-x_{k+1}\right) =0\\ \end{array} f(x)≈f(xk+1)+gk+1T(x−xk+1)+21(x−xk+1)THk+1(x−xk+1)g(x)≈gk+1+Hk+1(x−xk+1)=0
令 x = x k , s k = x k + 1 − x k , y k = g k + 1 − g k x=x_k,s_k=x_{k+1}-x_{k},y_k=g_{k+1}-g_k x=xk,sk=xk+1−xk,yk=gk+1−gk,可得 H k + 1 − 1 y k ≈ s k → G k + 1 y k = s k H_{k+1}^{-1}y_k\approx s_k\to G_{k+1}y_k=s_k Hk+1−1yk≈sk→Gk+1yk=sk(拟牛顿方程),也可用下述公式 B k + 1 s k = y k B_{k+1}s_k=y_k Bk+1sk=yk表示。通过求解 y k y_k yk获得下次迭代的方向。
变尺度法的基本思想:利用尺度矩阵近似Hesse矩阵的逆矩阵,避免了求Hesse矩阵逆矩阵的计算,通过不断校正更新,使得尺度矩阵逼近Hesse矩阵的逆矩阵。
- 对于凸二次函数,寻优过程中如果都使用精确一维搜索方法获得最佳步长,则下降方向关于H共轭
DFP方法
- 初始化:给定 x 0 ∈ R n , H 0 ∈ R n × n x_0\in R^n,H_0\in R^{n\times n} x0∈Rn,H0∈Rn×n为对称正定矩阵, ε > 0 , k = 0 \varepsilon > 0,k=0 ε>0,k=0
- 第k步迭代:
- 若 ∥ g k ∥ ⩽ ε \Vert{g_k}\Vert\leqslant \varepsilon ∥gk∥⩽ε,终止
- 计算 d k = − H k g k d_k=-H_k g_k dk=−Hkgk
- 计算步长 λ k \lambda_k λk
- s k = λ k d k , x k + 1 = x k + s k , y k = g k + 1 − g k , H k + 1 = H k + s k s k T s k T y k − H k y k y k T H k y k T H k y k s_k=\lambda_k d_k,x_{k+1}=x_k+s_k,y_k=g_{k+1}-g_k,H_{k+1}=H_k+\dfrac{s_k s_k^T}{s^T_k y_k}-\dfrac{H_k y_k y_k^T H_k}{y_k^T H_k y_k} sk=λkdk,xk+1=xk+sk,yk=gk+1−gk,Hk+1=Hk+skTykskskT−ykTHkykHkykykTHk
- k + + k++ k++
BFGS方法
d k = − B k g k B k + 1 = B k + y k y k T y k T s k − B k s k s k T B k s k T B k s k d_k=-B_k g_k\\ B_{k+1}=B_k+\dfrac{y_k y_k^T}{y^T_k s_k}-\dfrac{B_k s_k s_k^T B_k}{s_k^T B_k s_k} dk=−BkgkBk+1=Bk+ykTskykykT−skTBkskBkskskTBk
二次终止性
在非线性目标函数中,正定二次函数具有相当好的性质,这类函数简单、光滑、具有唯一极小点.另外,在极小点附近,一般函数可以用正定二次函数很好地近似.因此能否有效地求得正定二次函数的极小点,是检验一算法好坏的标准之一,对于一个算法,如果它对任意正定二次函数,从任意初始点出发,可以经有限步迭代求得极小点,我就说该算法具有二次终止性.在下面的章节中,我们会讨论具体方法的二次终止性.
