Frenet坐标系与Cartesian坐标系互转（一）：公式推导

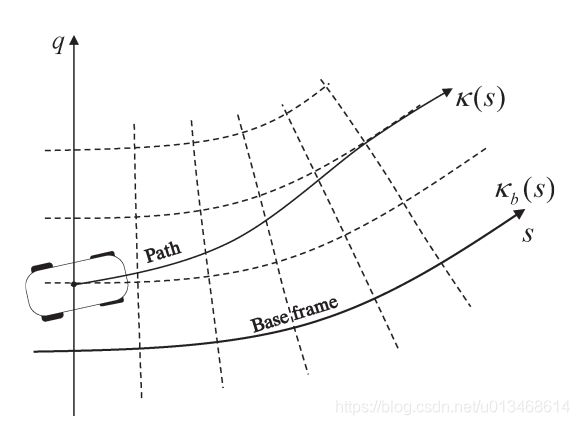
Frenet坐标系在无人驾驶领域被普遍使用，特别是在城市、高速等道路交通环境下无人驾驶的路径规划系统中。Frenet坐标系使用道路的中心线作为Base frame，使用参考线的切线向量和法线向量建立坐标系。相比笛卡尔坐标系，Frenet坐标系简化了路径规划问题。网上关于Frenet坐标系的博客或资料很多，此处不再赘述。本文先给出简单的转换公式推导过程，然后给出三对Frenet坐标系与Cartesian坐标系互转的python代码与使用示例方便自己查阅使用。详细推导参见博客Apollo项目坐标系研究。note：下图中Frenet的q坐标轴也可以用d或l表示。

一、 Frenet坐标系与Cartesian坐标系的转换公式简单推导

1.1 Frenet公式

下图显示了一条3D空间中一条连续可微的曲线K，P为曲线K上的一个点，黄色平面为曲线K在点P处的运动平面。$T$为曲线K在点P处的切向量，$N$为K在P处的法向量（$N$与$T$在同一运动平面）,$B$为曲线K在P处的副法向量（$B$垂直于运动平面）。

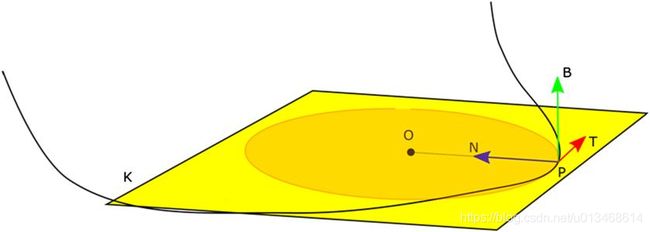
有Frenet公式：
$$\{\begin{array}{cc}\frac{dT}{ds}=& kN\\ \frac{dN}{ds}=& -kT+\tau B\\ \frac{dB}{ds}=& -\tau N\end{array}$$

其中，$\frac{d}{ds}$表示某一方向向量对弧长$s$的导数，$k$为曲率（ curvature），$\tau$为挠率（ torsion）。

• 曲率：曲线不能形成一条直线的度量值，曲率越趋于0，则曲线越趋近于直线；
• 挠率：是曲线不能形成在同一平面内运动曲线的度量值，挠率越趋于0，则曲线越趋近于在同一平面内运动。

在大地表面，局部路面可看作一个平面，对于无人驾驶路径规划应用，挠率可设定为0。从而Frenet公式进一步简化为：
$$\{\begin{array}{cc}\frac{dT}{ds}=& kN\\ \frac{dN}{ds}=& -kT\end{array}\text{\hspace{1em}(1)}$$

1.2 简单推导过程

引博客Apollo项目坐标系研究中的图如下：

Frenet坐标系：$[s,\dot{s},\ddot{s},l,\dot{l},\ddot{l},l^{\prime },l^{\prime \prime }]$，Cartesian坐标系：$[x,v_x,a_a,{\theta }_x,k_x]$，释义如下：

• $s$：Frenet纵坐标；
• $\dot{s}=\frac{ds}{dt}$：Frenet纵坐标对时间的导数，也即沿base frame的速度；
• $\ddot{s}=\frac{d\dot{s}}{dt}$：沿base frame的加速度；
• $l$：Frenet横坐标；
• $\dot{l}=\frac{dl}{dt}$：Frenet横向速度；
• $\ddot{l}=\frac{d\dot{l}}{dt}$：Frenet横向加速度；
• $l^{\prime }=\frac{dl}{ds}$：Frenet横向坐标对纵向坐标的导数；
• $l^{\prime \prime }=\frac{d{l}^{\prime }}{ds}$：Frenet横向坐标对纵向坐标的二阶导；
• $x$：为对应Cartesian坐标系下的坐标，是一个向量；
• ${\theta }_x$：Cartesian坐标系下的朝向；
• $k_x=\frac{d{\theta }_x}{ds}$：曲率；
• $v_x=||\dot{x}|{|}_2$：Cartesian坐标系下的线速度（无方向，无正负）；
• $a_x=\frac{d{v}_x}{dt}$：Cartesian坐标系下的加速度；

已知$x=[x_x,y_x]$推导$[s,l]$

• 求$s$
  首先，找到曲线上离$[x_x,y_x]$最近的参考点$r=[x_r,y_r]$，该参考点处的$s$即为$[x_x,y_x]$在Frenet坐标系下的$s$。

• 求$l$
  $x,r$分别为参考点与待转换点在Cartesian坐标系下的向量，我们有$x=r+l{N}_r$，变换可得：
  $$l=(x-r{)}^T{N}_r=||x-r|{|}_2\cos ({\theta }_{x-r}-({\theta }_r+\frac{\pi }{2}))=||x-r|{|}_2(\sin ({\theta }_{x-r})\cos ({\theta }_r)-\cos ({\theta }_{x-r})\sin ({\theta }_r))$$

备注：上式中，${\theta }_{x-r}$为向量$x-r$的方向角度，${\theta }_r+\frac{\pi }{2}$为单位向量$N_r$的方向角度（对比上一张图可知），则上式可利用向量点乘公式$a\times b=|a||b|\cos \theta$得到。此处，$\theta$为向量$a$与向量$b$之间的夹角。

假定$x=(x_x,y_x),r=(x_r,y_r)$，则$||x-r|{|}_2=\sqrt{(x_x-x_r{)}^2+(y_x-y_r{)}^2}$

在Frenet坐标系下，每个点到base frame上参考点的向量都与该参考点的法向量$N$同向或反向，因此，$\sin ({\theta }_{x-r})\cos ({\theta }_r)-\cos ({\theta }_{x-r})\sin ({\theta }_r)=1或-1$。${\theta }_{x-r}$为向量$x-r$的角度，因此，$\frac{\sin ({\theta }_{x-r})}{\cos ({\theta }_{x-r})}=\frac{y_x-y_r}{x_x-x_r}$。可以根据$\sqrt{(x_x-x_r{)}^2+(y_x-y_r{)}^2}$来确定$l$的绝对取值，$(y_x-y_r)\cos ({\theta }_r)-(x_x-x_r)\sin ({\theta }_r)$的正负来确定$l$的正负号，公式如下：

$$l=sign\left((y_x-y_r)\cos ({\theta }_r)-(x_x-x_r)\sin ({\theta }_r)\right)\sqrt{(x_x-x_r{)}^2+(y_x-y_r{)}^2}\text{\hspace{1em}(2)}$$

已知$x=[x_x,y_x],{\theta }_x,v_x$推导$[s,l,\dot{s},\dot{l},l^{\prime }]$

• 求$\dot{l}$（根据$v_x$与$\dot{s}$定义，有$\dot{r}=\dot{s}{T}_r$和$\dot{x}=v_x{T}_x$）
  由$x$与$r$的关系$x=r+l{N}_r$，可得$l=(x-r{)}^T{N}_r$，两边对时间$t$求导得如下等式:
  $$\begin{gathered} \dot{l}=(\dot{x}-\dot{r}{)}^T{N}_r+(x-r{)}^T\dot{N_r} \\ =v_x{T_x}^T{N}_r-\dot{s}{T_r}^T{N}_r+l{N_r}^T\dot{N_r} \end{gathered}$$

由Frenet公式（见上式(1)）有${N_r}^{\prime }=\frac{d{N}_r}{ds}=-k_r{T}_r$，于是有$\dot{N_r}=\frac{ds}{dt}\frac{d{N}_r}{ds}=-k_r\dot{s}{T}_r$，代入上式可得：

$$\dot{l}=v_x{T_x}^T{N}_r-\dot{s}{T_r}^T{N}_r-l\dot{s}{k}_r{N_r}^T{T}_r$$

由于$N_r$与$T_r$正交$\Rightarrow {N_r}^T{T}_r={T_r}^T{N}_r=0$，${T_x}^T{N}_r=\cos ({\theta }_x-{\theta }_r-\frac{\pi }{2})=\sin ({\theta }_x-{\theta }_r)$,代入上式得：
$$\dot{l}=v_x\sin ({\theta }_x-{\theta }_r)\text{\hspace{1em}(3)}$$

• 求$\dot{s}$
  由$x$与$r$的关系$x=r+l{N}_r$，对等式两边求导可得：$v_x{T}_x=\dot{s}{T}_r+\dot{l}{N}_r-\dot{s}{k}_{r}l{T}_r$

上式两边左乘$T_r$得到$v_x\cos ({\theta }_x-{\theta }_r)=\dot{s}(1-k_{r}l)$，整理可得：
$$\dot{s}=\frac{v_x\cos ({\theta }_x-{\theta }_r)}{1-k_{r}l}\text{\hspace{1em}(4)}$$

• 求$l^{\prime }$

$l^{\prime }=\frac{dl}{ds}=\frac{\dot{l}}{\dot{s}}$ ，将$\dot{l}$与$\dot{s}$代入得：

$$l^{\prime }=(1-k_{r}l)\tan ({\theta }_x-{\theta }_r)\text{\hspace{1em}(5)}$$

已知$x=[x_x,y_x],{\theta }_x,v_x,a_x,k_x$推导$[s,l,\dot{s},l^{\prime },\ddot{s},l^{\prime \prime }]$

• 求$l^{\prime \prime }$

由$l^{\prime }=(1-k_{r}l)\tan ({\theta }_x-{\theta }_r)$，可得$l^{\prime \prime }=\frac{d{l}^{\prime }}{ds}=(1-k_{r}l{)}^{\prime }\tan ({\theta }_x-{\theta }_r)+(1-k_{r}l)\frac{({\theta }_x-{\theta }_r{)}^{\prime }}{{\cos }^2({\theta }_x-{\theta }_r)}$

假定$s_x$为为车辆当前轨迹$x$的弧长，有：
$\frac{d}{ds}=\frac{d{s}_x}{dt}\frac{dt}{ds}\frac{d}{d{s}_x}=\frac{v_x}{\dot{s}}\frac{d}{d{s}_x}=\frac{1-k_{r}l}{\cos ({\theta }_x-{\theta }_r)}\frac{d}{d{s}_x}$

又有曲率:$k_r=\frac{d{\theta }_r}{ds}$,$k_x=\frac{d{\theta }_x}{d{s}_x}$

故：$l^{\prime \prime }=\frac{d{l}^{\prime }}{ds}=-(k_r^{\prime }l+k_r{l}^{\prime })\tan ({\theta }_x-{\theta }_r)+\frac{(1-k_{r}l)}{{\cos }^2({\theta }_x-{\theta }_r)}(\frac{d{\theta }_x}{ds}-\frac{d{\theta }_r}{ds})$

由于:$\frac{d{\theta }_x}{ds}=\frac{1-k_{r}l}{\cos ({\theta }_x-{\theta }_r)}\frac{d{\theta }_x}{d{s}_x}=\frac{1-k_{r}l}{\cos ({\theta }_x-{\theta }_r)}{k}_x$
综上可得：

$$l^{\prime \prime }=-(k_r^{\prime }l+k_r{l}^{\prime })\tan ({\theta }_x-{\theta }_r)+\frac{(1-k_{r}l)}{{\cos }^2({\theta }_x-{\theta }_r)}(\frac{1-k_{r}l}{\cos ({\theta }_x-{\theta }_r)}{k}_x-k_r)\text{\hspace{1em}(6)}$$

$a_x=\frac{d{v}_x}{dt}=\ddot{s}\frac{1-k_{r}l}{\cos ({\theta }_x-{\theta }_r)}+\frac{{\dot{s}}^2}{\cos ({\theta }_x-{\theta }_r)}\left[l^{\prime }(k_x\frac{1-k_{r}l}{\cos ({\theta }_x-{\theta }_r)}-k_r)-(k_r^{\prime }l+k_r{l}^{\prime })\right]$

$$\ddot{s}=\frac{a_x\cos ({\theta }_x-{\theta }_r)-{\dot{s}}^2\left[l^{\prime }(k_x\frac{1-k_{r}l}{\cos ({\theta }_x-{\theta }_r)}-k_r)-(k_r^{\prime }l+k_r{l}^{\prime })\right]}{1-k_{r}l}\text{\hspace{1em}(7)}$$

综合以上可得转换公式

• Cartesian转 Frenet
  $$\{\begin{array}{cc}s=& s_r\\ \dot{s}=& \frac{v_x\cos ({\theta }_x-{\theta }_r)}{1-k_{r}l}\\ \ddot{s}=& \frac{a_x\cos ({\theta }_x-{\theta }_r)-{\dot{s}}^2\left[l^{\prime }(k_x\frac{1-k_{r}l}{\cos ({\theta }_x-{\theta }_r)}-k_r)-(k_r^{\prime }l+k_r{l}^{\prime })\right]}{1-k_{r}l}\\ l=& sign\left((y_x-y_r)\cos ({\theta }_r)-(x_x-x_r)\sin ({\theta }_r)\right)\sqrt{(x_x-x_r{)}^2+(y_x-y_r{)}^2}\\ l^{\prime }=& (1-k_{r}l)\tan ({\theta }_x-{\theta }_r)\\ l^{\prime \prime }=& -(k_r^{\prime }l+k_r{l}^{\prime })\tan ({\theta }_x-{\theta }_r)+\frac{(1-k_{r}l)}{{\cos }^2({\theta }_x-{\theta }_r)}(\frac{1-k_{r}l}{\cos ({\theta }_x-{\theta }_r)}{k}_x-k_r)\end{array}\text{\hspace{1em}(8)}$$

• Frenet转Cartesian
  $$\{\begin{array}{cc}{x}_x=& x_r-l\sin ({\theta }_r)\\ y_x=& y_r+l\cos ({\theta }_r)\\ {\theta }_x=& \arctan (\frac{l^{\prime }}{1-k_{r}l})+{\theta }_r\in [-\pi ,\pi ]\\ v_x=& \sqrt{[\dot{s}(1-k_{r}l){]}^2+(\dot{s}{l}^{\prime }{)}^2}\\ a_x=& \ddot{s}\frac{1-k_{r}l}{\cos ({\theta }_x-{\theta }_r)}+\frac{{\dot{s}}^2}{\cos ({\theta }_x-{\theta }_r)}\left[l^{\prime }(k_x\frac{1-k_{r}l}{\cos ({\theta }_x-{\theta }_r)}-k_r)-(k_r^{\prime }l+k_r{l}^{\prime })\right]\\ k_x=& ((l^{\prime \prime }+(k_r^{\prime }l+k_r{l}^{\prime })\tan ({\theta }_x-{\theta }_r))\frac{{\cos }^2({\theta }_x-{\theta }_r)}{1-k_{r}l}+k_r)\frac{\cos ({\theta }_x-{\theta }_r)}{1-k_{r}l}\end{array}\text{\hspace{1em}(9)}$$

cartesian转Frenet一般计算步骤

问题：已知$(x_x,y_x,{\theta }_x,v_x,a_x,k_x),(s_r,x_r,y_r,{\theta }_r,k_r,k_r^{\prime }),$求$s,\dot{s},\ddot{s},l,l^{\prime },l^{\prime \prime }$

step 1：计算$d_x=x_x-x_r,d_y=y_x-y_r,d_{\theta }={\theta }_x-{\theta }_r$;
step 2：计算$C_{drdx}=d_y\cos ({\theta }_r)-d_x\sin ({\theta }_r)$;
step 3：计算$l=sign(C_{d}rdx)\sqrt{d_x^2+d_y^2}$;
step 4：计算$C_{1-k_{r}l}=1-k_{r}l$;
step 5：计算$l^{\prime }=C_{1-k_{r}l}\tan (d_{\theta })$;
step 6：计算$C_{k_r{l}^{\prime }}=k_r^{\prime }l+k_r{l}^{\prime }$;
step 7：计算$l^{\prime \prime }=-C_{k_r{l}^{\prime }}\tan (d_{\theta })+\frac{C_{1-k_{r}l}}{\cos (d_{\theta })}(\frac{k_x{C}_{1-k_{r}l}}{\cos (d_{\theta })}-k_r)$;
step 8：计算$s=s_r$;
step 9：计算$\dot{s}=\frac{v_x\cos (d_{\theta })}{C_{1-k_{r}l}}$;
step 10：计算$C_{d_{\theta }^{\prime }}=\frac{C_{1-k_{r}l}}{k_x\cos (d_{\theta })}-k_r$;
step 11：计算$\ddot{s}=\frac{a_x\cos (d_{\theta })-{\dot{s}}^2(l^{\prime }{C}_{d_{\theta }^{\prime }}-C_{k_r{l}^{\prime }})}{C_{1-k_{r}l}}$

---

Frenet坐标系与Cartesian坐标系互转（二）：Python代码函数实现

Frenet坐标系与Cartesian坐标系互转（三）：应用示例

---

END
by windSeS
first update 2020.9.23
modified at 2022.5.19