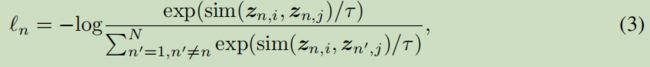【论文翻译】Graph Contrastive Learning with Augmentations

Graph Contrastive Learning with Augmentations

目录

Graph Contrastive Learning with Augmentations

摘要

1，引言

2，相关工作

3，方法论

3.1，图形的数据增强

3.2，图对比学习

4，数据增强在图形对比学习中的作用

4.1，数据指导是至关重要的。构成指导的好处。

4.2，有效图形增强的类型、范围和模式

4.3，与“更硬”的任务不同，过于简单的对比任务并没有帮助。

5，与最先进的方法的比较

6，结论

References

---

摘要

对于当前的图神经网络(GNNs)来说，在图结构数据上的可通用、可转移和鲁棒的表示学习仍然是一个挑战。与用于图像数据的卷积神经网络(CNNs)开发的技术不同，自我监督学习和预训练的探索较少。在本文中，我们提出了一个图对比学习(学习图数据无监督表示框架的GraphCL)。我们首先设计了四种类型的图扩充来合并各种先验。然后，我们系统地研究了在四种不同设置下的不同组合的图增强对多个数据集的影响：半监督、无监督和迁移学习以及对抗性攻击。结果表明，即使不调优增强范围，也不使用复杂的GNN架构，我们的Graph框架l框架也可以产生类似或更好的通用性、可转移性和鲁棒性的图表示。我们还研究了参数化图增强范围和模式的影响，并在初步实验中观察到进一步的性能提高。我们的代码在：https://github.com/Shen-Lab/GraphCL.

1，引言

图神经网络(GNNs)[1,2,3]遵循邻域聚合方案，在图结构数据中越来越受欢迎。许多GNN的变体已经被提出，以在基于图的任务中实现最先进的性能，如节点或链接分类[1,2,4,5,6]、链接预测[7]和图分类[8,3]。有趣的是，在大多数图级任务的场景中，gnn是在监督下进行端到端训练的。对于gnn，很少探索（自监督）预训练（除了[9]），这是一种通常用于训练遭受梯度消失/爆炸[10,11]的深度架构的规则技术。这一有趣现象背后的原因可能是，大多数被研究的图数据集，如图[12]所示，往往规模有限，gnn通常具有浅层的架构，以避免过度平滑[13]或“信息丢失”[14]。

然而，我们认为探索GNN的训练前方案的必要性。对于图形数据集来说，具有特定任务的标签可能非常稀缺（例如，通过湿实验室实验进行的生物学和化学标签通常需要资源和时间）[15,9]，而预训练可以是一种很有前途的技术来缓解这个问题，就像它在卷积神经网络(CNNs)[16,17,18]中所做的那样。至于缺乏GNN预训练的推测原因：首先，现实世界的图数据可能是巨大的，甚至基准数据集最近得到越来越大的[12,19]；其次，即使是浅层模型，预训练也可以在一个“更好的”围绕一个局部最小值与更好的泛化[11]相关吸引盘中初始化参数。因此，我们强调了GNN预训练的意义。

与图像的CNNs相比，为图结构数据设计GNN预训练方案存在着独特的挑战。与图像中的几何信息不同，不同上下文的丰富的结构化信息存在于图数据[20,21]中，因为图是具有不同性质的原始数据（例如由化学键原子组成的分子和与社会互动的人的网络）的抽象表示。因此，设计一个一般有益于下游任务的GNN预训练方案是不同的。图级任务的一种朴素的GNN预训练方案是重建顶点邻接信息(例如，网络嵌入中的GAE[22]和GraphSAGE[23])。这个方案可能非常有限(如[20]和我们的Sec所示。5)因为它过度强调接近，这并不总是有益于[20]，并可能会损害结构信息[24]。因此，需要一个精心设计的预训练框架来捕获图结构数据中的高度异构的信息。

最近，在视觉表征学习中，对比学习重新引起了[25,26,27,18,28]的兴趣。[29,30,31,32]使用手工制作的借口任务进行自我监督，它依赖于启发式方法来设计，因此可能会限制学习到的表示的通用性。相比之下，对比学习的目的是通过在不同的增强视图下最大化特征一致性来学习表示，利用数据或任务特定的增强[33]来注入所需的特征不变性。如果扩展到训练前的gcn，该框架可能会克服上述基于接近性的训练前方法[22,23,34,35,36,37,38,39]的局限性。然而，直接应用于视觉表示学习之外并不简单，它需要对图形表示学习进行重大扩展，这导致了我们下面的创新。

贡献：在本文中，我们开发了与增强GNN预训练的对比学习，以解决图中数据异质性的挑战。(i)由于数据增强是约束学习的先决条件，但在图数据[40]中没有得到充分的探索，我们首先设计了四种类型的图数据增强，每一种都施加了图数据的某些先验，并根据范围和模式进行参数化。(ii)利用它们来获得相关视图，我们为GNN的预训练提出了一种新的图对比学习框架(GraphCL)，以便可以为不同的图结构数据学习对特定扰动不变的表示。此外，我们证明了GraphCL实际上执行互信息最大化，并且GraphCL和最近提出的对比学习方法之间存在联系，我们证明了GraphCL可以重写为一个通用框架，统一图结构数据上广泛的对比学习方法。(iii)进行系统研究，评估在不同类型的数据集上对比不同增强的性能，揭示性能的基本原理，并为特定数据集采用该框架提供指导。(iv)实验表明，GraphCL在半监督学习、无监督表示学习和迁移学习的设置下取得了最先进的性能。此外，它还增强了对常见对抗性攻击的鲁棒性。

2，相关工作

图神经网络。近年来，图神经网络(GNNs)[1,2,3]已成为一种很有前途的分析图结构数据的方法。它们遵循一个迭代的邻域聚合（或消息传递）方案来捕获节点邻域内的结构信息。设

表示无向图，以X∈R|V|×N为特征矩阵，其中

为节点vn∈V的N维属性向量。考虑到k层GNNf（·），第k层的传播表示为：

其中h(k)n是在第k层与h(0)n=xn的嵌入，N(n）是与vn相邻的顶点，

是GNN层的分量函数。在k层传播后，通过读出函数将G的输出嵌入总结为层嵌入。然后采用多层感知器(MLP)进行图级下游任务（分类或回归）：

各种gnn已经被提出为[1,2,3]，在图形任务中实现了最先进的性能。

图形数据增强。对图结构数据的增强仍未得到充分探索，目前还有一些工作，但需要高昂的额外计算成本[40]。传统的自训练方法[40,13]利用训练后的模型对未标注的数据进行注释；[41]提出在对抗性学习设置中训练一个生成器-分类器网络来生成假节点；而[42,43]在图结构上对节点特征产生对抗性扰动。

GNN预训练。虽然（自监督）预训练是卷积神经网络(CNNs)[16,17,18]的一种常见而有效的方案，但它在GNNs中很少被探索。一个例外的[9]仅限于研究迁移学习环境中的训练前策略，我们认为，预先训练的GNN不容易传输，因为图结构数据源来自不同的领域。在迁移过程中，训练前和下游任务都需要大量的领域知识，否则可能会导致负转移[9,44]。

对比学习。对比学习的主要思想是使表示在适当的转换下彼此一致，这引起了最近对视觉表示学习[45,25,26,27,18]的兴趣激增。另外，对于图数据，试图重建顶点[22,23]邻接信息的传统方法可以被视为一种“局部对比”，同时以结构信息[24]为代价过度强调信息的接近。在[46,47]的激励下，[24,21,48]建议在局部和全局表示之间进行对比学习，以更好地捕获结构信息。然而，图对比学习还没有像[27,18]那样从强制扰动不变性的角度进行探索。

3，方法论

3.1，图形的数据增强

数据增强的目的是通过应用某些特定的转换，在不影响语义标签的情况下创建新的和现实合理的数据。除了一些计算成本昂贵的图外，它仍然没有被探索之中(见Sec。 2).我们关注图级的增强。在M图数据集中的图

，我们表示了满足：

的增强图Gˆ，其中q(·|G)是基于原始图的增强分布，原始图是预定义的，表示数据分布的人类先验。例如，对于图像分类，旋转和裁剪的应用对先验进行编码，即人们将从旋转图像或其局部补丁[49,50]中获得相同的基于分类的语义知识。

说到图表，同样的精神也是可以遵循的。然而，正如Sec中所述的一个挑战。1是图形数据集是从不同的字段中提取的，因此可能没有像图像那样普遍适当的数据增强。换句话说，对于不同类别的图形数据集，一些数据可能比其他数据更需要增强。我们主要关注三类：生化分子（如化合物、蛋白质）[9]、社交网络[1]和图像超像素图[12]。接下来，我们提出了图结构数据的四种一般数据增强，并讨论了它们引入的直观先验。

节点下降。给定图G，节点丢弃将随机丢弃顶点的某些部分及其连接。它强制执行的基本先验是，顶点的缺失部分并不影响g的语义意义。每个节点的下降概率都遵循一个默认的i.i.d.均匀分布（或任何其他分布）。

边缘扰动。它会通过随机添加或下降一定比例的边来干扰G中的连通性。说明G的语义意义对边缘连接模式方差具有一定的鲁棒性。我们也关注了一个i.i.d.增减每条边的均匀分布。

属性掩蔽。属性掩蔽提示模型使用它们的上下文信息来恢复掩蔽的顶点属性，即剩余的属性。基本的假设是，缺少部分顶点属性对模型的预测没有太大影响。

子图。这一个使用随机游走从G中抽取一个子图(算法总结在附录a中)。它假设G的语义可以大量地保留在其（部分）局部结构中。

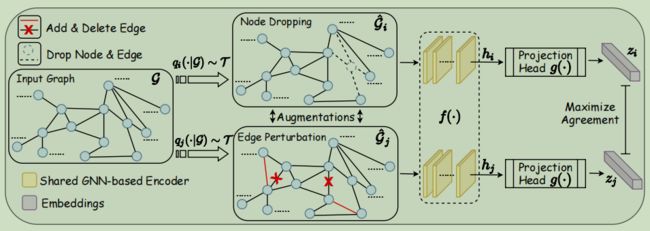
图1：一个图形对比学习的框架。从一个增强池T中采样两个图增强qi(·|G)和qj(·|G)，并应用于输入图G。训练一个共享的基于gnn的编码器f（·）和一个投影头g（·），通过对比损失最大限度地提高表示zi和zj之间的一致性。

默认的增强（下降、扰动、掩蔽和子图）比率设置为0.2。

3.2，图对比学习

受最近视觉表征学习的对比学习发展的激励(见Sec.2)，我们提出了一个图对比学习框架(GraphCL)用于（自我监督）预训练。如图1所示，在图对比学习中，预训练是通过在潜在空间中的对比损失来最大化同一图的两个增广视图之间的一致性来进行的。该框架包括以下四个主要组件：

1. 图形数据增强。给定的图G经过图数据扩充，得到两个相关视图Gˆi、Gˆj作为正对，其中分别为Gˆi∼qi(·|G)，Gˆj∼qj(·|G)。对于图形数据集的不同领域，如何战略性地选择数据增强很重要(Sec.4)。

2. 基于gnn的编码器。一个基于gnn的编码器f（·）（在（2）中定义）提取图级表示向量hi，hj，用于增强图Gˆi，Gˆj。图对比学习对GNN体系结构不应用任何约束。

3. 投影头。一个名为投影头的非线性变换g（·）将增强表示映射到另一个潜在空间，在那里计算对比损失，正如[18]中所提倡的那样。在图对比学习中，应用双层感知器(MLP)得到zi、zj。

4. 对比损失函数。定义了一个对比损失函数L（·），以强制最大限度地提高正对zi、zj与负对之间的一致性。这里我们利用归一化的温度尺度交叉熵损失(NT-Xent)[51,25,52]。

在GNN预训练过程中，对N个图进行随机采样并通过对比学习进行处理，得到2N个增广图和相应的对比损失进行优化，我们将zi、zj重新标注为

。负对不是显式采样的，而是从与[53,18]中相同的小批中的其他N−1增广图中生成的。将第n个图的余弦相似度函数表示为

，第n个图的NT-Xent被定义为：

其中，τ表示温度参数。最终损失计算小批中所有正对。附录A总结了所提出的图对比学习。

讨论。我们首先证明了GraphCL可以看作是两种增强图的潜在表示之间交互信息最大化的一种方法。完整的推导在附录F中，损失表重写如下：

上述损失本质上最大限度地提高了高=f1(Gˆi)、hj=f2(Gˆj)之间的互信息的下界，即(f1、Gˆi)、(f2、Gˆj)的组成决定了我们所期望的图形视图。此外，我们将GraphCL和最近提出的对比学习方法之间建立联系，我们证明了通过重新解释（4），GraphCL可以作为一个通用框架来统一图结构数据上的广泛的对比学习方法。在我们的实现中，我们选择f1=f2并通过数据增强生成Gˆi，Gˆj，而随着各种组合的选择，（4）实例化作为其他特定的对比学习算法，包括[54,55,56,21,57,58,59]，也如附录F所示。

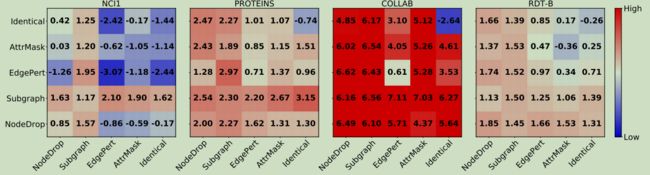
图2：在四个数据集：NCI1, PROTEINS, COLLAB和RDT-B下，与从头开始的训练相比，半监督学习精度提高（%）。配对“相同”表示对比学习的无增强基线，其中正对减少，负对由两个非增强图组成。更温暖的颜色表示更好的性能提高。四个数据集的基线从头训练精度分别为60.72%、70.40%、57.46%、86.63%。

4，数据增强在图形对比学习中的作用

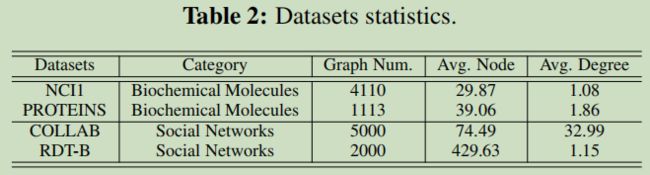
在本节中，我们将评估并合理化GraphCL框架中图形结构数据的数据增强的作用。应用了不同的增强类型对，如图2所示。到三类图数据集(表2，我们在附录C中留下了关于超像素图的讨论)。实验在半监督设置下进行，遵循预训练和微调方法[18]。详细的设置见附录B。

4.1，数据指导是至关重要的。构成指导的好处。

我们首先研究是否以及何时应用（不同的）数据增强是否有助于一般的图形对比学习。我们在图中总结了结果。2与从头开始训练相比（没有训练前）。我们列出了以下观察结果。

观察1。数据增强在图对比学习中至关重要。从图2中右上角的精度损失来看，没有任何数据增强图的对比学习没有帮助，通常比从头训练更差。 相比之下，创建一个原始图及其适当的增强可以有利于下游的性能。从图2中最上面的行或最右边的列来判断。在没有详尽的超参数调优的情况下，使用单次最佳增强的图对比学习取得了相当大的改进：NCI1为1.62%， PROTEINS为3.15%， COLLAB为6.27%，RDT-B为1.66%。

这个观察结果符合我们的直觉。在不增强的情况下，graphCL简单地将两个原始样本作为负对（正对损失为零），导致将所有图表示相互推开，这是无法证明的。重要的是，当应用适当的增强时，注入数据分布上的相应先验，使模型通过最大限度地提高图与其增强之间的一致性来强制模型学习对所需扰动不变的表示。

观察2。组合不同的增强功能的好处更多。组成一个图的增强对而不是图及其增强进一步提高了性能：NCI1的最大准确率增益为2.10%， PROTEINS为3.15%，COLLAB为7.11%，RDT-B为1.85%。有趣的是，应用相同类型的增强对(见图2中的对角线)与不同类型的增强对（非对角线）相比，通常不会导致最好的性能（节点下降除外）。在视觉表征学习[18]中也进行了类似的观察。正如在[18]中所推测的那样，组合不同的增强量避免了学习到的特征简单地过拟合低级的“捷径”，使特征更可一般化。

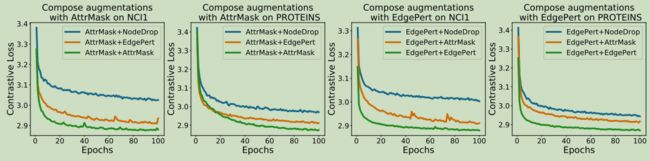
图3：不同增强对的对比损失曲线。在左边属性的两个图中，掩蔽与其他增强形成对比，右边的边缘扰动，其中对比相同的增强总是导致最快的损失下降。

在这里，我们做了一个类似的猜想，即对比不同类型的等构图对对图表示学习具有更困难但更有用的任务。因此，我们绘制了组成NCI1和PROTEINS的各种增强量（除子图外）的对比损失曲线，以及属性掩蔽或边缘扰动。图3中表明，当优化过程保持不变时，对于不同类型的增强对，对比损失总是比对于相同类型的增强对下降得更慢。这一结果表明，组合不同类型的增强对确实对应于一个“更难”的对比预测任务。我们将在Sec4.3中进行探讨如何在某些情况下量化一个“更难”的任务，以及它是否总是有帮助。

4.2，有效图形增强的类型、范围和模式

然后，我们注意到，增强类型的（最）有益的组合可以是特定于数据集的，这与我们的直觉相符，因为图结构的数据具有高度异构的性质(见Sec.1)。我们总结我们的观察并得出见解。我们进一步分析了给定类型的图增强的范围和/或模式的影响。

观察3。边缘扰动有利于社会网络，但会损害一些生化分子。边缘扰动作为成对的增强之一，提高了社交网络数据COLLAB、ROT-B以及生物分子数据PROTEINS的性能，但损害了其他生物分子数据NCI1。我们假设，与社交网络相比，一些生物分子数据的“语义项”对单个边缘更为敏感。具体来说，NCI1的单边变化对应于共价键的去除或添加，这可以极大地改变化合物的身份甚至有效性，更不用说它对下游语义的性质了。相比之下，社交网络的语义对个体边缘扰动[60,61]。因此，对于化合物，边缘扰动证明了一个在概念上与领域知识不相容的先验，并且在经验上对下游性能没有帮助。

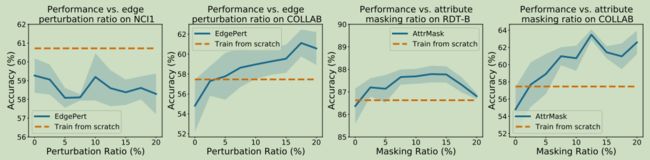
我们进一步研究了边缘扰动的程度或强度是否会影响上述结论。我们在有代表性的例子NCI1和COLLAB上评估了下游的性能。在我们的GraphCL框架中，我们使用了原始图（“相同的”）和不同比率的边缘扰动的组合。图4A表明，无论增强强度如何，边缘扰动都会恶化NCI1的性能，这证实了我们之前的结论对边缘扰动的程度不敏感。图B表明，随着增强强度的增加，边缘扰动可以进一步提高COLLAB性能。

观察4。应用属性掩蔽在更密集的图中取得了更好的性能。对于社交网络数据集，组合相同的图和属性掩蔽（平均度）提高5.12%，而RDT-B仅为0.17%。与NCI1相比，对更密集的PROTEINS也进行了类似的观察。为了评估增强强度对这一观察结果的影响，我们在RDT-B和COLLAB上进行了类似的实验，通过组成对比损失对比损失对比损失对比损失相同的图及其在不同程度上掩盖的属性。图4C和D表明，对非常稀疏的RDT-B掩蔽更少并没有帮助，尽管对非常密集的COLLAB掩蔽更多。

图4：性能与增强强度之间的关系。左两张图实现了不同比例的边缘扰动。右边的两个图应用了具有不同掩蔽比的属性掩蔽。

我们进一步假设掩蔽模式也很重要，根据消息传递机制[62]掩蔽更多的枢纽节点有利于更密集的图，因为gnn不能重建孤立节点缺失的信息。为了验证这一假设，我们进行了一个实验，在更密集的图PROTEINS和COLLAB上以更高的概率屏蔽具有更多连接的节点。具体来说，我们采用屏蔽分布   而不是均匀分布，其中degn是顶点vn的度，α是控制因子。α阳性表示高度节点的掩蔽更多。图5C和D表明，对于非常密集的COLLAB，如果屏蔽具有更多连接的节点，性能有明显的上升趋势。

观察5。节点下降和子图通常在不同的数据集之间是有益的。节点下降和子图，特别是后者，似乎在我们研究的数据集中是有益的。对于节点下降，强调缺少某些顶点（例如化合物中的一些氢原子或社交网络的边缘用户）不会改变语义信息的先验，这直观上符合我们的认知。对于子图，之前的工作[20,21]表明，强制执行局部（我们提取的子图）和全局信息一致性有助于表示学习，这解释了观察结果。即使对于NCI1中的化合物，子图也可以表示对下游语义很重要的结构和功能“基序”。

同样，我们通过采用在改变属性屏蔽模式中提到的非均匀分布来检查节点丢弃模式的影响。图5B表明，对于密集的社交网络COLLAB图，观察到更多的GraphCL改进，而枢纽节点在更多的范围内。图5A表明，对于不那么密集的PROTEINS图，改变节点下降分布从均匀性改变并不一定有帮助。

图5：性能与增强模式。节点下降和属性屏蔽采用各种控制因素（负到正：下降/屏蔽更多低度顶点到高级顶点）。

4.3，与“更硬”的任务不同，过于简单的对比任务并没有帮助。

正如在观察2中所讨论的，“更难”的对比学习可能受益更多，其中“更难”的任务是通过组合不同类型的增强量来实现的。在本节中，我们将进一步探讨与参数化增强强度/模式相关的可量化困难，并评估难度对性能改进的影响。

直观地看，更大的下降/掩蔽比或控制因子α导致了更困难的对比任务，这确实导致了在所考虑的范围内更好的COLLAB性能(图4和5）。非常小的比例或负的α，对应于过于简单的任务，我们还设计了增加难度水平的子图变量，并得出类似的结论。更多详细信息见附录D。

总结。总的来说，我们决定第5节的增强池为：生化分子的节点下降和子图；所有为密集的社交网络；除了稀疏社交网络的属性屏蔽。优势或模式是默认的，即使改变它们可能会有更多帮助。

5，与最先进的方法的比较

在本节中，我们比较了我们提出的（自监督）预训练框架GraphCL与最先进的方法(SOTAs)在半监督、无监督[21]和迁移学习[9]的图分类设置中(节点分类实验请参阅附录G)。具体设置的数据集统计数据和培训详细信息见附录E。

半监督学习。我们首先在基准的TU数据集[64]上的图分类[63,3]的半监督学习设置中评估我们提出的框架。由于图级任务的半监督学习中的预训练和微调在以前没有被探索过，我们采用两种传统的网络嵌入方法作为训练前任务进行比较：邻接信息重建(我们参考GAE[22]实现)和局部和全局表示一致性执行(参考Infomax[21]实现)。此外，还记录了从零开始训练和增强（没有对比）的表现。我们采用[63]中默认设置的图卷积网络(GCN)作为基于gnn的编码器，在全监督设置下实现了和SOTA相当的性能。表3显示，GraphCL的性能优于传统的预训练方案。

表3：带预训练和微调的半监督学习。红色数字表示最佳性能和与最佳性能（可比性能）的标准差重叠的数字。1%或10%为标签率；baseline和Aug.分别表示从头开始的训练。

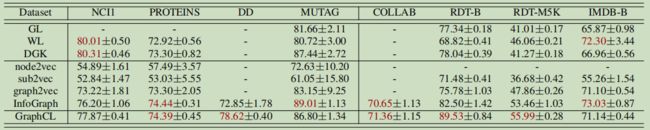
无监督的表示学习。此外，在[65,21]之后的无监督表示学习中对GraphCL进行评估，其中无监督方法生成图嵌入，这些嵌入被输入下游SVM分类器[21]。除了SOTA图核方法(GL)、维斯费勒-雷曼子树核(WL)和DGK核（深度图），我们还与四种无监督图级表示学习方法进行了比较，如node2vec[66]、sub2vec[67]、graph2vec[65]和InfoGraph[21]。我们采用[21]中默认设置的图同构网络(GIN)作为基于GNN的编码器，它在表示学习中是SOTA。表4显示了GraphCL在大多数情况下的表现更好，除了图大小小的数据集(例如MUTAG和IMDB-B由平均节点数小于20的图组成)。

迁移学习。最后，对[9]化学分子性质预测和蛋白质功能预测进行转移学习实验，对模型在不同数据集中进行预训练和细化，以评估预训练方案的可转移性。我们采用[9]中默认设置的GIN作为基于GNN的编码器，它在迁移学习中是SOTA。实验进行了10次，ROC-AUC评分的平均值和标准差（%）报告为[9]。虽然没有普遍有益的预训练方案，特别是对于迁移学习中的分布外场景(Sec.1)，表5显示，与之前的最佳方案相比，GraphCL在9个数据集中的5个上仍然达到了SOTA的性能。

表5：迁移学习与不同手工设计的预训练方案的比较，其中比较数字来自[9]。

对抗性鲁棒性。除了通用化之外，我们声称gnn也使用GraphCL获得了鲁棒性。实验在合成数据上进行，对图中的组件数进行分类，面对[60]中默认设置后的 RandSampling、GradArgmax和RL-S2V的攻击。 Structure2vec[68]在[60]中被采用为基于gnn的编码器。表6显示，在三次逃避攻击下，与从头开始的训练相比，GraphCL提高了GNN的鲁棒性。

表6：不同深度的GNN在三次对抗性攻击下的对抗性性能（遵循[60]中的协议）。红色的数字表示性能最好。

6，结论

在本文中，我们进行了显式的研究来探索GNN预训练的对比学习，面对图结构数据的独特挑战。首先，提出了几种图数据的增强，并讨论了引入某些人的数据分布先验。随着新的增强，我们提出了一种新的图对比学习框架(GraphCL)用于GNN预训练，以促进学习不变的表示和严格的理论分析。我们系统地评估和分析了我们提出的框架中数据增强的影响，揭示了增强的基本原理和指导增强的选择。实验结果验证了我们提出的框架在通用性和鲁棒性方面的最先进的性能。

更广泛的影响

授权深度学习在图结构数据上进行推理和预测具有广泛的兴趣和广泛的应用，如推荐系统、神经体系结构搜索和药物发现。所提出的与增强的图对比学习框架提供了一个通用的框架，可以通过模型预训练潜在地有利于图神经网络的有效性和效率。数值结果和分析也将启发设计适当的增强，以积极的知识转移的下游任务。

References

[1] Thomas N Kipf and Max Welling. Semi-supervised classifification with graph convolutional networks.

arXiv preprint arXiv:1609.02907, 2016.

[2] Petar Velickovic, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio.

Graph attention networks. arXiv preprint arXiv:1710.10903, 2017.

[3] Keyulu Xu, Weihua Hu, Jure Leskovec, and Stefanie Jegelka. How powerful are graph neural networks?

arXiv preprint arXiv:1810.00826, 2018.

[4] Yuning You, Tianlong Chen, Zhangyang Wang, and Yang Shen. L2 -gcn: Layer-wise and learned effificient

training of graph convolutional networks. In Proceedings of the IEEE/CVF Conference on Computer

Vision and Pattern Recognition, pages 2127–2135, 2020.

[5] Meng Liu, Hongyang Gao, and Shuiwang Ji. Towards deeper graph neural networks. In Proceedings of the

26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pages 338–348,

2020.

[6] Difan Zou, Ziniu Hu, Yewen Wang, Song Jiang, Yizhou Sun, and Quanquan Gu. Layer-dependent

importance sampling for training deep and large graph convolutional networks. In Advances in Neural

Information Processing Systems, pages 11249–11259, 2019.

[7] Muhan Zhang and Yixin Chen. Link prediction based on graph neural networks. In Advances in Neural

Information Processing Systems, pages 5165–5175, 2018.

[8] Zhitao Ying, Jiaxuan You, Christopher Morris, Xiang Ren, Will Hamilton, and Jure Leskovec. Hierarchical

graph representation learning with differentiable pooling. In Advances in Neural Information Processing

Systems, pages 4800–4810, 2018.

[9] Weihua Hu, Bowen Liu, Joseph Gomes, Marinka Zitnik, Percy Liang, Vijay Pande, and Jure Leskovec.

Pre-training graph neural networks. arXiv preprint arXiv:1905.12265, 2019.

[10] Dumitru Erhan, Pierre-Antoine Manzagol, Yoshua Bengio, Samy Bengio, and Pascal Vincent. The diffificulty

of training deep architectures and the effect of unsupervised pre-training. In Artifificial Intelligence and

Statistics, pages 153–160, 2009.

[11] Xavier Glorot and Yoshua Bengio. Understanding the diffificulty of training deep feedforward neural

networks. In Proceedings of the thirteenth international conference on artifificial intelligence and statistics,

pages 249–256, 2010.

[12] Vijay Prakash Dwivedi, Chaitanya K Joshi, Thomas Laurent, Yoshua Bengio, and Xavier Bresson. Bench

marking graph neural networks. arXiv preprint arXiv:2003.00982, 2020.

[13] Qimai Li, Zhichao Han, and Xiao-Ming Wu. Deeper insights into graph convolutional networks for

semi-supervised learning. In Thirty-Second AAAI Conference on Artifificial Intelligence, 2018.

[14] Kenta Oono and Taiji Suzuki. Graph neural networks exponentially lose expressive power for node

classifification. arXiv preprint cs.LG/1905.10947, 2019.

[15] Marinka Zitnik, Jure Leskovec, et al. Prioritizing network communities. Nature communications, 9(1):1–9,

2018.

[16] Priya Goyal, Dhruv Mahajan, Abhinav Gupta, and Ishan Misra. Scaling and benchmarking self-supervised

visual representation learning. arXiv preprint arXiv:1905.01235, 2019.

[17] Alexander Kolesnikov, Xiaohua Zhai, and Lucas Beyer. Revisiting self-supervised visual representation

learning. arXiv preprint arXiv:1901.09005, 2019.

[18] Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. A simple framework for

contrastive learning of visual representations. arXiv preprint arXiv:2002.05709, 2020.

[19] Weihua Hu, Matthias Fey, Marinka Zitnik, Yuxiao Dong, Hongyu Ren, Bowen Liu, Michele Catasta,

and Jure Leskovec. Open graph benchmark: Datasets for machine learning on graphs. arXiv preprint

arXiv:2005.00687, 2020.

[20] Petar Veli

ˇ

ckovi

´

c, William Fedus, William L Hamilton, Pietro Liò, Yoshua Bengio, and R Devon Hjelm.

Deep graph infomax. arXiv preprint arXiv:1809.10341, 2018.

[21] Fan-Yun Sun, Jordan Hoffmann, and Jian Tang. Infograph: Unsupervised and semi-supervised graph-level

representation learning via mutual information maximization. arXiv preprint arXiv:1908.01000, 2019.

[22] Thomas N Kipf and Max Welling. Variational graph auto-encoders. arXiv preprint arXiv:1611.07308,

2016.

[23] Will Hamilton, Zhitao Ying, and Jure Leskovec. Inductive representation learning on large graphs. In

Advances in neural information processing systems, pages 1024–1034, 2017.

[24] Leonardo FR Ribeiro, Pedro HP Saverese, and Daniel R Figueiredo. struc2vec: Learning node represen

tations from structural identity. In Proceedings of the 23rd ACM SIGKDD International Conference on

Knowledge Discovery and Data Mining, pages 385–394, 2017.

[25] Zhirong Wu, Yuanjun Xiong, Stella X Yu, and Dahua Lin. Unsupervised feature learning via non

parametric instance discrimination. In Proceedings of the IEEE Conference on Computer Vision and

Pattern Recognition, pages 3733–3742, 2018.

[26] Mang Ye, Xu Zhang, Pong C Yuen, and Shih-Fu Chang. Unsupervised embedding learning via invariant

and spreading instance feature. In Proceedings of the IEEE Conference on Computer Vision and Pattern

Recognition, pages 6210–6219, 2019.

[27] Xu Ji, João F Henriques, and Andrea Vedaldi. Invariant information clustering for unsupervised image

classifification and segmentation. In Proceedings of the IEEE International Conference on Computer Vision,

pages 9865–9874, 2019.

[28] Kaiming He, Haoqi Fan, Yuxin Wu, Saining Xie, and Ross Girshick. Momentum contrast for unsupervised

visual representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and

Pattern Recognition, pages 9729–9738, 2020.

[29] Mehdi Noroozi and Paolo Favaro. Unsupervised learning of visual representations by solving jigsaw

puzzles. In European Conference on Computer Vision, pages 69–84. Springer, 2016.

[30] Fabio M Carlucci, Antonio D’Innocente, Silvia Bucci, Barbara Caputo, and Tatiana Tommasi. Domain

generalization by solving jigsaw puzzles. In Proceedings of the IEEE Conference on Computer Vision

and Pattern Recognition, pages 2229–2238, 2019.

[31] Trieu H Trinh, Minh-Thang Luong, and Quoc V Le. Selfifie: Self-supervised pretraining for image

embedding. arXiv preprint arXiv:1906.02940, 2019.

[32] Tianlong Chen, Sijia Liu, Shiyu Chang, Yu Cheng, Lisa Amini, and Zhangyang Wang. Adversarial

robustness: From self-supervised pre-training to fifine-tuning. arXiv preprint arXiv:2003.12862, 2020.

[33] Roei Herzig, Amir Bar, Huijuan Xu, Gal Chechik, Trevor Darrell, and Amir Globerson. Learning canonical

representations for scene graph to image generation. arXiv preprint arXiv:1912.07414, 2019.

[34] Yuning You, Tianlong Chen, Zhangyang Wang, and Yang Shen. When does self-supervision help graph

convolutional networks? arXiv preprint arXiv:2006.09136, 2020.

[35] Wei Jin, Tyler Derr, Haochen Liu, Yiqi Wang, Suhang Wang, Zitao Liu, and Jiliang Tang. Self-supervised

learning on graphs: Deep insights and new direction. arXiv preprint arXiv:2006.10141, 2020.

[36] Qikui Zhu, Bo Du, and Pingkun Yan. Self-supervised training of graph convolutional networks. arXiv

preprint arXiv:2006.02380, 2020.

[37] Jiawei Zhang, Haopeng Zhang, Li Sun, and Congying Xia. Graph-bert: Only attention is needed for

learning graph representations. arXiv preprint arXiv:2001.05140, 2020.

[38] Ziniu Hu, Yuxiao Dong, Kuansan Wang, Kai-Wei Chang, and Yizhou Sun. Gpt-gnn: Generative pre

training of graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference

on Knowledge Discovery & Data Mining, pages 1857–1867, 2020.

[39] Xiao Liu, Fanjin Zhang, Zhenyu Hou, Zhaoyu Wang, Li Mian, Jing Zhang, and Jie Tang. Self-supervised

learning: Generative or contrastive. arXiv preprint arXiv:2006.08218, 2020.

[40] Vikas Verma, Meng Qu, Alex Lamb, Yoshua Bengio, Juho Kannala, and Jian Tang. Graphmix: Regularized

training of graph neural networks for semi-supervised learning. arXiv preprint arXiv:1909.11715, 2019.

[41] Ming Ding, Jie Tang, and Jie Zhang. Semi-supervised learning on graphs with generative adversarial nets.

In Proceedings of the 27th ACM International Conference on Information and Knowledge Management,

pages 913–922, 2018.

[42] Zhijie Deng, Yinpeng Dong, and Jun Zhu. Batch virtual adversarial training for graph convolutional

networks. arXiv preprint arXiv:1902.09192, 2019.

[43] Fuli Feng, Xiangnan He, Jie Tang, and Tat-Seng Chua. Graph adversarial training: Dynamically regulariz

ing based on graph structure. IEEE Transactions on Knowledge and Data Engineering, 2019.

[44] Michael T Rosenstein, Zvika Marx, Leslie Pack Kaelbling, and Thomas G Dietterich. To transfer or not to

transfer. In NIPS 2005 workshop on transfer learning, volume 898, pages 1–4, 2005.

[45] Suzanna Becker and Geoffrey E Hinton. Self-organizing neural network that discovers surfaces in random

dot stereograms. Nature, 355(6356):161–163, 1992.

[46] Mohamed Ishmael Belghazi, Aristide Baratin, Sai Rajeswar, Sherjil Ozair, Yoshua Bengio, Aaron Courville,

and R Devon Hjelm. Mine: mutual information neural estimation. arXiv preprint arXiv:1801.04062, 2018.

[47] R Devon Hjelm, Alex Fedorov, Samuel Lavoie-Marchildon, Karan Grewal, Phil Bachman, Adam Trischler,

and Yoshua Bengio. Learning deep representations by mutual information estimation and maximization.

arXiv preprint arXiv:1808.06670, 2018.

[48] Zhen Peng, Yixiang Dong, Minnan Luo, Xiao-Ming Wu, and Qinghua Zheng. Self-supervised graph

representation learning via global context prediction. arXiv preprint arXiv:2003.01604, 2020.

[49] Qizhe Xie, Zihang Dai, Eduard Hovy, Minh-Thang Luong, and Quoc V Le. Unsupervised data augmenta

tion. arXiv preprint arXiv:1904.12848, 2019.

[50] David Berthelot, Nicholas Carlini, Ian Goodfellow, Nicolas Papernot, Avital Oliver, and Colin A Raffel.

Mixmatch: A holistic approach to semi-supervised learning. In Advances in Neural Information Processing

Systems, pages 5050–5060, 2019.

[51] Kihyuk Sohn. Improved deep metric learning with multi-class n-pair loss objective. In Advances in neural

information processing systems, pages 1857–1865, 2016.

[52] Aaron van den Oord, Yazhe Li, and Oriol Vinyals. Representation learning with contrastive predictive

coding. arXiv preprint arXiv:1807.03748, 2018.

[53] Ting Chen, Yizhou Sun, Yue Shi, and Liangjie Hong. On sampling strategies for neural network-based

collaborative fifiltering. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge

Discovery and Data Mining, pages 767–776, 2017.

[54] Petar Velickovic, William Fedus, William L Hamilton, Pietro Liò, Yoshua Bengio, and R Devon Hjelm.

Deep graph infomax. In ICLR (Poster), 2019.

[55] Yuxiang Ren, Bo Liu, Chao Huang, Peng Dai, Liefeng Bo, and Jiawei Zhang. Heterogeneous deep graph

infomax. arXiv preprint arXiv:1911.08538, 2019.

[56] Chanyoung Park, Donghyun Kim, Jiawei Han, and Hwanjo Yu. Unsupervised attributed multiplex network

embedding. In AAAI, pages 5371–5378, 2020.

[57] Zhen Peng, Wenbing Huang, Minnan Luo, Qinghua Zheng, Yu Rong, Tingyang Xu, and Junzhou Huang.

Graph representation learning via graphical mutual information maximization. In Proceedings of The Web

Conference 2020, pages 259–270, 2020.

[58] Kaveh Hassani and Amir Hosein Khasahmadi. Contrastive multi-view representation learning on graphs.

arXiv preprint arXiv:2006.05582, 2020.

[59] Jiezhong Qiu, Qibin Chen, Yuxiao Dong, Jing Zhang, Hongxia Yang, Ming Ding, Kuansan Wang, and Jie

Tang. Gcc: Graph contrastive coding for graph neural network pre-training. In Proceedings of the 26th

ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pages 1150–1160,

2020.

[60] Hanjun Dai, Hui Li, Tian Tian, Xin Huang, Lin Wang, Jun Zhu, and Le Song. Adversarial attack on graph

structured data. arXiv preprint arXiv:1806.02371, 2018.

[61] Daniel Zügner, Amir Akbarnejad, and Stephan Günnemann. Adversarial attacks on neural networks for

graph data. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery

& Data Mining, pages 2847–2856, 2018.

[62] Justin Gilmer, Samuel S Schoenholz, Patrick F Riley, Oriol Vinyals, and George E Dahl. Neural mes

sage passing for quantum chemistry. In Proceedings of the 34th International Conference on Machine

Learning-Volume 70, pages 1263–1272. JMLR. org, 2017.

[63] Ting Chen, Song Bian, and Yizhou Sun. Are powerful graph neural nets necessary? a dissection on graph

classifification. arXiv preprint arXiv:1905.04579, 2019.

[64] Christopher Morris, Nils M. Kriege, Franka Bause, Kristian Kersting, Petra Mutzel, and Marion Neumann.

Tudataset: A collection of benchmark datasets for learning with graphs. In ICML 2020 Workshop on

Graph Representation Learning and Beyond (GRL+ 2020), 2020.

[65] Annamalai Narayanan, Mahinthan Chandramohan, Rajasekar Venkatesan, Lihui Chen, Yang Liu, and Shan

tanu Jaiswal. graph2vec: Learning distributed representations of graphs. arXiv preprint arXiv:1707.05005,

2017.

[66] Aditya Grover and Jure Leskovec. node2vec: Scalable feature learning for networks. In Proceedings of the

22nd ACM SIGKDD international conference on Knowledge discovery and data mining, pages 855–864,

2016.

[67] Bijaya Adhikari, Yao Zhang, Naren Ramakrishnan, and B Aditya Prakash. Sub2vec: Feature learning

for subgraphs. In Pacifific-Asia Conference on Knowledge Discovery and Data Mining, pages 170–182.

Springer, 2018.

[68] Hanjun Dai, Bo Dai, and Le Song. Discriminative embeddings of latent variable models for structured

data. In International conference on machine learning, pages 2702–2711, 2016.