Hybrid A *算法原理及实现步骤
目录
1.Hybrid A *算法原理
2.Hybrid A*规划路径的组成
3.Hybrid A*的启发式
4、实现步骤
1.Hybrid A *算法原理
Hybrid A*是连续坐标系下进行启发式搜索,并且能够保证生成的轨迹满足车辆非完整性约束(运动学约束),但算法运行过程中该路径并不一定是全局最优。(在全局最优解的”附近”)。
(Hybrid A*算法是一种图搜索算法,改进于A*算法。与普通的A*算法区别在于,Hybrid A*规划的路径考虑了车辆的运动学约束,即满足了车辆的最大曲率约束。)
Hybrid A*是基于网格地图,A*赋予每个网格的中心点相应的损失并且算法是访问这些中心点;而hybrid A*是在网格中挑选满足车辆3d连续状态点,并将损失值赋值给该点。
2.Hybrid A*规划路径的组成
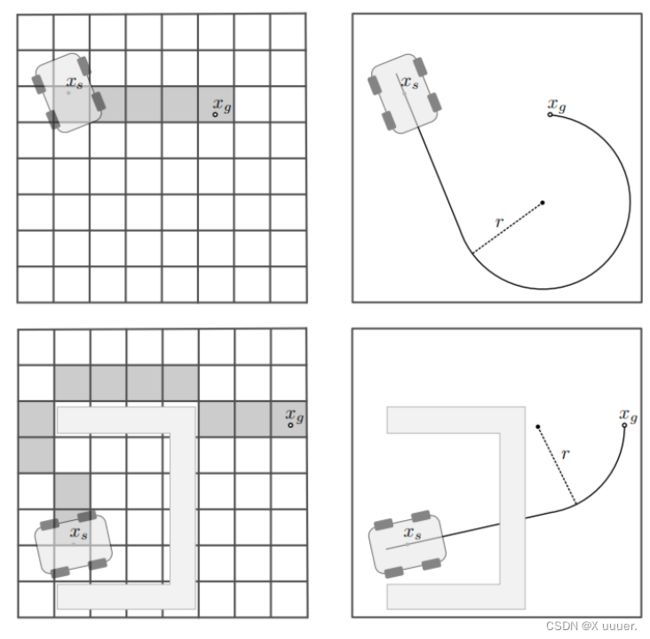
Hybrid A*规划的路径由两部分组成,第一部分是考虑了车辆运动学的探索结点连接而成的路径;第二部分是使用ReedSheeps曲线连接中间点位姿与目标位姿的路径。
1)Hybrid A*的结点拓展
Hybrid A*的搜索空间不仅考虑了x,y方向的拓展,还考虑了Θ方向的探索。相比普通A*的探索空间,Hybrid A*的结点拓展是三维的,因此需要更多的计算量。
2)Analytical Expansion
Hyrbrid A*偶尔会尝试使用RS曲线或Dubins曲线尝试连接当前的结点与目标结点。这一方面可以精确地连接到目标位姿,另一方向可提高搜索的速度。如果得到的曲线与环境障碍物无碰撞,可以提取结束搜索。(Reeds-Shepp曲线由几段半径固定的圆弧和一段直线段拼接组成,而且圆弧的半径就是汽车的最小转向半径。这里的路径长度是指汽车中心运动轨迹的长度,也就是所有圆弧的弧长和直线段的长度之和。)
这一操作在接近目标位姿或者非常稀疏的环境中比较有作用。如果每次尝试连接都需要做碰撞检测,会极大增加计算量。
3.Hybrid A*的启发式
Hybrid A*的有两个启发式: non-holonomic without-obstacles和holonomic with obstacles。
一般会取二者的最大值作为约束。
1、其中约束启发式无视周围障碍物但考虑的车辆本身的特性。这种启发式约束考虑了当前位置、航向角以及转弯半径,可以确保车辆以正确的航向接近目标位姿。当车辆越来越接近目标时,这一约束会发挥较重要的作用。为了计算,将终点的状态(xg, yg, θg)设为(0,0,0), 并在完全没有障碍物的情况下,计算从目标的某个离散邻域中的每个点(x,y,θ)到目标的最短路径。然后,我们使用non-holonomic-without-obstacles 代价的最大值和二维欧几里的距离作为我们的启发式。这种启发式方法的效果是,它修剪了一些搜索分支。
2、 无约束启发式则忽略了汽车的非完整性,但是利用障碍图在二维空间进行动态规划,计算到目标的最短距离,这个考虑了障碍物的启发式可以引导车辆绕过障碍物或U型弯道。
(传统的A*算法计算每个节点到终点的最短路径)。
4、实现步骤
1、额外加的规划条件约束:规划时间、目的性
2、进行采样,离散的获得一些轨迹点以及起始点的速度与加速度,得到节点point_set,即创建open_list
3、将起始点及目标点的三维位置转化至栅格地图的index. 并计算第一个扩展点的Heuristic cost
4、迭代循环搜索扩张节点,扩张节点的同时不断进行两点边界的直达曲线计算
1)从open_list优先级队列中取出f(n) = g(n) + h(n)代价值最小的节点
2)判断当前节点是否超出horizon或是离终点较近了,并计算一条直达曲线,检查这条曲线上是否存在。若存在,则搜索完成,返回路径点即可
3)若当前节点没有抵达终点,就要进行节点扩张-剪枝:
1、在open_list中删除节点,并在close_list中添加节点
2、初始化状态传递
3、判断节点是已经被扩展过
4、状态传递循环迭代,检查速度约束,检查碰撞,都通过的话,就计算当前节点的g_score以及f_score,并且对重复的扩展节点进行剪枝:
判断节点若在不在close_list中
判断节点最大速度
判断节点不在同样的网格中
判断节点是否发生碰撞
状态传递,通过前向积分得到扩展节点的位置和速度stateTransit()
计算当前节点的真实的代价G值
计算启发式代价H值
在循环中对比扩展节点,进行节点剪枝
4)open_list已经遍历完成了,没有搜索到路径 open set empty, no path
5、获取规划得到的路径点