OpenCV实现击中击不中变换和形态学细化

1 击中击不中变换

1.1 HMT概述

形态学Hit-or-Miss是形状检测基本工具，只要结构元设置得当，就可以检测一些基本的形状图案，HMT变换只能作用于二值图像，结构元（核）元素值由0、1、-1组成。

操作时，结构元在图像上滑动，覆盖一小片与核大小一样的区域，然后逐一对比，核的值为1时，覆盖区域对应位置必须为255，而核值为-1时，则必须为0，核值为0时0和255均可，如果覆盖区域所有的位置均满足上述要求，则表示击中，锚点位置设置为255，如果有任意一个位置不满足，则表示击不中，锚点位置设置为0。

不过HMT单独用来作为通俗意义上的形状检测并不是很常用（个人理解），一般都是作为其他形态学算法的基础，例如：凸壳、细化、骨架化等。

1.2 代码实现

下面简单演示一下HMT的简单实现代码和固定尺寸矩形的检测

//func:			击中击不中变换：Hitmiss-----> 核中-1与图像中0对应，1与255对应，0任意对应
//matpadded:	输入已进行边界扩展的二值化图像
cv::Mat _hit_or_miss(const cv::Mat& matpadded, const cv::Mat& kernel)
{
	CV_Assert(matpadded.type() == CV_8UC1);
	CV_Assert(kernel.type() == CV_32SC1);			//含有负数，选int类型

	int rows = matpadded.rows - kernel.rows + 1;
	int cols = matpadded.cols - kernel.cols + 1;
	cv::Mat mat = cv::Mat::zeros(rows, cols, CV_8UC1);

	for (int i = 0; i < mat.rows; ++i)
	{
		for (int j = 0; j < mat.cols; ++j)
		{
			bool isGood = true;
			cv::Mat roi(matpadded, cv::Rect(j, i, kernel.cols, kernel.rows));
			//进行击中击不中判断
			for (int ii = 0; ii < kernel.rows; ++ii)
			{
				uchar* roi_p = roi.ptr<uchar>(ii);
				const int* kernel_p = kernel.ptr<int>(ii);

				for (int jj = 0; jj < kernel.cols; ++jj)
				{
					if ((kernel_p[jj] == 1 && roi_p[jj] == 0) || (kernel_p[jj] == -1 && roi_p[jj] == 255))
					{
						isGood = false;
						break;
					}
				}
				if (!isGood)
					break;
			}

			mat.ptr<uchar>(i)[j] = (isGood ? 255 : 0);
		}
	}

	return mat;
}


/*
在测试图像中创建若干个4X4填充矩形，和边长大于4的矩形，利用HMT对4x4矩形进行检测
结构元设置为{-1，-1，-1，-1，-1，-1
            -1,1,1,1,1，-1
            -1,1,1,1,1，-1
            -1,1,1,1,1，-1
            -1,1,1,1,1，-1
            -1，-1，-1,-1，-1，-1}；
即在矩形的外圈填充一圈-1，以此来确定矩形的边界。
*/

int main()
{
    cv::Mat kernel = (cv::Mat_<int>(6, 6) <<
		-1, -1, -1, -1, -1, -1,
		-1, 1, 1, 1, 1, -1,
		-1, 1, 1, 1, 1, -1,
		-1, 1, 1, 1, 1, -1,
		-1, 1, 1, 1, 1, -1,
		-1, -1, -1, -1, -1, -1);
	cv::Size shapeSize = kernel.size();
	cv::Mat matPadded;
	cv::Mat myHitmiss, opencvHitmiss;

	//边界拓展的原则是：如果锚点在核中心，当核的尺寸为偶数时，左和上边界要比其他两边界多1
	int left = shapeSize.width / 2;
	int right = shapeSize.width % 2 == 0 ? shapeSize.width / 2 - 1 : shapeSize.width / 2;
	int top = shapeSize.height / 2;
	int bottom = shapeSize.height % 2 == 0 ? shapeSize.height / 2 - 1 : shapeSize.height / 2;

	//创建测试图像
	cv::Mat test = cv::Mat::zeros(300, 300, CV_8UC1);
	cv::rectangle(test, cv::Rect(20, 20, 4, 4), cv::Scalar(255), cv::FILLED);
	cv::rectangle(test, cv::Rect(50, 20, 4, 4), cv::Scalar(255), cv::FILLED);
	cv::rectangle(test, cv::Rect(20, 60, 4, 4), cv::Scalar(255), cv::FILLED);
	cv::rectangle(test, cv::Rect(60, 20, 4, 4), cv::Scalar(255), cv::FILLED);
	cv::rectangle(test, cv::Rect(80, 40, 6, 6), cv::Scalar(255), cv::FILLED);
	cv::rectangle(test, cv::Rect(100, 80, 10, 8), cv::Scalar(255), cv::FILLED);

	cv::copyMakeBorder(test, matPadded, top, bottom, left, right, cv::BORDER_REFLECT101);

	myHitmiss = _hit_or_miss(matPadded, kernel);
	cv::morphologyEx(test, opencvHitmiss, cv::MORPH_HITMISS, kernel);

	cv::imshow("myhitmiss", myHitmiss);
	cv::imshow("opencvHitmiss", opencvHitmiss);

	cv::waitKey(0);
	return 0;
}

1.3 结果展示

在结果图中形成了一些小白点，即检测到的规定尺寸大小矩形的中心

---

2 形态学细化

2.1 概述

在众多博客中看到了各种各样的细化版本，本人学识较浅，实在是读不懂别人的代码，就花了一点时间理解了一下冈萨雷斯《数字图像处理》形态学细化篇章，并做了一个代码实现。

形态学细化由我的理解来说就是：利用前辈们总结的一组结构元，不断循环重复的进行HMT变换，直至结果收敛（不在变换），单次细化公式定义为：

其中$A$为源图像，$B$为结构元，编程时主要采用中间哪项定义即：用输出图 = 源图像 - 结构元对源图像进行HMT变换的结果。

其中$B$为：

依据这一结构元序列将细化定义为：

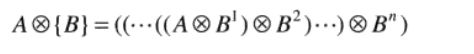
这一处理过程就是$A$被$B^1$细化一次，得到的结果然后被$B^2$细化一次，以此类推，一直套娃下去，直至得到的结果不在出现变化为止。

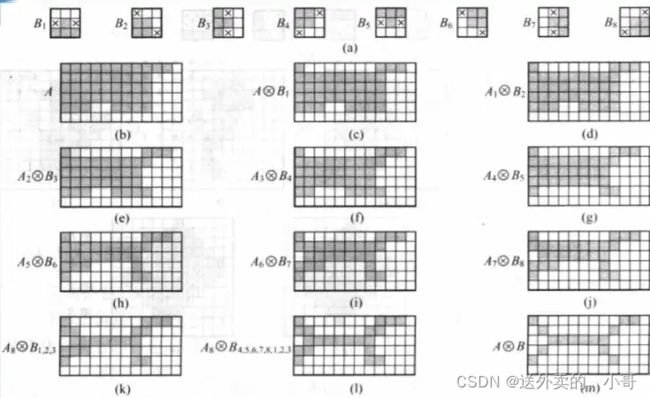
对于图片中的结构元，黑色代表前景值为1，白色为背景值为-1，x的值为0.

2.2 代码实现

只做简单实现，耗时在100ms左右。

//单次图像细化
//输入二值化图像
static void Morph_Thinning(const cv::Mat& src, const cv::Mat& kernel, cv::Mat& dst)
{
	CV_Assert(src.type() == CV_8UC1);
	CV_Assert(kernel.type() == CV_32SC1);

	cv::Mat tmpdst;
	cv::morphologyEx(src, tmpdst, cv::MORPH_HITMISS, kernel);
	dst = src - tmpdst;
}

/*
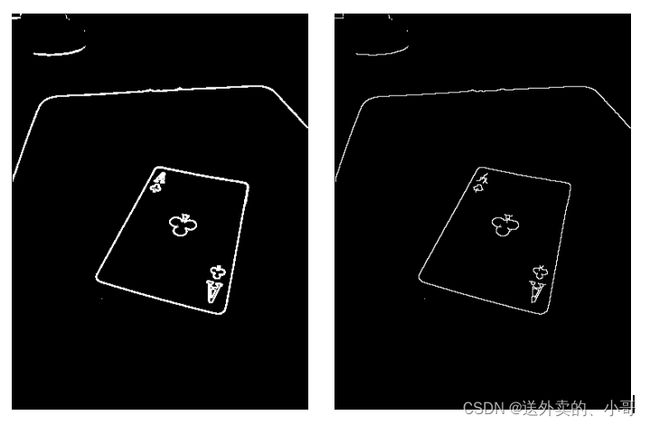
对一副图像计算梯度幅值图像，将二值化后的幅值图像进行细化
*/

int main()
{
	std::string path = "F:\\NoteImage\\扑克牌2.jpg";

	cv::Mat src = cv::imread(path, cv::IMREAD_GRAYSCALE);
	if (!src.data) {
		std::cout << "Could not open or find the image" << std::endl;
		return -1;
	}

	cv::Mat dx, dy;
	cv::Sobel(src, dx, CV_32FC1, 1, 0);
	cv::Sobel(src, dy, CV_32FC1, 0, 1);

	cv::Mat mag;
	cv::magnitude(dx, dy, mag);
	cv::normalize(mag, mag, 0, 255, cv::NORM_MINMAX);
	mag.convertTo(mag, CV_8UC1);

	cv::Mat thres;
	cv::threshold(mag, thres, 50, 255, cv::THRESH_BINARY);

	//创建结构元序列
	std::vector<std::vector<int>> Kernel_array = {
		{-1,-1,-1,0,1,0,1,1,1},
		{0,-1,-1,1,1,-1,1,1,0},
		{1,0,-1,1,1,-1,1,0,-1},
		{1,1,0,1,1,-1,0,-1,-1},
		{1,1,1,0,1,0,-1,-1,-1},
		{0,1,1,-1,1,1,-1,-1,0},
		{-1,0,1,-1,1,1,-1,0,1},
		{-1,-1,0,-1,1,1,0,1,1}
	};

	std::vector<cv::Mat> kernels(Kernel_array.size());
	for (int i = 0; i < Kernel_array.size(); ++i)
	{
		cv::Mat kernel = cv::Mat(Kernel_array[i]).reshape(0, 3);
		kernels[i] = kernel;
	}

	int iterations = 0;					//迭代次数
	int equalCount = 0;					//收敛次数
	const int Max_Iterations = 100;		//最大迭代次数

	cv::Mat dst = thres.clone();

	double t = cv::getTickCount();

	while (iterations < Max_Iterations)
	{
		cv::Mat tempdst = dst.clone();
		const int index = iterations % 8;

		Morph_Thinning(dst, kernels[index], dst);
        //判断这一次的结果和上一次是否相等
		cv::Mat diff = (tempdst != dst);
		bool equal = (cv::countNonZero(diff) == 0);

		if (equal)
			equalCount++;
		else
			equalCount = 0;

		//收敛次数超过两次退出
		if (equalCount > 2)
			break;

		iterations++;
	}
	//计算时间打印结果
	double timepass = (cv::getTickCount() - t) / cv::getTickFrequency();
	std::cout << iterations << std::endl;
	std::cout << timepass << std::endl;

	cv::imshow("Thinning_dst", dst);
	cv::waitKey(0);
	return 0;
}

2.3 实验结果

看的出来边缘被明显细化，但要达到真正的1像素宽边缘，还要将细化后元素转化为m连通，这一步骤下期再见！