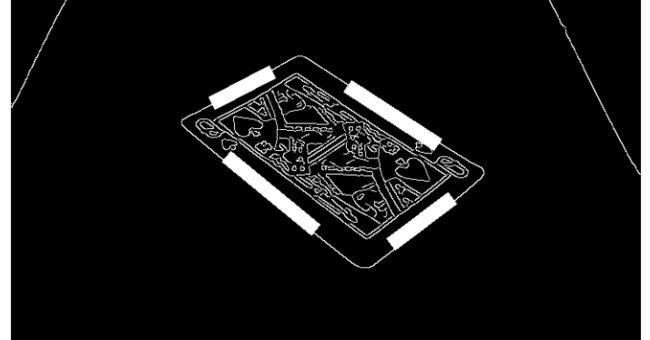
OpenCV综合练习2——扑克牌(文本)校正

图像处理综合练习2——多角度扑克牌校正

这是我刚开始学习图像处理时在B站上所接触的一个文本校正小练习，但是视频中的场景角度单一，只能校正固定视角下的文本，相对简单，但对于初学者来说的确是很好的入门材料。特此，针对视频中，文本校正这个练习，我增加了一点点难度，将文本换成扑克牌（正确对待扑克牌圆角），并在多视角下均可校正。

完整的项目资源：多视角扑克牌(文本)校正

---

项目需求

源自b站上的一个小练习，这里将文本换做扑克牌，在这个项目中需要处理的难点是：

• 扑克牌顶点处为圆角，使用OpenCV多边形拟合四边形得到的顶点不能代表其真实的顶点，需要通过扑克牌边缘直线求交点从而获得真实顶点。
• 要求得扑克牌边缘直线用霍夫直线变换鲁棒性不强，所以需要找到扑克牌边缘像素点通过最小二乘法来拟合直线从而求交点。
• 在任意视角下均可进行校正，处理的扑克牌数量原则上不限。
• 透视变换需要将变换前的点和变换后的点一一对应，但通过求直线交点获得的顶点顺序是杂乱的，所以需要通过扑克牌倾斜方向调整扑克牌顶点顺序以便正确的进行透视变换。

整体来说偏简单，算法重在逻辑关系，有兴趣的小伙伴可以尝试一下。

一、图像预处理

1. Canny边缘求取

将源图像进行灰度化并进行高斯滤波，图像中扑克牌背景我采用的黑色，直接使用canny边缘提取算法，完成边缘提取，低阈值为75，高阈值为低阈值的2倍。

  //灰度化，并高斯滤波
	cv::Mat src_gray, src_Canny;
	cv::cvtColor(src, src_gray, cv::COLOR_BGR2GRAY);
	cv::GaussianBlur(src_gray, src_gray, cv::Size(7, 7), 0, 0);

	//canny边缘提取
	double threshold = 75;
	cv::Canny(src_gray, src_Canny, threshold, threshold * 2, 3);

2. 轮廓提取并进行多边形拟合

将边缘图像进行轮廓提取，并将满足面积阈值的轮廓进行多边形拟合，当拟合结果为四边形，保存并返回该拟合结果以便后续算法处理。

/** @brief 对边缘图像提取外轮廓，并进行多边形拟合，并将拟合结果为四边形的多边形返回

@param Cannymat: 传入的边缘图像，CV_8UC1
@param thresh_area: 轮廓所围面积阈值，用于排除小轮廓
*/
std::vector<std::vector<cv::Point>> find_quadrilateral(cv::Mat& Cannymat, const int thresh_area)
{
	CV_Assert(Cannymat.type() == CV_8UC1);

	std::vector<std::vector<cv::Point>> contours;
	std::vector<std::vector<cv::Point>> quad_contours;
	cv::findContours(Cannymat, contours, cv::RETR_EXTERNAL, cv::CHAIN_APPROX_NONE, cv::Point());

	for (int i = 0; i < contours.size(); ++i)
	{
		if (cv::contourArea(contours[i], false) > thresh_area)		//满足面积条件
		{
			std::vector<cv::Point> approxCurve;

			double length = cv::arcLength(contours[i], true);
			cv::approxPolyDP(contours[i], approxCurve, 0.02 * length, true);

			if (approxCurve.size() == 4)
				quad_contours.push_back(approxCurve);
		}
	}

	return quad_contours;
}

将拟合的多边形进行可视化：

拟合的四边形可以在很大程度上代表扑克牌，但拟合的顶点与扑克牌真正的顶点还是相差甚远，要想定位到更精确的顶点还需要进一步处理。

二、四边形拟合顶点顺序重排

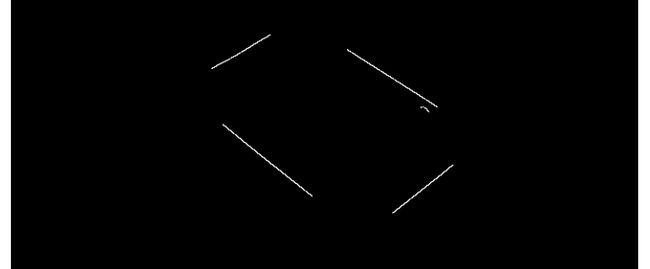
通过测试OpenCV多边形拟合函数cv::approxPolyDP()拟合得到的顶点是顺序排列的，不会出现两点连线是对角线的情况，顺序重排就是为了避免出现两点是对角线的情况，但是为了保险起见，我还是做了拟合顶点的顺序重排，所以这一步在这里是可有可无的。

重排的顺序如上图所示，重排的规则是为了对应透视变换后将扑克牌变换为竖直状态（后续代码会继续用到重排顶点顺序的算法）。

1. 顶点重排算法

选取一个点作为基点，计算其他三个点到基点的距离，距离最短的点为第二个点，距离最长的点为第四个点，自然剩下的那个点为第三个点。这种排序方式满足大多数情况，某种极端情况下会出现对角线长度略小于扑克牌的长边，所以，当最长边与对角线长度差值小于一个阈值时，计算1-3,1-4与1-2向量的点积，点积越大的证明所形成的角度越小，就可以确定对角线点了，具体的代码如下：

//二维向量点积计算
static float dot_product(cv::Point base, cv::Point pt1, cv::Point pt2)
{
	cv::Point vec1(pt1.x - base.x, pt1.y - base.y);
	cv::Point vec2(pt2.x - base.x, pt2.y - base.y);

	float dot = vec1.x * vec2.x + vec1.y * vec2.y;
	return dot;
}

// function: 重排四边形的4个顶点，传入的[index]为第一个点，其余各点根据与第一个点的距离和角度依次排序
std::vector<cv::Point> ArrangeCorner(std::vector<cv::Point> approxCurve, int index)
{
	//内置一个结构体
	struct CornerDistance
	{
		float dist;
		int idx;
	};

	std::vector<cv::Point> sortedCurve;
	cv::Point baseCorner = approxCurve[index];

	std::vector<CornerDistance> corner_distances;
	for (int i = 0; i < approxCurve.size(); ++i)
	{
		if (i != index)
		{
			CornerDistance idx_dist;
			idx_dist.dist = calcEucdistance(baseCorner, approxCurve[i]);
			idx_dist.idx = i;

			corner_distances.push_back(idx_dist);
		}
	}

	//根据距离升序排序
	std::sort(corner_distances.begin(), corner_distances.end(),
		[](const CornerDistance& lhs, const CornerDistance& rhs) { return lhs.dist < rhs.dist; });

	//重排approxCurve的顺序 base点 - 短边点 - 长边点 - 对角线点
	sortedCurve.push_back(baseCorner);
	sortedCurve.push_back(approxCurve[corner_distances[0].idx]);

	const int _CorDist = 30;
	if (std::abs(corner_distances[1].dist - corner_distances[2].dist) < _CorDist)	//对角线和最长边距离差不多
	{
		//计算向量点积
		cv::Point Corner1 = approxCurve[corner_distances[0].idx];
		cv::Point Corner2 = approxCurve[corner_distances[1].idx];
		cv::Point Corner3 = approxCurve[corner_distances[2].idx];

		float dot1 = dot_product(baseCorner, Corner1, Corner2);
		float dot2 = dot_product(baseCorner, Corner1, Corner3);
		//两直线越接近90 dot(点积)越小
		if (dot1 < dot2)
		{
			sortedCurve.push_back(Corner2);
			sortedCurve.push_back(Corner3);
		}
		else
		{
			sortedCurve.push_back(Corner3);
			sortedCurve.push_back(Corner2);
		}
	}
	else
	{
		sortedCurve.push_back(approxCurve[corner_distances[1].idx]);
		sortedCurve.push_back(approxCurve[corner_distances[2].idx]);
	}

	return sortedCurve;
}

三、提取边缘中心点附近区域

如图所示：在拟合的四边形边长中心点依据每条直线的倾斜角度(angle)创建RotateRect，并以此作为掩模，提取边缘中心附近轮廓点作为最小二乘法拟合直线的数据。

1. 旋转矩形的生成

RotateRect()有一个构造函数，需要传入矩形中心点、旋转角度、Size大小，非常好用。

 /** full constructor
 @param center The rectangle mass center.
 @param size Width and height of the rectangle.
 @param angle The rotation angle in a clockwise direction. When the angle is 0, 90, 180, 270 etc.,the rectangle becomes an up-right rectangle.
 */
 RotatedRect(const Point2f& center, const Size2f& size, float angle);

根据拟合顶点我们可以轻松算出直线角度，旋转矩形的height取固定大小，width取顶点间距离的一半。

2.掩膜的制作

掩膜制作过程中，使用了一个很重要的函数fillPoly()用于多边形的填充，制作掩模的核心就在于此。再从边缘图像中根据掩膜区域提取对应区域，完整的代码如下：

class EdgeMask
{
public:
	EdgeMask(int height = 16, float width_ratio = 0.5): 
		rotate_rect_height(height), rotate_rect_width_ratio(width_ratio) { }

	//生成关于矩形每条边的mask
	std::vector<cv::Mat> make_RotateRectMask(std::vector<cv::Point> sortedcurve, cv::Mat& img);


private:
	//根据直线两端点，计算关于端点的中点的旋转矩形
	cv::RotatedRect RotateRectMask(cv::Point p1, cv::Point p2)
	{
		float angle = cv::fastAtan2((float)(p1.y - p2.y), (float)(p1.x - p2.x));

		cv::Point center;
		center.y = (p1.y + p2.y) / 2;
		center.x = (p1.x + p2.x) / 2;

		int rotate_rect_width = (int)calcEucdistance(p1, p2) * this->rotate_rect_width_ratio;

		cv::RotatedRect rotateRect(center, cv::Size(rotate_rect_width, rotate_rect_height), angle);

		return rotateRect;
	}

	//参数定义
	int rotate_rect_height = 16;
	float rotate_rect_width_ratio = 0.5;
};


std::vector<cv::Mat> EdgeMask::make_RotateRectMask(std::vector<cv::Point> sortedcurve, cv::Mat& img)
{
	std::vector<cv::RotatedRect> rotate_rect(4);
	rotate_rect[0] = RotateRectMask(sortedcurve[0], sortedcurve[1]);	// 1 - 2 construct short line
	rotate_rect[1] = RotateRectMask(sortedcurve[0], sortedcurve[2]);	// 1 - 3 construct long line
	rotate_rect[2] = RotateRectMask(sortedcurve[2], sortedcurve[3]);	// 2 - 4 construct short line
	rotate_rect[3] = RotateRectMask(sortedcurve[1], sortedcurve[3]);	// 3 - 4 construct long line

	std::vector<cv::Mat> rotate_rect_masks(4);
	for (int i = 0; i < rotate_rect.size(); ++i)
	{
		cv::Point2f vertices[4];
		rotate_rect[i].points(vertices);
		std::vector<cv::Point> vec_vertives(std::begin(vertices), std::end(vertices));
		std::vector<std::vector<cv::Point>> vec_vec_vertices = { vec_vertives };	//vec_vec 为fillpoly准备

		cv::Mat mask = cv::Mat::zeros(img.size(), CV_8UC1);
		cv::fillPoly(mask, vec_vec_vertices, cv::Scalar::all(255));

		cv::Mat dst;
		img.copyTo(dst, mask);

		rotate_rect_masks[i] = dst;
	}

	return rotate_rect_masks;
}

将每一条边的提取结果拼凑在一起进行可视化：

四、扑克牌顶点求取

1. 边缘轮廓点提取

每一边mask所提取的区域中，有可能会含有不是扑克牌边缘的干扰直线（内部图案边缘），但扑克牌边缘线的轮廓点数量是最多的，我们只需要对提取区域进行轮廓提取，保留最大轮廓即可完成边缘轮廓点的提取（当轮廓为一条线段时，findContours提取的轮廓点就是线段的组成像素点）。

2. 边缘直线交点

对提取的边缘轮廓点进行最小二乘法直线拟合，并定义求直线交点的函数：

//最小二乘法直线拟合
static cv::Vec4f _fit_edge_line(std::vector<cv::Point> linePoints)
{
	cv::Vec4f line;
	cv::fitLine(linePoints, line, cv::DIST_L2, 0, 0.01, 0.01);

	return line;
}


//两直线交点坐标
static cv::Point Line_intersection_coordinates(const cv::Vec4f& row_line, const cv::Vec4f& col_line)
{
	// 按道理应该先检查两直线的夹角情况  line(vx, vy, x0, y0)
	float k1 = row_line[1] / row_line[0];
	float k2 = col_line[1] / col_line[0];

	float x1 = row_line[2];
	float y1 = row_line[3];
	float x2 = col_line[2];
	float y2 = col_line[3];

	cv::Point intersection;
	intersection.x = (k1 * x1 - k2 * x2 + y2 - y1) / (k1 - k2);
	//intersection.y = k2 * (intersection.x - x2) + y2;
	// 试验发现y坐标应该使用推导式计算得到才会更加精确
	intersection.y = k1 * (k2 * (x1 - x2) + y2 - y1) / (k1 - k2) + y1;

	return intersection;
}

通过拟合4条直线求出了扑克牌的4个顶点，但这4个顶点的顺序进行透视变换可能无法将其变换到竖直状态，我们需要使用ArrangeCorner()函数重排顶点的顺序，但如何选取base点？

计算扑克牌长边直线与坐标系横轴的的夹角以此来判断当前扑克牌所处状态分为：左倾、右倾、竖直和水平，每种状态有不同的base点选取原则(根据顶点坐标)，只要确定了base点，就可以以唯一的顺序与变换后的点对应将其竖直校正回来。

// function: 根据masks求得扑克牌的4个角点
std::vector<cv::Point> PukeVertices(const std::vector<cv::Mat>& masks)
{
	//获得扑克牌真实的边缘直线 1-2, 1-3, 3-4, 2-4
	std::vector<std::vector<cv::Point>> edgeslines = Actual_line(masks);

	cv::Vec4f line1_2 = _fit_edge_line(edgeslines[0]);
	cv::Vec4f line1_3 = _fit_edge_line(edgeslines[1]);
	cv::Vec4f line3_4 = _fit_edge_line(edgeslines[2]);
	cv::Vec4f line2_4 = _fit_edge_line(edgeslines[3]);

	// 1-2-3, 1-2-4, 1-3-4, 2-3-4
	std::vector<cv::Point> vectices(4);

	//1-2 -- 1-3 --> intersection point
	vectices[0] = Line_intersection_coordinates(line1_2, line1_3);

	//1-2 -- 2-4 --> intersection point
	vectices[1] = Line_intersection_coordinates(line1_2, line2_4);

	//1-3 -- 3-4 --> intersection point
	vectices[2] = Line_intersection_coordinates(line1_3, line3_4);

	//2-4 -- 3-4 --> intersection point
	vectices[3] = Line_intersection_coordinates(line2_4, line3_4);

	//***************************用1-3来确定扑克牌方向********************************//
	float angle = cv::fastAtan2(line1_3[1], line1_3[0]);
	std::cout << "puke angle = " << angle << std::endl;

	std::vector<int> addpoints(4), subpoints(4), points_x(4), points_y(4);
	for (int i = 0; i < 4; ++i)
	{
		addpoints[i] = vectices[i].x + vectices[i].y;
		subpoints[i] = vectices[i].x - vectices[i].y;
		points_x[i] = vectices[i].x;
		points_y[i] = vectices[i].y;
	}

	if ((angle > 80 && angle <= 100) || (angle > 260 && angle <= 280))	//竖直状态
	{
		//min(x + y) --> top_point
		auto min_iter = std::min_element(addpoints.begin(), addpoints.end());
		int top_idx = (int)(min_iter - addpoints.begin());

		vectices = ArrangeCorner(vectices, top_idx);
	}
	else if (angle > 350 || angle <= 10 || (angle > 170 && angle <= 190))	//水平状态
	{
		//min(x - y) --> top_point
		auto min_iter = std::min_element(subpoints.begin(), subpoints.end());
		int top_idx = (int)(min_iter - subpoints.begin());

		vectices = ArrangeCorner(vectices, top_idx);
	}
	else if ((angle > 100 && angle <= 170) || (angle > 280 && angle <= 350))	// 右斜
	{
		//min(y) --> top_point
		auto min_iter = std::min_element(points_y.begin(), points_y.end());
		int top_idx = (int)(min_iter - points_y.begin());

		vectices = ArrangeCorner(vectices, top_idx);
	}
	else if ((angle > 10 && angle <= 80) || (angle > 190 && angle <= 260))		//左倾
	{
		//min(x) --> top_point
		auto min_iter = std::min_element(points_x.begin(), points_x.end());
		int top_idx = (int)(min_iter - points_x.begin());

		vectices = ArrangeCorner(vectices, top_idx);
	}

	return vectices;
}

五、透视变换

扑克牌的尺寸标准是6.3x8.8cm，将校正后图像尺寸大小设置为（630，880），将变换前与变换后的顶点对应应用透视变换即可完成校正。

//function: 根据排好序的四边形顶点进行透视变换
void puke_perspectiveTransform(const std::vector<cv::Point> vectices, const cv::Mat& src, cv::Mat& dst)
{
	//puke standerd size = (6.3cm X 8.8cm)
	dst = cv::Mat::zeros(cv::Size(630, 880), CV_8UC3);

	cv::Point2f src_pts[4] = { vectices[0], vectices[1], vectices[2], vectices[3] };
	cv::Point2f dst_pts[4] = { cv::Point2f(0, 0), cv::Point2f(dst.cols - 1, 0),
						   cv::Point2f(0, dst.rows - 1), cv::Point2f(dst.cols - 1, dst.rows - 1) };

	cv::Mat M = cv::getPerspectiveTransform(src_pts, dst_pts, cv::DECOMP_SVD);
	cv::warpPerspective(src, dst, M, dst.size());
}

测试案例

多视角校正是没有发现问题的，但是还是存在一点点小瑕疵，这个与扑克牌是不是平整的有很大的关系，当扑克牌有翘曲，其边缘就不是一条直线了而是曲线，这种情况下的校正就有一定难度了，而且具有一定的商业价值，就不在网上做分享记录了…