MATLAB中FFT的分析总结
1、采样频率和采样周期的设定:
采样频率的设定应满足奈奎斯特准则,当采样频率设定之后求倒数即为采样周期。
如:
Fs = 1000; % Sampling frequency 采样频率
T = 1/Fs; % Sampling period 采样周期
2、采样点数的确定:
– 若想要规定采样点数,则采用如下方式:
L = 1000; % Length of signal 对信号的采样点数
t = (0:L-1)*T; % Time vector 采样的时间点序列
–若想要规定时间范围则采用如下方式:
t = -5:T:5;
L = length(t);
3、频率的分辨率:
时域的采样频率决定了频域的最大值(fmax=fs),所以在已知信号的时域采样率后,可得频率域的分辨率ff,即ff=fs/N. 其中N为做FFT的点数,可以根据分辨率的需要来自行设定,在没有输入N的情况下系统默认为信号时域的采样点数L!但是注意设定的N值要产生的最小分辨率要小于被分析信号频率间的最小差值,要不然会失真!
如:
–不输入N时,fft(X)中N默认为为采样点数L。
–输入N时,fft(X,N)即对X做N(可自由设定)点fft。 N值虽可以自由设定,但N值越小,频率分辨率越大,当频率分辨率大于信号最小频率分量时,得到的频谱会失真。
4、频率轴的处理
频率轴的归一化:
经过N点FFT得到的频谱被分成N份范围为[0 fs],不是真实的频域。要想获得真正的频率轴,需要对频率轴进行归一化处理:
f = Fs*(0:(N-1))/N;
频率轴归一化之后做平移(利用fftshift())使其关于0对称:
做完fft之后在做fftshift(),同时对频率轴进行归一化和平移处理
Y = fft(X);
Y1 = fftshift(Y);
f = Fs*(((-L)/2):(L/2-1))/L;
参考代码:
clc;
clear;
close;
%% 注释
% MATLAB_help注释 + 个人理解注释
Fs = 1000; % Sampling frequency 采样频率
T = 1/Fs; % Sampling period 采样周期
% 根据需要设定L和t序列;想要确定采样点数则用方式1;想要确定时间范围则用方式2
% L = 1000; % Length of signal 对信号的采样点数
% t = (0:L-1)*T; % Time vector 采样的时间点序列
t = -5:T:5;
L = length(t);
%% 对信号进行采样
S = 0.7sin(2pi50t) + sin(2pi120t);
X = S + 1randn(size(t));
%% 对采样信号做一系列FFT处理 fft(x)默认做L点的FFT,L为采样点数
figure(1);
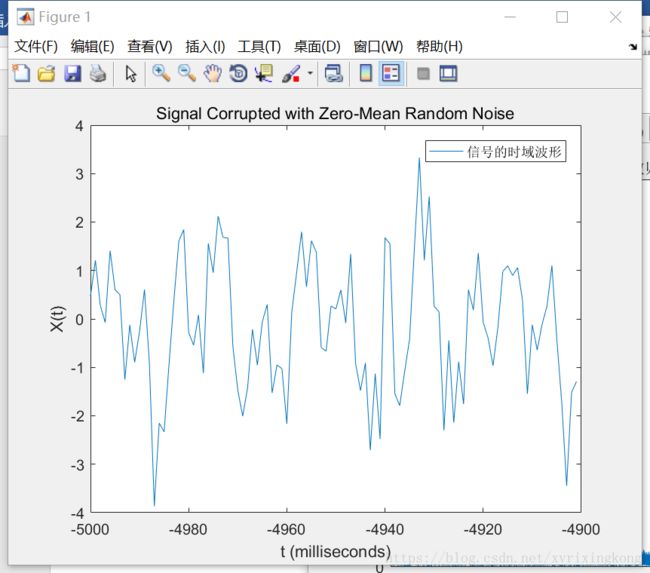
plot(1000*t(1:100),X(1:100))
title(‘Signal Corrupted with Zero-Mean Random Noise’)
xlabel(‘t (milliseconds)’)
ylabel(‘X(t)’)
% 对加噪声信号做FFT
Y = fft(X);
Y1 = fftshift(Y);
figure(2)
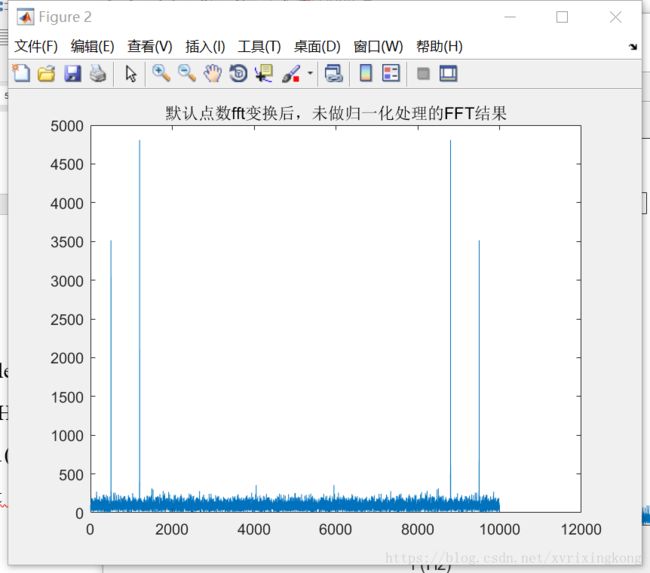
plot(abs(Y))
title(‘未做归一化处理的FFT结果’)
P2 = abs(Y/L);
f = Fs*(0:(L-1))/L;
figure(3);
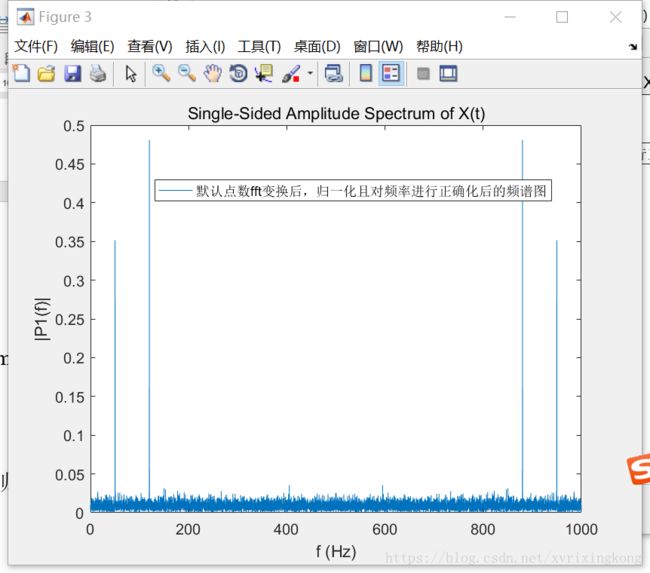
plot(f,P2)
title(‘Single-Sided Amplitude Spectrum of X(t)’)
xlabel(‘f (Hz)’)
ylabel(’|P1(f)|’)
legend(‘fft变换后,归一化且对频率进行正确化后的频谱图’);
P1 = P2(1:L/2+1);
% P1(2:end-1) = 2P1(2:end-1);
f = Fs(0:(L/2))/L;
figure(4);
plot(f,P1)
title(‘Single-Sided Amplitude Spectrum of X(t)’)
xlabel(‘f (Hz)’)
ylabel(’|P1(f)|’)
legend(‘fft变换后,归一化且对频率进行正确化后,取一半的 频谱图’);
f = Fs*(((-L)/2):(L/2-1))/L;
figure(5);
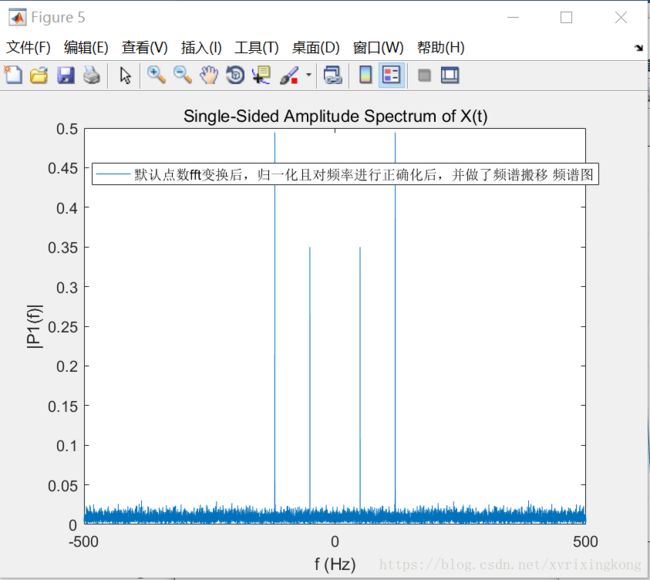
plot(f,abs(Y1)/L)
title(‘Single-Sided Amplitude Spectrum of X(t)’)
xlabel(‘f (Hz)’)
ylabel(’|P1(f)|’)
legend(‘fft变换后,归一化且对频率进行正确化后,并做了频谱搬移 频谱图’);
%% 对采样信号做一系列N点的FFT处理 fft(x,N)
N = 128;
y1 = fft(X,N);
y1 = abs(y1)/N;
f = Fs*(0:(N-1))/N;
plot(f,y1)
title(‘Single-Sided Amplitude Spectrum of X(t)’)
xlabel(‘f (Hz)’)
ylabel(’|P1(f)|’)
为了便于显示,仅取时域波形的一段进行显示。
从图中可以看出,未做归一化处理之前,纵轴值很大,横轴对应着fft的点数。
从图中可以看出,归一化处理之后,频谱图的范围为[0 fs],但实际的频谱范围应该为[-fs/2 fs/2],所以还需要做一下平移,如下图所示。
当进行N点fft时,N过小时会使频谱图失真,如下图所示。
参考网址:
【Matlab中fft的正确简单理解】http://blog.sina.cn/dpool/blog/s/blog_166c28bd30102x7dg.html
【Matlab fftshift 详解】https://blog.csdn.net/myathappy/article/details/51344618