随机森林分类器

---

前言

随机森林是非常具有代表性的Bagging（装袋法）集成算法，它的所有基评估器都是决策树，分类树组成的森林就叫做随机森林分类器（RandomForestClassifier）。

---

一、重要参数

1.1 控制基评估器的参数

参数	含义
criterion	不纯度的衡量指标，有基尼系数和信息熵两种选择
max_depth	树的最大深度，超过最大深度的树枝都会被剪掉
min_samples_leaf	一个节点在分枝后的每个子节点都必须包含至少min samples leaf个训练样本，否则分枝就不会发生
min_samples_split	一个节点必须要包含至少min_samples_split个训练样本，这个节点才允许被分枝，否则分枝就不会发生
max_features	限制分枝时考虑的特征个数，超过限制个数的特征都会被舍弃，默认值为总特征个数开平方取整
min_impurity_decrease	限制信息增益的大小，信息增益小于设定数值的分枝不会发生

这些参数在随机森林中的含义，和我们在上决策树时说明的内容一模一样，单个决策树的准确率越高，随机森林的准确率也会越高，因为装袋法是依赖于平均值或者少数服从多数原则来决定集成的结果的。

---

1.2 n_esitmators

这是森林中树木的数量，即基评估器的数量

n_estimators越大，模型的效果往往越好。但是相应的，任何模型都有决策边界，n_estimators达到一定的程度之后，随机森林的精确性往往不在上升或开始波动，并且，n_estimators越大，需要的计算量和内存也越大，训练的时间也会越来越长。

n_estimators的默认值在现有版本的sklearn中是10，但是在即将更新的0.22版本中，这个默认值会被修正为100。这个修正显示出了使用者的调参倾向：要更大的n_estimators，取值不应超过200。

---

1.2.1 建立森林

树模型的优点是简单易懂，可视化之后的树人人都能够看懂，随机森林是无法被可视化。所以为了更加直观地让大家体会随机森林的效果，我们来进行一个随机森林和单个决策树效益的对比。我们依然使用红酒数据集。

1.导入需要的包

%matplotlib inline
from sklearn.tree import DecisionTreeClassifier #分类树
from sklearn.ensemble import RandomForestClassifier #随机森林在ensemble模块下，这里是分类器
from sklearn.datasets import load_wine #红酒数据集
from sklearn.model_selection import train_test_split #划分测试集与分类集
from sklearn.model_selection import cross_val_score #交叉验证
import matplotlib.pyplot as plt

2.导入需要的数据集

wine = load_wine()

wine.data #查看特征
wine.target # 标签

3.复习:sklearn建模的基本流程

Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data,wine.target,test_size=0.3)#划分测试集和训练集
clf = DecisionTreeClassifier(random_state=0) #随机森林分类器实例化
rfc = RandomForestClassifier(random_state=0) #分类树实例化
clf = clf.fit(Xtrain,Ytrain)#模型训练
rfc = rfc.fit(Xtrain,Ytrain)#模型训练
score_c = clf.score(Xtest,Ytest)#得出评估分数
score_r = rfc.score(Xtest,Ytest)#得出评估分数

print(f'Single Tree:{score_c}   Random Forest:{score_r}')

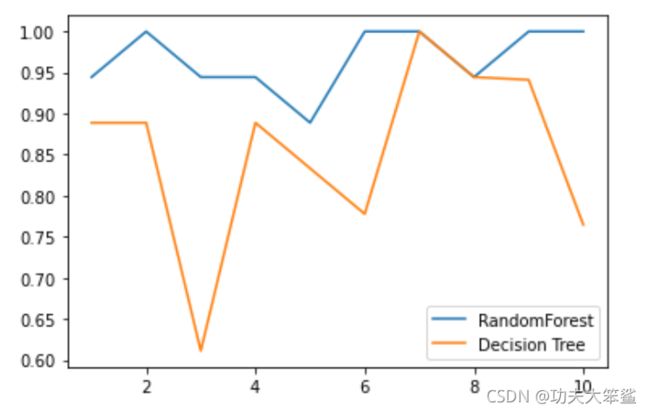
4 . 画出随机森林和决策树在一组交叉验证下的效果对比

rfc = RandomForestClassifier(n_estimators=25)#实例化，设置森林有25个树
rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10)#做10次交叉验证
clf = DecisionTreeClassifier(random_state=10)#实例化
clf_s = cross_val_score(clf,wine.data,wine.target,cv=10)#10次交叉验证
plt.plot(range(1,11),rfc_s,label = "RandomForest")
plt.plot(range(1,11),clf_s,label = "Decision Tree")
plt.legend()
plt.show()

这种写法和上面得到的结果相同

#通过循环的方法
label = "RandomForest"
for model in [RandomForestClassifier(n_estimators=25),DecisionTreeClassifier(random_state=10)]:
   score = cross_val_score(model,wine.data,wine.target,cv=10)
   plt.plot(range(1,11),score,label = label)
   plt.legend()
   label = "DecisionTree"

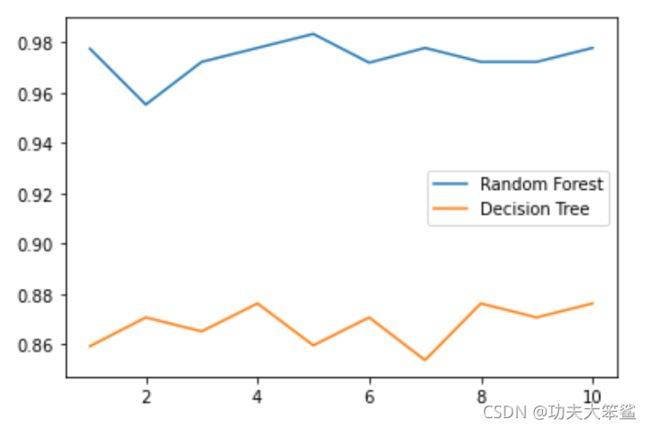
5.画出随机森林和决策树在十组交叉验证下的效果对比

rfc_1 = []
clf_1 = []
for i in range(10):
    rfc = RandomForestClassifier(n_estimators=25)
    rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10).mean()#将十次的交叉验证取平均值作为当前森林的评估值
    rfc_1.append(rfc_s)
    
    clf = DecisionTreeClassifier()
    clf_s = cross_val_score(clf,wine.data,wine.target,cv=10).mean()#将十次的交叉验证取平均值作为当前分类树的评估值
    clf_1.append(clf_s)
    
plt.plot(range(1,11),rfc_1,label='Random Forest')
plt.plot(range(1,11),clf_1,label='Decision Tree')
plt.legend()
plt.show()

• 单个决策树的波动轨迹和随机森林一致，不一致的情况是特殊情况，训练集和测试集划分的原因
• 再次验证了，单个决策树的准确率越高，随机森林的准确率也会越高

6.n_estimators的学习曲线

superpa = []
#在200之内最好
for i in range(200):
    rfc = RandomForestClassifier(n_estimators=i+1)
    rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10).mean()
    superpa.append(rfc_s)
    
print(max(superpa),superpa.index(max(superpa)))
plt.figure(figsize=[20,5])
plt.plot(range(1,201),superpa)
plt.show()

---

1.3 random_state

随机森林的本质是一种装袋集成算法（bagging），装袋集成算法是对基评估器的预测结果进行平均或用多数表决原则来决定集成评估器的结果。

在刚才的红酒例子中，我们建立了25棵树，对任何一个样本而言，平均或多数表决原则下，当且仅当有13棵以上的树判断错误的时候，随机森林才会判断错误。单独一棵决策树对红酒数据集的分类准确率在0.85上下浮动，假设一棵树判断错误的可能性为0.2(ε)，那13棵树以上都判断错误的可能性是:
$$e_{rando{m}_{f}orest}=\sum _{i=13}^{25}{C}_{25}^i{\epsilon }^i(1-\epsilon {)}^{25-i}=0.000369$$
i是判断错误的次数，也是判错的树的数量，ε是一棵树判断错误的概率，（1-ε）是判断正确的概率，共判对25-i次。采用组合，是因为25棵树中，有任意i棵都判断错误。

随机森林在红酒数据集上的表现远远好于单棵决策树。
对上述公式可以用代码来计算：

import numpy as np
from scipy.special import comb# comb为组合，scipy用来配合计算numpy等
np.array([comb(25,i)*(0.2**i)*((1-0.2)**(25-i)) for i in range(13,26)]).sum()

那现在就有一个问题了：我们说袋装法服从多数表决原则或对基分类器结果求平均，这即是说，我们默认森林中的每棵树应该是不同的，并且会返回不同的结果。设想一下，如果随机森林里所有的树的判断结果都一致（全判断对或全判断错），那随机森林无论应用何种集成原则来求结果，都应该无法比单棵决策树取得更好的效果才对。但我们使用了一样的类DecisionTreeClassifier，一样的参数，一样的训练集和测试集，为什么随机森林里的众多树会有不同的判断结果？

sklearn中的分类树DecisionTreeClassifier自带随机性，所以随机森林中的树天生就都是不一样的。在学习分类树时曾提到，决策树从最重要的特征中随机选择出一个特征来进行分枝，因此每次生成的决策树都不一样，这个功能由参数random_state控制。

随机森林中其实也有random_state，用法和分类树中相似，只不过在分类树中，一个random_state只控制生成棵树，而随机森林中的random_state控制的是生成森林的模式，而非让一个森林中只有一棵树。

rfc = RandomForestClassifier(n_estimators=20,random_state=2)
rfc = rfc.fit(Xtrain, Ytrain)

通过1.4中estimators属性可以观察到，当random_state固定时，随机森林中生成是一组固定的树，但每棵树依然是不一致的，这是用”随机挑选特征进行分枝“的方法得到的随机性。并且我们可以证明，当这种随机性越大的时候，袋装法的效果一般会越来越好。用袋装法集成时，基分类器应当是相互独立的，是不相同的。

• 但这种做法的局限性是很强的，当我们需要成千上万棵树的时候，数据不一定能够提供成千上万的特征来让我们构筑尽量多尽量不同的树。因此，除了random_state。我们还需要其他的随机性。

---

1.4 重要属性之一：estimators，查看森林中树的情况

rfc.estimators_[0].random_state#打出森林中第一颗树的random_state
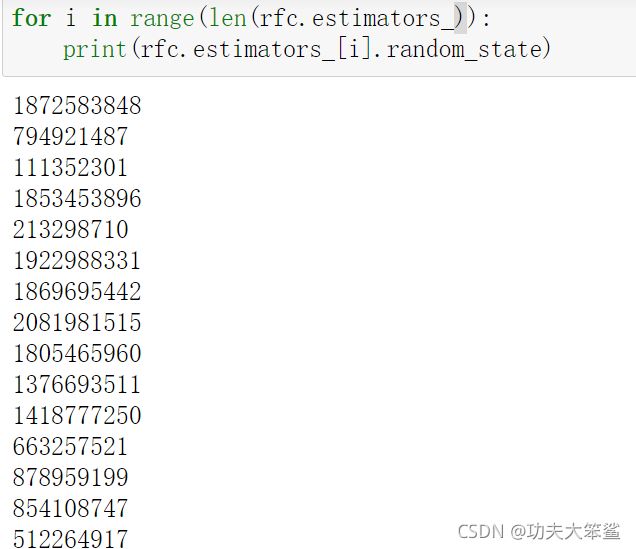
for i in range(len(rfc.estimators_)):#循环打出森林中所有的树的random_state
    print(rfc.estimators_[i].random_state)

---

1.5 bootstrap & oob_score

bootstrap

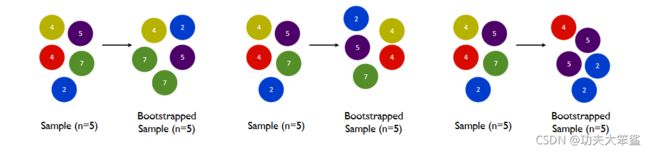
要让基分类器尽量都不一样，一种很容易理解的方法是使用不同的训练集来进行训练，而袋装法正是通过有放回的随机抽样技术来形成不同的训练数据，bootstrap就是用来控制抽样技术的参数。

在一个含有n个样本的原始训练集中，我们进行随机采样，每次采样一个样本，并在抽取下一个样本之前将该样本放回原始训练集，也就是说下次采样时这个样本依然可能被采集到，这样采集n次，最终得到一个和原始训练集一样大的，n个样本组成的自助集。由于是随机采样，这样每次的自助集和原始数据集不同，和其他的采样集也是不同的。这样我们就可以自由创造取之不尽用之不竭，并且互不相同的自助集，用这些自助集来训练我们的基分类器，我们的基分类器自然也就各不相同了。

bootstrap参数默认True，代表采用这种有放回的随机抽样技术。通常，这个参数不会被我们设置为False

oob_score

然而有放回抽样也会有自己的问题。由于是有放回，一些样本可能在同一个自助集中出现多次，而其他一些却可能被忽略，一般来说，自助集大约平均会包含63%的原始数据。因为每一个样本被抽到某个自助集中的概率为：
$$1-(1-\frac{1}{n}{)}^n$$
当n足够大时，这个概率收敛于1-(1/e)，约等于0.632。因此，会有约37%的训练数据被浪费掉，没有参与建模，这些数据被称为袋外数据(out of bag data，简写为oob)。除了我们最开始就划分好的测试集之外，这些数据也可以被用来作为集成算法的测试集。也就是说，在使用随机森林时，我们可以不划分测试集和训练集，只需要用袋外数据来测试我们的模型即可。当然，这也不是绝对的，当n和n_estimators都不够大的时候，很可能就没有数据掉落在袋外，自然也就无法使用oob数据来测试模型了。

如果希望用袋外数据来测试，则需要在实例化时就将oob_score这个参数调整为True

rfc = RandomForestClassifier(n_estimators=25,oob_score=True)
rfc = rfc.fit(wine.data,wine.target)#不需要划分测试集和训练集，oob_score=True会使用袋外数据来当测试集

---

1.6 重要属性之一： 使用oob_score_来查看模型在袋外数据上的测试结果

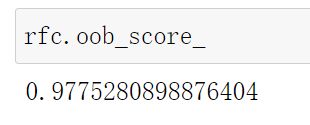
上方训练完毕后训，我们可以用随机森林的另一个重要属性：oob_score_来查看我们的模型在袋外数据上测试的结果：

rfc.oob_score_

---

二、重要属性和接口

重要属性

• .estimators_：详细使用看1.4
• .oob_score_：详细使用看1.6
• 作为树模型的集成算法，随机森林自然也有.feature_importances_这个属性（在分类树有详细介绍）

接口

随机森林的接口与决策树完全一致

• apply
• fit
• predict
• score

随机森林

• predict_proba：返回每个测试样本对应的被分到每一类标签的概率，标签有几个分类就返回几个概率。
  

如果是二分类问题，则predict_proba返回的数值大于0.5的，被分为1，小于0.5的，被分为0。传统的随机森林是利用袋装法中的规则，平均或少数服从多数来决定集成的结果，而sklearn中的随机森林是平均每个样本对应的predict_proba返回的概率，得到一个平均概率，从而决定测试样本的分类

rfc = RandomForestClassifier(n_estimators=25)
rfc = rfc.fit(Xtrain, Ytrain)
rfc.score(Xtest,Ytest)
rfc.feature_importances_
rfc.apply(Xtest)
rfc.predict(Xtest)
rfc.predict_proba(Xtest)

---

三、Bagging（装袋法）的另一个必要条件

在开头提到在使用袋装法时要求基评估器要尽量独立。其实，袋装法还有另一个必要条件：基分类器的判断准确率至少要超过随机分类器，即是说，基分类器的判断准确率至少要超过50%。之前我们已经展示过随机森林的准确率公式，基于这个公式，我们画出了基分类器的误差率ε和随机森林的误差率之间的图像。大家可以自己运行一下这段代码，看看图像呈什么样的分布

import numpy as np
x = np.linspace(0,1,20) y = []
for epsilon in np.linspace(0,1,20):
    E = np.array([comb(25,i)*(epsilon**i)*((1-epsilon)**(25-i)) 
                  for i in range(13,26)]).sum()
    y.append(E)
plt.plot(x,y,"o-",label="when estimators are different")
plt.plot(x,x,"--",color="red",label="if all estimators are same")
plt.xlabel("individual estimator's error")
plt.ylabel("RandomForest's error")
plt.legend()
plt.show()

可以从图像上看出，当基分类器的误差率小于0.5，即准确率大于0.5时，集成的效果是比基分类器要好的。相反，当基分类器的误差率大于0.5，袋装的集成算法就失效了。所以在使用随机森林之前，一定要检查，用来组成随机森林的分类树们是否都有至少50%的预测正确率。

---

总结

随机森林建立于决策树的基础上，下面是决策树学习笔记
决策树概论