t检验，单因素方差和相似非参数检验-IBM SPSS 第六版第9章译文

本部分译文目的是尽量避免在使用SPSS时，知其然不知其所以然，或者甚至是不尽知其然的情况，在分析时经常会被问到该用什么哪种检验，就自行翻译一下这本书的第9章。

声明：此翻译非正式翻译，仅为个人翻译供大家学习参考用，尊重知识，请务必不要传播。

《IBM SPSS for Introductory Statistics Use and Interpretation》
作者：
George A. Morgan，科罗拉多州立大学教育和人类发展名誉教授。
Karen C. Barrett，科罗拉多州立大学人类发展和家庭研究教授。
Nancy L. Leech，科罗拉多大学研究和评估方法教授。
Gene W. Gloeckner，前IRB主席，前教育学院院长。

我下载的电子书是第六版，应该到现在为止是最新版本。

正文
在本章中，我们将讨论用于比较群体的不同统计数据。
首先，在问题9.1中，我们将使用单样本 t 检验来比较一个组或样本与假设的群体平均值。
然后，在问题9.2-9.5中，我们将研究两个参数统计和两个非参数/ordinal统计，以比较两组参与者。问题9.2使用独立样本 t 检验，对两个独立组（组间设计），即快速通道的学生和普通通道的学生进行比较。问题9.3使用曼-惠特尼非参数检验，它与独立 t 检验相似，但在不符合独立 t 检验的假设条件时使用。问题9.4是一个科目内设计，使用配对样本 "来比较学生的母亲和父亲的平均或平均教育水平。问题9.5显示了如何使用非参数的Wilcoxon检验来进行被试内设计。

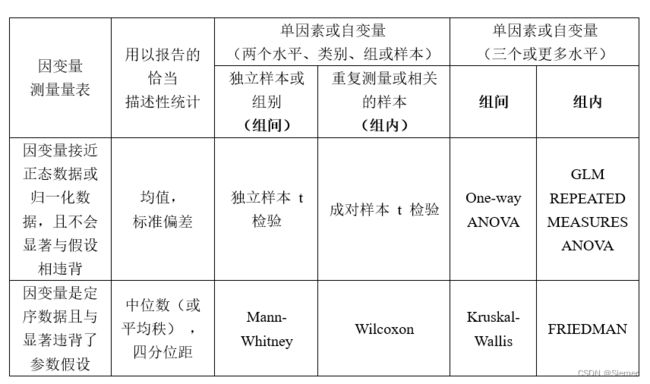
表9.1的右上方区分了组间设计和被试内设计。这有助于确定要使用的具体统计数字。使用哪种统计量的另一个决定因素与统计假设有关。如果没有明显违反假设，你可以使用参数检验，如 t 检验或方差分析。如果假设被明显违反，就可以使用非参数检验，这种检验没有相同的假设，如表9.1底行左侧所示。
另一种方法是对变量进行转换，使其符合假设。这超出了本书的范围，但在Leech等人（2015）中有所涉及。

在本章后面，你将学习 ANalysis Of VAriance，ANOVA（F），即方差分析，它可以用来考察两组或多组的平均值之间的差异。
你可能会问，既然 ANOVA 可以用来比较两组以及三组或更多组，为什么还要计算 t 检验呢？因为 $F=t^2$ ，这两个统计量提供了相同的信息。因此，选择主要是个人偏好的问题。然而，t 检验可以是单尾，也可以是双尾的，而方差分析的统计量，通常都是跟某个指定的值比较大小，没有单尾这一说。因此，如果你有一个明确的指向性假设，预测哪一组的平均值更高，那么在比较两组时，你可能想使用 t 检验，而不是方差分析。此外，t 检验输出提供了处理不等方差问题的调整，而方差分析中对这种问题的补救可能不太令人满意。最后，如果只对两组进行比较，使用 t 检验是比较习惯的。如果你想比较三个或更多的组，你必须使用方差分析。

你将学习如何计算两种类型的方差分析（ANOVA）和类似的非参数统计。
在问题9.6中，我们将使用单因素方差分析来比较父亲在几个因变量（例如，数学成绩）上的三个教育水平。如果方差分析具有统计学意义，你就会知道某处存在差异，但你不会知道具体哪几对均值存在显著差异。
在问题9.7中，我们将向您展示何时以及如何进行适当的事后检验post hoc tests，以了解哪对均值有差异。
在问题9.8中，您将计算 Kruskal-Wallis（K-W）检验，这是一种类似于单因素方差分析的非参数检验。
在问题9.9中，我们将向您介绍双向或因子方差分析factorial ANOVA，但在表9.1中没有显示。表9.2显示了如何解释本章中使用的效应大小测量方法。

表9.1 为基本的双变量差异问题或假设选择一个适当的推断统计方法

【9.1 单样本 t 检验很简单就放到最后再翻译】
**

Problem 9.2 独立样本 t 检验

**
当调查由近似正态的因变量构成的两个不相关的或独立的组别之间的差异时，如果没有明显违反以下假设，选择独立样本 t 检验是合适的。

独立样本 t 检验的假设：

1. 两组中因变量的方差（也即标准偏差的平方）是相等的。
2. 每个组别内的样本满足正态分布
3. 数据是相互独立的

SPSS会自动用 Levene’s Test 来检验假设1的方差齐性。假设2可以像我们在第四章问题4.3中所做的那样，用 Explore 命令来检验，看因变量是否至少是近似正态分布。因为 t 检验对违反这一假设的情况相当稳健，特别是在两组数据都偏斜的情况下。因为 "检验 "对违反这一假设的情况相当稳健，尤其是在两组数据都向同一方向出现偏态分布的情况下，故我们在此不作检验。假设3最好在设计和数据收集期间解决。
除了确保数据符合这些假设外，研究者还应该尽量确保小样本组大小相似，因为方差同质性的假设是最重要的，如果样本规模有明显的差异，不满足此假设的可能性就更大。

9.2. 快班和普通班学生在平均数学成绩、高中成绩和可视化测试成绩方面有差异吗?
这个SPSS项目的特征之一是它可以在一项单独的输出中做一些 t 检验，如果他们有相同的独立或组别变量。
在这个问题中，我们计算了三个 t 检验，分别用来检验平均数学成绩、高中成绩和可视化测试成绩，每一个检验中，快班和普通班的学生都进行对比。

如果有一个以上的因变量，人们可以选择使用 MANOVA（见图5.1）。特别是如果这些变量在概念上是相关的，并且相互之间有关联。MANOVA 将使我们能够看到这三个变量的线性组合对快班和普通班学生有什么不同。我们不会在本书中演示 MANOVA，但关于如何计算和解释 MANOVA，请参见Leech等人（2015）的 IBM SPSS中级统计（第五版）。

对于 t 检验，请参考以下命令进行操作：

1. 点击分析-比较均值-独立样本 t 检验…
2. 将数学成绩，高中成绩和可视化测试成绩放入检验变量一栏，将班级分类放入分组变量一栏
   
3. 点击定义组
4. 在组1输入0，组2输入1，这样可以从三个因变量上分别对比快班和普通班学生
5. 点击 继续-OK
   
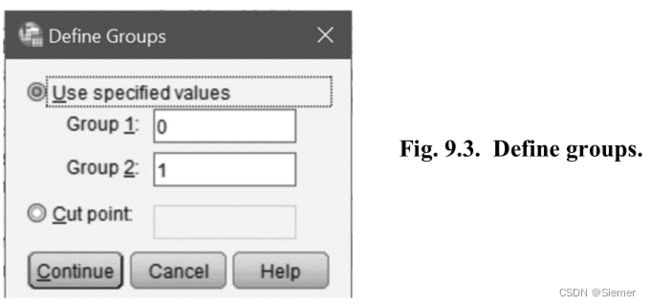
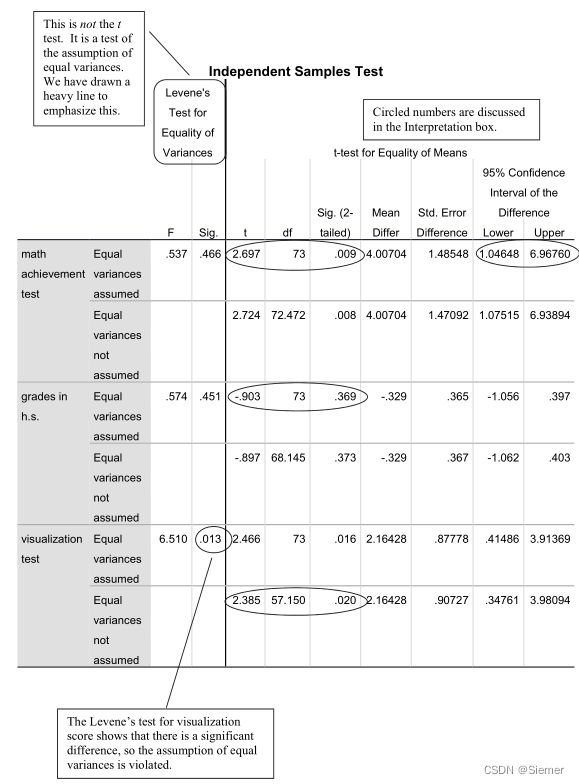
   输出结果如下图所示，注意图例的 Levene 检验结果一栏，原假设是方差没有显著差异，即方差齐性，最后一组 Levene 检验的 p = 0.013，说明拒绝原假设，也即不满足方差齐性的前提。
   

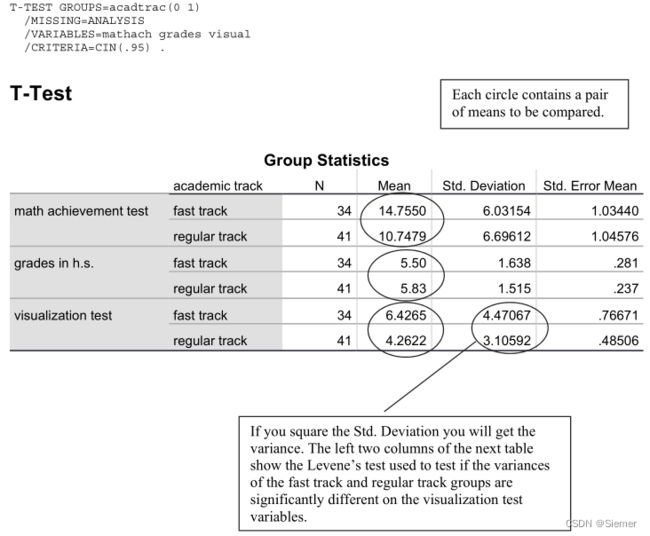
Problem 9.3 非参数 Mann-Whitney U 检验

如果数据明显违反了 t 检验的前提假设（例如，如果因变量数据呈明显的偏态分布、或非正态分布，或数据是定序数据），你应该怎么做？一个答案是采用适当的非参数统计，在这种情况下，它被称为曼-惠特尼（M-W）U检验。M-W检验适用于自变量有两个水平的组间设计。“The M–W is used with a between-groups design with two levels of the independent variable.”

9.3 快班和普通班学生在可视化、数学成绩和年级上是否有差异？

针对这个问题，我们假定三种因变量的得分是定序数据，或者违背了 t 检验的其它前提假设，但满足M-W 检验的假设。

Mann–Whitney Test 假设

1. 在排名之前，假设因变量的分数从低到高排序。
2. 数据是相互独立的。（一个参与者的得分不依赖于其它人的得分）

分析步骤：

1. 点击分析-非参数检验-对话框-2个独立样本
2. 将可视化测验，数学成绩和年级放入检验变量列表
3. 点击分班组别（自变量）并放入分组变量
4. 点击定义组别-分别输入0和1代表快班和普通班
5. 保证M-W U检验，窗口应该如下图所示

最后点击OK

非参数检验输出结果


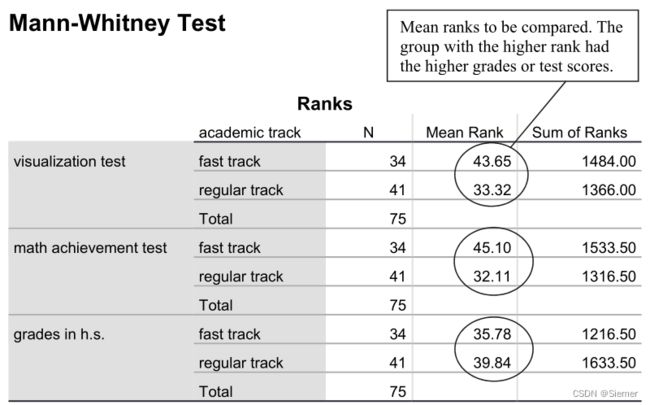
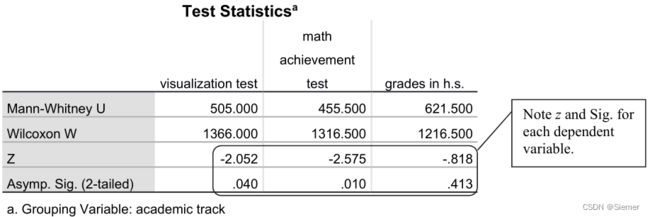
注意：
Asymptotic (“Asymp.”) significance refers to the fact that the significance levels are not exact. 即表格中的渐进显著性表示这个显著性并不是确切的。
Mann-Whitney相较于 t 检验是较为有利的证据，在数据违背 t 检验的前提假设下，M-W检验是一种较好的替换选择检验方法，但注意对同相同变量进行的 t 检验和M-W检验结果只能报告一种，因为两者的检验结果有时会提供出非常近似的信息。

更新至20220606