python数据分析及可视化(一)课程介绍以及统计学的应用、介绍、分类、基本概念及描述性统计
数据分析及可视化介绍
这门课涉及多个库,其中Numpy用于数值运算;Pandas用于数据处理;Matplotlib、Seaborn、Pyecharts用于数据可视化。
数据分析介绍
概念
用适当的统计分析方法对收集来的大量数据进行分析;提取有用信息和形成结论;对数据加以详细研究和概括总结的过程。数据分析的核心就是数据,拿到的数据不能直接使用,通过数据清洗,去除无用、杂乱的数据,提取有用的信息,得到结论,侧重于整个分析的过程。
流程
明确目的—>准备数据—>数据解析—>分析数据—>获得结论—>成果可视化
根据数据分析目的的不同,可以分为三种,现状分析、原因分析、预测分析。现状分析是告诉你过去发生了什么,为什么会导致这个现状,如通过数据分析,了解电商平台的用户画像,为电商企业做客户的留存率等指标分析,进而帮助平台进行产品化的运营;原因分析是告诉你这个现状为什么会发生,如屏蔽垃圾邮件,邮件服务器根据邮件的内容对邮件进行归类;预测分析是根据现有的状况,在现有合理数据的基础上,预测未来可能要发生的趋势和事情,如预测股票、比特币的涨幅趋势。
数据分析和数据挖掘
相似:都是对数据进行分析、处理等操作
区别:1.在应用工具上,数据分析是借助现有的分析工具进行,数据挖掘一般都要通过编程来实现;
2.在行业知识方面,数据分析要求对所从事的行业有比较深的了解,更多的是将数据和业务联系起来,数据挖掘则不需要太多的行业知识,更专注于技术层面。
Jupyter Notebook介绍
开源的网络应用,可以用于创建和共享代码与文档,可以在其中编写代码、运行代码、查看输出、可视化数据并查看结果,是一款可执行端到端的数据科学工作流程的便捷工具,其中包括数据清理、统计建模、构建和训练机器学习模型、可视化数据等等。
Jupyter Notebook特点
1.支持Markdown语法
2.分块执行代码
3.直接输出变量
4.智能Tab键提示
5.查看源码,方法后加问好,运行就可以
6.表格数据交互显示
7.可视化图表显示
Jupyter Notebook使用
pip install jupyter
如何运行 Jupyter Notebook?
1.首先需要建立单独项目文件夹(建议名称不要包含中文)
2.windows+R输入cmd进入windows终端
3.切换到该文件夹路径下,盘符:切换盘符,cd + 文件夹路径 切换到当前盘符下的路径
4.打开命令:jupyter notebook
统计学
数据分析、机器学习跟统计学是分不开的。概率论与数理统计更加倾向于数学的内容,有大量的公式和推到;统计学更加侧重于概念性的解释。概率论是统计学的基础。
统计学的应用
1.连续玩了10把猜大小的游戏,10把开的都是"大"。接下来,大家是继续猜"大"?还是加倍压"小"呢?
要避免进入小数陷阱,大和小出现的概率都是一样的,都是50%,它们两者之间没有任何的关系,两者是独立并随机的。有人说前面都是出的大,后面出小的概率很大,我前面没有猜中,后面一定会猜中,这其实是赌徒谬论。
2.当你看到 “计算机行业人均年收入超过50万元” 的新闻是否会焦虑呢?
人均年收入的指标是不可靠的。收入低的人被薪资高的人给平均了,为平均值陷阱。在数据分析中,要看平均值指标的,把数据进行分组。
3.每一次都错过公交车的你是真的很衰吗?
墨菲定律所产生的现象,越不想发生的事情,在脑海中的印象就越深刻,会加重我们的期望,出现的概率就会越大。每天去等公交,车正常进出,正常上车的话,你对它的印象就比较浅;如果某天公交车等了一个小时都没来,你就会印象特别深刻。
统计学在生活中无处不在,给我们观察世界的一个全新的视角。
统计学的介绍
定义:统计学是通过收集、整理、分析、描述数据等手段,以达到推测所测对象的本质,甚至预测对象未来的一门综合性学科。统计学的核心是数据。
收集数据可以用爬虫,整理数据用pandas,从几百万行中整理出需要的部分,分析数据找到规律,用可视化的形式呈现出来,描述数据也可以以可视化的形式呈现。
统计学的分类
统计学不仅可以推断数据的本质,还可以做预测。
描述统计学
定义:描述统计学是指运用制表和分类,图形以及计算概括性数据来描述数据特征的各项活动。
描述数据的集中趋势,离散程度,分布形态等都是描述统计学要做的事情。
股票分析:
1.采集股票数据,对数据进行加工处理;2.计算因子值。3.概括因子的分布特征、图表展示出来,得到相关的信息。
如果用历史的数据去推断出股票的未来走势,就要用到推断性统计学。
推断统计学
定义:推断统计学是研究如何利用样本数据来推断总体特征的统计方法,是在对样本数据进行描述的基础上,对统计总体的未知数量特征做出概率形式表述的推断。包括估计、假设检验、方差分析、相关分析、回归分析等。
描述性统计学是借用现有的数据,来计算指标,衡量数据的结果,常用的均值、中位数、标准差、方差等,而推断性统计学是以样本数据来推断总体,涉及到理和函数,x轴,y轴等。
数据分析用到的比较多的是描述性统计学的知识,机器学习。机器学习、深度学习大部分用到的是描述性加推断性统计学的知识。
二者是相辅相成的,没有好坏的区别,要看你所利用数据进行的分析。
统计学的基本概念
数据
统计学研究的核心是数据。
1000(元)、“女性”、“一年级”、[2000,4000] 等均为数据,数据不仅仅是阿拉伯数据,还有分类型的数据等。
统计学数据的分类
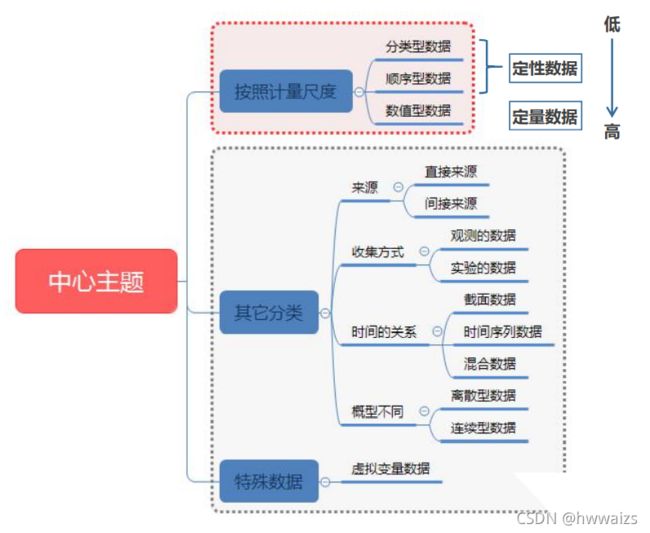
最常见的分类是分类型、顺序型、数值型数据。
分类型数据是对事物进行分类的结果,性别可以分为男和女,它们之间不能进行排序,没有先后之分的。分类型数据的特点是不能进行排序,计算。
顺序型数据,生活当中经常遇到,在饭店就餐后,APP、店员会邀请你进行评价,非常满意、满意、一般、差之间已经有了先后的顺序。顺序型数据的特点是可以进行排序,但是不能进行计算。有时可以对数据进行量化,比如非常满意为90分,满意为80分,一般为60分进行转换。
数值型数据,对数据的精确测度,比如某个人的年龄为18,体重为180斤。特点为既可以排序也可以进行计算。
分类型数据和顺序型数据也被称为定性数据,数值型数据为定量数据。数值型数据所包含的信息量最大。
脱敏:从网上下载公开的数据,但数据里又包含隐私的数据,就要对数据进行脱敏的操作。比如可以把90,80转化为非常满意、满意等等。
高级数据(数值型)可以向低级型的数据(分类型、顺序型)进行转换,使用低级数据的方法。
如“1000元”、“2500属于[2000,4000]”为数值型数据;“女性”为分类型数据;“一年级”、“[2000,4000]属于低等收入”为顺序型数据。
判断分类型和顺序型数据的指标是看数据能否进行排序。
观测的数据是没有办法人为控制的,如人的薪资,也可看到但是无法干预;
实验的数据是可以通过控制一些量来改变或者影响结果。
截面数据是指在一个时间点或者时间段内获取到的数据,有始有终的获取数据,如公司上一个月在全国的销售额等;
时间序列数据会跟着时间的变化而发生变化的数据,如股票数据的变化,跟时间是密不可分的,在不同的时间范围内呈现不同的规律;
混合数据,如2019和2020年的年薪,以及2020年和2021年的年薪数据是相互独立的。不同城市的薪资也会不同,如果用城市进行切割,获取的数据就会有局限性。可以利用维度,如不同城市不同时间的薪资,这就是混合数据。
离散型数据是独立的数据,如2018年1月1日,2021年1月1日,不可以无限细分的;
连续型数据是个范围,可以进行无限细分,如2018-1-1到2021-1-1,可以在区间内以周、月、小时等进行细分。
特殊数据,虚拟变量数据,将真实的数据转换为0,1,便于计算机使用,创建虚拟环境变量。如下表中,出现的城市为1,没有出现的为0.
| 城市 | 长沙 | 深圳 |
|---|---|---|
| 长沙 | 1 | 0 |
| 深圳 | 0 | 1 |
| 重庆 | 0 | 0 |
| 长沙 | 1 | 0 |
| 重庆 | 0 | 0 |
总体
总体是指研究对象的整个群体。如全班同学的成绩,研究对象为全班学生。与总体相关的事物,使用希腊字母表示(如:μ表示整体均值)
样本
样本是从总体中选用的一部分数据。如20岁年轻人部分人的体重。与样本相关的事物,用英文字母表示,(如:x表示样本均值),可以利用样本推算总体。
参数
研究者想要描述总体特征的概括性数字度量叫做参数,如:总体均值μ,总体标准差,总体比例等。
统计量
根据样本数据计算出来的一个量,即样本的某个特征值,如:样本均值x,样本标准差,样本比例等。不含未知参数,通过样本统计量推导出整体的参数。
变量
变量是描述事物某种特征的概念,比较大的范围,如体重。
变量值
变量值是变量的具体表现形式,简单来说也就是数据,如45KG。变量和变量值是对应的关系。
描述性统计
思考:某团APP数据库中记录了一年内60w余条消费者的消费数据,请撰写一份数据描述统计分析报告。
分析思路:
• 总体规模的描述——总量指标
• 对比关系的描述——相对指标
• 集中趋势的描述——平均指标
• 离散程度的描述——变异指标
• 分布形态的描述——偏态与峰态
• 描述性统计图表
总量指标
总量指标反映在一定时间、空间条件下某种现象的总体规模、总水平或总成果的统计指标。比如:从财务表中计算总营业额、总利润、总收入及总成本等,基本上都是求和的过程。
相对指标
相对指标是两个相互联系的指标数值之比。比如:目标完成率,指定任务实际完成的量除以目标完成量。
平均指标
集中趋势
集中趋势就是一组数据向其中心值靠拢的趋势,测度集中趋势就是寻找数据水平的代表值或中心值,反映数据整体的趋势,不同的数据类型需要不同的指标进行分析。
三十六计:
• 分类型数据可用:众数
• 顺序型数据可用:众数、分位数
• 数值型数据可用:众数、分位数、均值
众数
出现次数最多的变量值。表示符号: M o M_o Mo
问题:以下数据中,众数个数是:
1 2 3 4 5 6 没有众数
1 2 3 3 4 5 1个众数,为3
1 2 2 3 3 4 2个众数,为2,3
注意:众数并不是唯一的。
分位数
分位数是指将一个随机变量的概率分布范围分为几个等份的数值点,常用的有中位数(即二分位数)、四分位数、百分位数等。
二分位数:
• 定义:数据排序后,处于中间位置上的值。
• 表示的符号: M e M_e Me
• 计算:数据个数为n,则中位数的位置为 n + 1 2 \frac{n+1}{2} 2n+1
例题1:计算一下五个数的中位数:980,1400,1000,1200,800

注意:计算时要先进行排序。
例题2:计算一下6个数的中位数:980,1400,1000,1200,800,1650
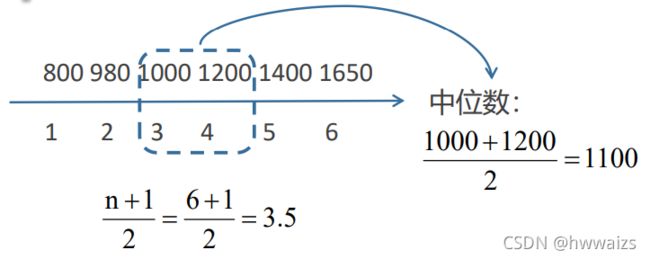
四分位数:
定义:四分位数分为下四分位数和上四分位数两种,指排序后处于25%和75%位置上的值

下四分位数: Q i Q_i Qi
• 表示符号:
• 计算: n 4 \frac{n}{4} 4n
上四分位数:
• 表示符号: Q u Q_u Qu
• 计算: 3 n 4 \frac{3n}{4} 43n
例题1:求以下数值的上四分位数和下四分位数。980 1400 1000 1200 800 1650 1100 1050 1500 950 900 1250

例题2:求以下数值的上四分位数和下四分位数。800 900 950 980 1000 1050 1100 1200 1250

算术平均数
数据的和与数据个数之比,表示的符号为: x ˉ \bar{x} xˉ
简单算术平均数(根据未分组数据计算的):
x ˉ = x 1 + x 2 + . . . + x n n = ∑ i = 1 n x i n \bar{x}=\frac{x_1+x_2+...+x_n}{n}=\frac{\sum_{i=1}^{n}{x_i}}{n} xˉ=nx1+x2+...+xn=n∑i=1nxi
加权算术平均数(根据分组数据计算的):

算术平均数容易受到异常数据的影响,下图中月均消费是1000作用,但是三月突然消费增加,得到的算术平均数就会与真实值不符。
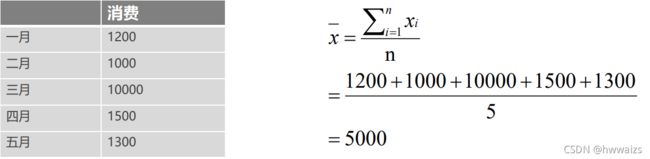
每个月的数据都是在1000左右,但是其中一个月的数值为10000,影响到整体的数据。
练习:计算一下平均消费。
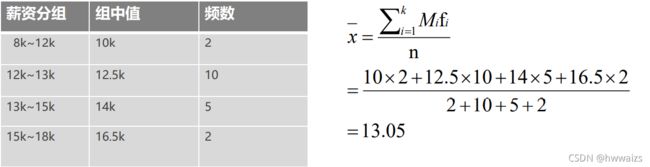
可以理解为有2个人的薪资在8k-12k之间,根据分组计算的平均值比直接计算平均数要有效一些。
局限性:
• 容易受到异常值的影响
• 适用于数字之间存在可加性(线性)的数据集上使用
以下两个图分别为公差为3的等差数列和公比为3的等比数列。左侧呈现等差数列分布,直接用算术平均数计算,可以得知当数据呈现可加性的时候,算术平均数等于中位数。右侧图表中,数据的分布是曲线的,指数级的增长,越往后数据增长越快,可以看到中位数是81,如果用算数平均数计算得到的结果为468.42,差距比较大

注意:算术平均数不适用于乘数级或者指数级增长的数据。均值跟中位数相差比较大,那么离散值就非常大,会偏差很多。
几何平均数
n个变量值乘积的n次方根
表示的符号: G G G
几何平均数(根据未分组数据计算的): G = x 1 x 2 . . . x n n G =\sqrt[n]{x_1x_2...x_n} G=nx1x2...xn
注意:
• 所有数据需大于0
• 容易受到异常值的影响
• 容易丢失有意义的尺度与单位(如,亿和元,需要先进行单位转换)

几何平均数为80.9,中位数为81,几何平均数可以解决几何级或者指数级增长数据的问题

二维图形可以将乘法的面积从218转换为66,取长补短,对应长方形的面积就变成了正方形的面积,最终面积不变;三维图形也可以取长补短,长方体的体积转变为正方体的体积,结果不变。更高维度的来说,同理可以推断。

使用算术平均数会发现A款的性能高于B款,使用几何平均数则结果相反。如果使用算术平均数,会认为聚焦200的性质比视野8对相机的影响更大,因为在计算中200占的权重更大,算术平均数并不适合计算量纲(数量级)不同的数据,需要进行标准化处理。
几何平均数把量纲(数据级)不同的数据均匀起来了(归一化),进行取长补短,会认为聚焦和视野对相机的影响是同样重要的,几何平均数比算术平均数求得的值更加精确。
使用哪一种平均数要看图形的分布,在数据分析的过程中,数据是非常多的,用肉眼可能无法看到数据是直线的形式还是弯曲的形式,这里就要求首先对数据处理进行可视化,根据数据的增长情况,如果是线性的就用算术平均数,如果是乘数或者指数级增长(数据越往后,增长速度越快,数据分布不均匀)就用几何平均数。
比如对饭店进行评价后进行平均打分,如口味66,服务0.8,环境98等数据的数量级不一致,求解的方法:1.归一化后再求平均;2.求几何平均
**应用:**适用于增长率数据的研究
1.开根号里面的值都要是大于0的,不能有负数,增长率一般都是正向的;
2.适用于处理指数级增长的问题(复利,收益率比较稳定,呈现的就是指数级的增长)
例题:股票连续4年的收益率分别为-5.0%,3.7%,26.5%,4%,计算该投资者4年的平均收益率。

使用算术平均数得到的结果为7.3%,使用几何平均数得到的结果为6.7%,数据相差将近一个点。
例题:某同学进行投资,本金为1,每年的增长率为5%,但第3年起,增长率达到了7%,求第5年年底的总金额和平均增长率。
第一年年底的金额为:1+15%=1 * (1+5%)
第二年的本金是第一年的总额:1 * (1+5%) * (1+5%)
第三年年底的金额为:1 * (1+5%) (1+5%)* (1+7%)
第五年年底的总金额为:1 * (1+5%)* (1+5%)* (1+7%)* (1+7%)* (1+7%)
用几何平均数求平均增长率:(1 * (1+5%)* (1+5%)* (1+7%)* (1+7%)* (1+7%))**(1/5)-1 -----> 开五次方根,减去本金