NLP——Seq2Seq基本原理以及Attention改进

NLP——Seq2Seq基本原理以及Attention改进

1、Seq2Seq的基本结构

1.1、Seq2Seq引入

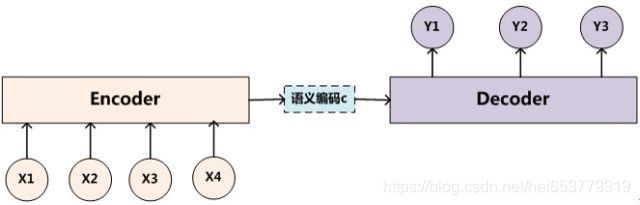
Seq2Seq本身是从机器翻译中发展过来的，他的基本思想是设计一个符合序列输入的编码器，输入一个序列数据，可以理解为一句话，句子中每个词之间是由序列关系的。然后，通过一个编码的方式，将这个序列的数据压缩到一个语义向量C中，在设计一个符合序列结构的解码器，然后通过这个解码器将这个语义向量C进行解码，生成一个新的序列数据，这个新的序列数据对应着输入数据的翻译结果。

我们举一个例子来说明一下就是，假设我们输入的是一句中文“我 爱 中国”，然后通过编码器将这句话浓缩成一个语义向量C，然后将语义向量C送入到解码器中，在通过解码器对语义向量C进行解码，最终获得翻译结构“I love China”。

1.2 Seq2Seq的结构解析

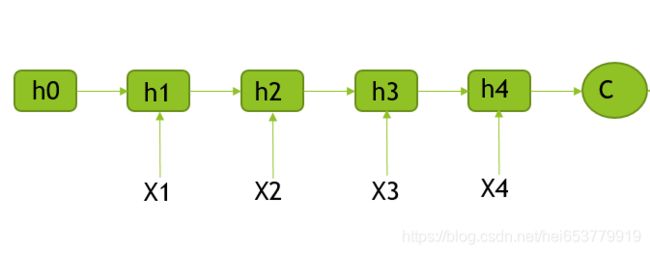
从上面的描述中，我们可以知道，Seq2Seq的本质是一种语义表现形式的转换，例如从中文表示的语义转向由英文表示的语义，在上面，我们说明了，无论是编码器的输入和是解码器的输出，都是序列数据，在神经网络中，能够处理序列数据的最为常见的模型就是循环神经网络(RNN|GRU|LSTM)。所以，在解码器和编码器，我们都选择循环神经网络作为内部结构。于是，我们便得到了整个Seq2Seq的基本结构图示：

进一步，我们将Encoder和Decoder的内部结构展示来：

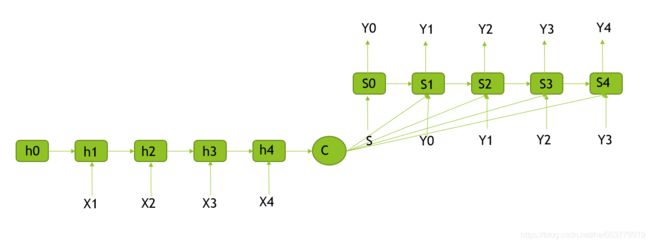
2、Seq2Seq基本流程

2.1 Seq2Seq的目标函数

我们使用$X=[X_1,X_2,X_3,...X_n]$表示输入的语句，每一个$X_i$表示一个词汇，输入的语句使用$Y=[Y_1,Y_2,...Y_n]$来表示，其中$Y_i$表示第i个时刻输出的词汇。每一个Seq2Seq模型的目标都是最大概率的去生成输出，那么也就是：
$$P(Y|X)=\prod _{i=1}^{n}P(Y_i|Y_1,Y_2,...Y_{i-1},X)$$
也就是说当前$Y_i$的输出不仅依赖于输入的句子X，还包括解码器在i时刻之前的输出，一般情况下，为了避免概率乘积的下溢，我们一般选择对概率的计算取对数。
$$P(Y|X)=\sum _{i=1}^{n}log(P(Y_i|Y_1,Y_2,...Y_{i-1},X)$$

2.2 Seq2Seq的信息的传递过程

Encoder：

1. 每一个时刻输入一个词，隐层的状态变换公式为：
   $$h_i=RNN(h_{i-1},X_i)$$
2. 读完序列的每一个词之后，会得到一个固定长度向量：
   $$C=g(V{h}_n)$$
   其中g是激活函数，V是维度变换矩阵，h_n是Encoder中最后一个隐状态。

Decoder:

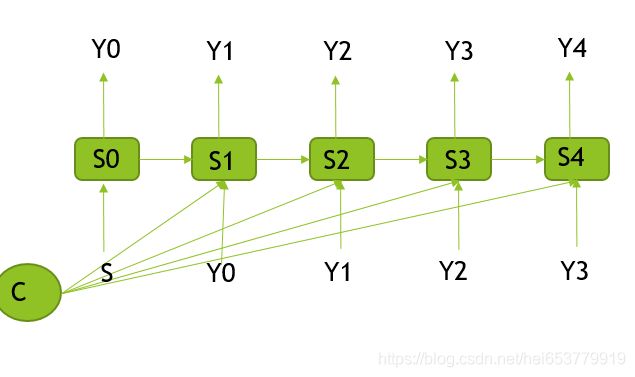
1. 有结构图可以看出，i时刻的隐状态$s_i$由前一个时刻的隐状态$s_{i-1}$，前一个时刻的输出y_{i-1}，语义向量C来作为输入，其计算公式为：
   $$s_i=RNN(s_{i-1},y_{i-1},C)$$
   其中$s_0=g(V^{\prime }C)$来决定。g表示激活函数。
2. 对于第i时刻的输出，其是由 当前时刻的隐状态$s_i$，前一个时刻的输出y_{i-1}，语义向量C来产生的，计算公式为：
   $$P=(y_i|y_{i-1},y_{i-2},y_{i-3},..y_1,C)=softmax(s_i,y_{i-1},C)$$

最终的目标函数：最大化似然函数的条件概率：
$$ma{x}_{\theta }\frac{1}{N}\sum _{i=1}^{n}log{P}_{\theta }(y_i|X)$$
其中X表示Encoder中的输入，θ表示整个模型的参数。

3、基于SoftAttention的Seq2Seq结构

3.1 Soft——Attention的引入

在引入Attention机制之前，我们先来分析一下这个模型存在的局限性。对于编码器Encoder而言，其编码的过程就是将输入X输入到一个RNN结构的循环神经网络中，按照顺序前向传播，最终获取到RNN的最后一个节点的输出作为语义向量，在将这个语义向量输入到解码器中，与解码器的前一个时刻隐状态和前一个时刻输出进行整合，最终获取到当前时刻的输出。

首先，对于每一个输出Y而言，其作为输入的语义向量是相同的，均为编码器最后的一个隐层单元。但是，这种方式是最好的吗？显然不是，我们以机器翻译作为例子，假设我们输入的英文为“I love China”，经过编码的编码之后形成语义向量C，然后输入到解码器中进行翻译的过程，最终的输出为“我 爱 中国”。我们观察一下输入和出的句子。首先对于输出“我”而言，其对应的输入是“I”，对于输出“爱”而言，其对应的输入是“love”。对于输出“中国”而言，其对应的输入是“China”。

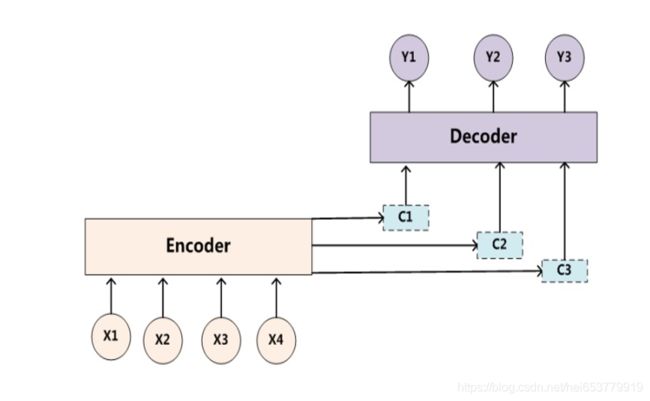
通过上面的观察，我们不难发现对于Decoder中的输出，其实是和输入是具有一定的对应性的，换句话说，每一个输出对于输入序列是具有一定的侧重性的。但是在我们上面的结构中，我们使用的均为同一个编码器的语义向量C。并没有这种侧重性的体现。为了体现这种侧重性，我们提出了Soft——Attention的结构、

在之前的结构中，由于编码器采用的是RNN的结构，根据RNN的遗忘性规律，实际上编码器更加侧重的是最后的输出单元。

3.2 Soft—Attention的计算方式

这里我们描述一下Soft—Attention的计算过程，对于Attention机制，我们可以理解为一种按照权重来对输入进行加权求和的过程。

首先，我们需要获取的就是权重，权重的计算主要分为两个部分进行，第一个部分是计算各个输入得分，第二个部分是将不同输入进行Softmax获取不同的权重值。

我们首先从得分函数score开始，得分函数的作用，其实就是衡量每一个输入和当前要输出的内容的相似度。在我们的Decoder模型中，衡量的就是当前输出的隐藏状态和各个输入的隐状态的相关性，相关性越高，说明这个输出和这个输入的相关性越高。常见的得分函数主要包括下面几种：

1. 向量点积：
   $$Score(S_t,h_j)=S^{T}H$$
2. Cosine计算相关性
   $$Score(S_t,h_j)=\frac{S^{T}H}{||S_t||\ast ||H||}$$
3. 使用MLP网络
   $$Score(S_t,h_j)=MLP(S_t,h_j)$$

我们设$Score(S_t,h_j)$的结果为$e_{tj}$，即：
$$e_{tj}=Score(S_t,h_j)$$
在获取到得分函数之后，我们下一步就是对各个输入的得分进行softmax的归一化操作生成权重：
$$a_{tj}=\frac{exp(e_{tj})}{{\sum }_{j=1}^{K}exp(e_{tj})}$$
其中K表示输入单元的个数。

当我们确定了权重之后，就是形成对应的语义向量$C_t$，其形成的过程很简单，就是根据权重对Encoder中的各个隐藏单元进行加权就和：
$$C_t=\sum _{j=1}^K{a}_{tj}{h}_j$$

然后，我们就是将语义向量和当前时刻的隐层进行合并获得最终的隐层向量：
$$S_t^{\ast }=tanh(W_C[C_t,S_t])$$

最终，我们可以确定输出为：
$$P(Y_t|X)=softmax(W_s{S}_t^{\ast })$$

以上就是在加入soft—Attention之后的计算方式。我们再来介绍一种方式，其中，在我们上面的计算的过程中，在计算相似度的时候，使用的是RNN中当前时刻的隐状态$S_t$，然后在融合语义向量之后生成新的隐状态$S_t^{\ast }$。其中$S_t$的生成是由前一个隐藏状态$S_{t-1}$和前一个时刻的输出$Y_{t-1}$决定的。另外的一种思想是在计算相似度得分的时候，使用的是前一个时刻的隐状态$S_{t-1}$，也就是：
$$e_{tj}=Score(S_{t-1},h_j)$$
$$a_{tj}=\frac{exp(e_{tj})}{{\sum }_{j=1}^{K}exp(e_{tj})}$$
$$C_t=\sum _{j=1}^K{a}_{tj}{h}_j$$

在进行输入的时候，和原始模型结构一样将前一个时刻的输出$Y_{t-1},S_{t-1}$和当前时刻的语义向量$C_t$作为解码器RNN的输入来决定RNN的输出。最后在经过softmax，获取最终概率。

介绍完上面的两种计算方式之后，我们用两张图来简单的概括一下这个过程：

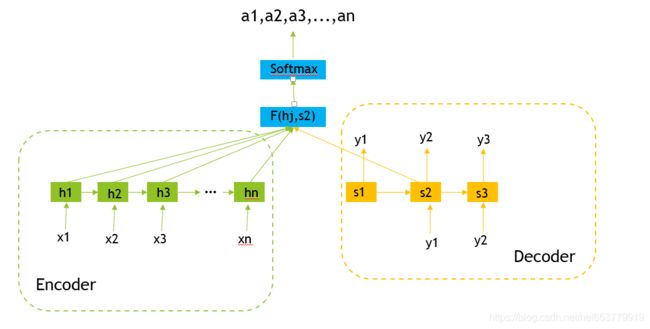
3 参考

1. 真正的完全图解Seq2Seq Attention模型