四阶龙格-库塔(Runge-Kutta)方法求解高阶微分方程(附Python代码)
用Python实现四阶龙格-库塔(Runge-Kutta)方法求解高阶微分方程
文章目录
- 用Python实现四阶龙格-库塔(Runge-Kutta)方法求解高阶微分方程
-
- 问题
- 求解步骤
问题
应用四阶龙格-库塔(Runge-Kutta)方法求解如下二阶初值问题:
{ t 2 x ′ ′ ( t ) − 2 t x ′ ( t ) + 2 x ( t ) = t 3 ln t , t ∈ [ 1 , 5 ] x ( t ) = 1 , t = 1 x ′ ( t ) = 0. t = 1 \left\{ \begin{aligned} t^2x''(t)-2tx'(t)+2x(t) & = t^3\ln t, & t\in [1,5]\\ x(t) & = 1, & t=1 \\ x'(t) & = 0. & t=1 \end{aligned} \right. ⎩⎪⎨⎪⎧t2x′′(t)−2tx′(t)+2x(t)x(t)x′(t)=t3lnt,=1,=0.t∈[1,5]t=1t=1
要求:取步长 h = 0.01 h=0.01 h=0.01,给出解 x ( t ) x(t) x(t)的图像和在 t = 0 , 0.5 , 1 , 1.5 , 2 , 2.5 , 3 , 3.5 , 4 , 4.5 , 5 t=0,0.5,1,1.5,2,2.5,3,3.5,4,4.5,5 t=0,0.5,1,1.5,2,2.5,3,3.5,4,4.5,5处的近似解.
求解步骤
-
Step1. 将原问题归结为其等价问题
引进新的变量 y ( t ) = x ′ ( t ) y(t)=x'(t) y(t)=x′(t)将高阶微分方程的初值问题归结为如下一阶微分方程组的初值问题来求解.
{ x ′ ( t ) = y , t ∈ [ 1 , 5 ] y ′ ( t ) = t 3 ln t + 2 t y − 2 x t 2 , t ∈ [ 1 , 5 ] x ( t ) = y , t = 1 y ( t ) = 0. t = 1 \left\{ \begin{aligned} x'(t) & = y, & t\in [1,5]\\ y'(t) & = \frac{t^3\ln t +2ty -2x}{t^2}, & t\in [1,5]\\ x(t) & = y, & t=1\\ y(t) & = 0. & t=1 \end{aligned} \right. ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧x′(t)y′(t)x(t)y(t)=y,=t2t3lnt+2ty−2x,=y,=0.t∈[1,5]t∈[1,5]t=1t=1 -
Step2. 四阶龙格-库塔方法的离散格式
针对以上一阶微分方程组的初值问题应用四阶龙格-库塔方法构造得到以下离散格式:
{ x n + 1 = x n + h 6 ( K 1 + 2 K 2 + 2 K 3 + K 4 ) , y n + 1 = y n + h 6 ( L 1 + 2 L 2 + 2 L 3 + L 4 ) . \left\{ \begin{aligned} x_{n+1} & = x_n +\frac{h}{6}(K_1 + 2K_2 + 2K_3 + K_4),\\ y_{n+1} & = y_n +\frac{h}{6}(L_1 + 2L_2 + 2L_3 + L_4). \end{aligned} \right. ⎩⎪⎪⎨⎪⎪⎧xn+1yn+1=xn+6h(K1+2K2+2K3+K4),=yn+6h(L1+2L2+2L3+L4).
其中
{ K 1 = f ( t n , x n , y n ) , K 2 = f ( t n + h 2 , x n + h 2 K 1 , y n + h 2 L 1 ) , K 3 = f ( t n + h 2 , x n + h 2 K 2 , y n + h 2 L 2 ) , K 4 = f ( t n + h , x n + h K 3 , y n + h L 3 ) , L 1 = g ( t n , x n , y n ) , L 2 = g ( t n + h 2 , x n + h 2 K 1 , y n + h 2 L 1 ) , L 3 = g ( t n + h 2 , x n + h 2 K 2 , y n + h 2 L 2 ) , L 4 = f ( t n + h , x n + h K 3 , y n + h L 3 ) . \left\{ \begin{aligned} K_1 & = f(t_n,x_n,y_n),\\ K_2 & = f(t_n + \frac{h}{2},x_n + \frac{h}{2}K_1,y_n + \frac{h}{2}L_1),\\ K_3 & = f(t_n + \frac{h}{2},x_n + \frac{h}{2}K_2,y_n + \frac{h}{2}L_2),\\ K_4 & = f(t_n + h,x_n + hK_3,y_n + hL_3),\\ L_1 & = g(t_n,x_n,y_n),\\ L_2 & = g(t_n + \frac{h}{2},x_n + \frac{h}{2}K_1,y_n + \frac{h}{2}L_1),\\ L_3 & = g(t_n + \frac{h}{2},x_n + \frac{h}{2}K_2,y_n + \frac{h}{2}L_2),\\ L_4 & = f(t_n + h,x_n + hK_3,y_n + hL_3). \end{aligned} \right. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧K1K2K3K4L1L2L3L4=f(tn,xn,yn),=f(tn+2h,xn+2hK1,yn+2hL1),=f(tn+2h,xn+2hK2,yn+2hL2),=f(tn+h,xn+hK3,yn+hL3),=g(tn,xn,yn),=g(tn+2h,xn+2hK1,yn+2hL1),=g(tn+2h,xn+2hK2,yn+2hL2),=f(tn+h,xn+hK3,yn+hL3).
这是一步法,利用节点 t n t_n tn上的值 x n , y n x_n,y_n xn,yn,由上 式顺序计算 K 1 , L 1 , K 2 , L 2 , K 3 , L 3 , K 4 , L 4 K_1,L_1,K_2,L_2,K_3,L_3,K_4,L_4 K1,L1,K2,L2,K3,L3,K4,L4,然后代入离散格式即可求得节点 t n + 1 t_{n+1} tn+1上的 x n + 1 , y n + 1 x_{n+1},y_{n+1} xn+1,yn+1. -
Step3. 利用龙格-库塔法求解高阶微分方程的
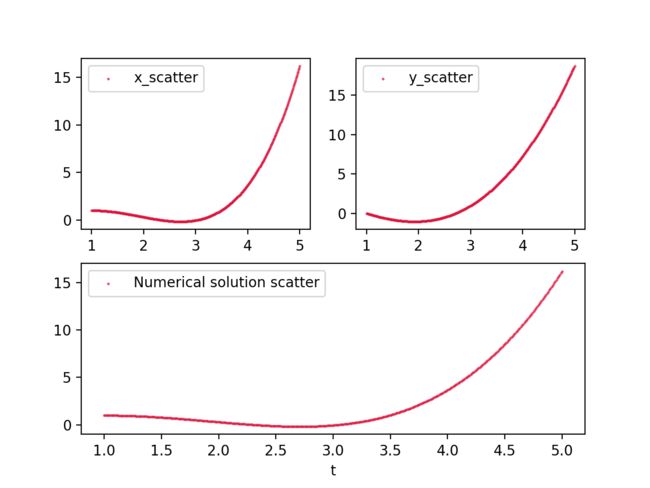
Python代码如下:# 开发者: Leo 刘 # 开发环境: macOs Big Sur # 开发时间: 2021/9/28 4:31 下午 # 邮箱 : [email protected] # @Software: PyCharm # ---------------------------------------------------------------------------------------------------------- import math import matplotlib.pyplot as plt def f(t, x, y): a = y return a def g(t, x, y): a = (t ** 3 * math.log(t) + 2 * t * y - 2 * x) / t ** 2 return a def RK4(t, x, y, h): """ :param t: t 的初始值 :param x: x 的初始值 :param y: y 的初始值 :param h: 时间步长 :return: 迭代新解 """ tarray, xarray, yarray = [], [], [] while t <= 5: tarray.append(t) xarray.append(x) yarray.append(y) t += h K_1 = f(t, x, y) L_1 = g(t, x, y) K_2 = f(t + h / 2, x + h / 2 * K_1, y + h / 2 * L_1) L_2 = g(t + h / 2, x + h / 2 * K_1, y + h / 2 * L_1) K_3 = f(t + h / 2, x + h / 2 * K_2, y + h / 2 * L_2) L_3 = g(t + h / 2, x + h / 2 * K_2, y + h / 2 * L_2) K_4 = f(t + h, x + h * K_3, y + h * L_3) L_4 = g(t + h, x + h * K_3, y + h * L_3) x = x + (K_1 + 2 * K_2 + 2 * K_3 + K_4) * h / 6 y = y + (L_1 + 2 * L_2 + 2 * L_3 + L_4) * h / 6 return tarray, xarray, yarray def main(): tarray, xarray, yarray = RK4(1, 1, 0, 0.01) print("龙格-库塔 数值结果".center(168)) print('-' * 178) print("对象\\时刻\t", "t=0\t\t", " t=0.5\t\t", " t=1\t\t\t", " t=1.5\t\t", " t=2\t\t\t", " t=2.5\t\t\t", " t=3\t\t\t", " t=3.5\t\t", " t=4\t\t\t", " t=4.5\t\t\t", " t=5") print('-' * 178) print("x:", end='') for i in range(len(xarray)): if i % 40 == 0: print("\t\t", "%8.4f" % xarray[i], end='') print('\n', '-' * 177) print("y:", end='') for i in range(len(yarray)): if i % 40 == 0: print("\t\t", "%8.4f" % yarray[i], end='') print('\n', '-' * 177) plt.figure('龙格-库塔 数值结果') plt.subplot(221) # plt.plot(tarray, xarray, label='x_runge_kutta') plt.scatter(tarray, xarray, label='x_scatter', s=1, c='#DC143C', alpha=0.6) # plt.xlabel('t') plt.legend() plt.subplot(222) # plt.plot(tarray, yarray, label='y_runge_kutta') plt.scatter(tarray, yarray, label='y_scatter', s=1, c='#DC143C', alpha=0.6) # plt.xlabel('t') plt.legend() plt.subplot(212) # plt.plot(tarray, xarray, label='runge_kutta') plt.scatter(tarray, xarray, label='Numerical solution scatter', s=1, c='#DC143C', alpha=0.6) plt.xlabel('t') plt.legend() plt.show() if __name__ == "__main__": main()- Step4. 代码的运行结果如下:
龙格-库塔 数值结果 ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 对象\时刻 t=0 t=0.5 t=1 t=1.5 t=2 t=2.5 t=3 t=3.5 t=4 t=4.5 t=5 ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- x: 1.0000 0.8579 0.5080 0.1042 -0.1564 -0.0416 0.7105 2.3875 5.2995 9.7769 16.1685 --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- y: 0.0000 -0.6689 -1.0161 -0.9205 -0.2855 0.9689 2.9116 5.6026 9.0952 13.4374 18.6728 ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
问题来源: 《微分方程数值解》–M.Ran