【数据挖掘】6. 核函数

• 目前为止我们还没有考虑不可分的数据集

  本节目的：使用核函数（将数据集映射到另一个更高维的空间）来解决不可分的数据集，来保证线性可分性

• 动机

  • 某些线性不可分的数据集，可以用圆形来划分
  • 在二维平面内不可分的数据集，扩展到三维后可以划分

• 提高维度可以保证线性可分性

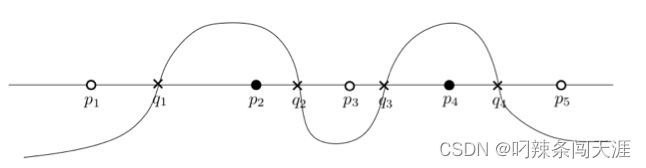
  • 对于一维空间的一系列点，如图中 $p_1,p_2,p_3,p_4,p_5$ （此时先考虑点的数量是奇数），总能在二维空间找到一条曲线，将其根据标签划分开

    

  • 通过在每对不同标签的点之间随机选择一个点 $q$ ，定义一个多项式函数：
    $$f(x)=-(x-q_1)(x-q_2)(x-q_3)(x-q_4)$$
    如下图，对于空心点，其函数值都小于 0，对于实心点，其函数值都大于 0

    

  • $f(x)$ 可以展开成如下形式：
    $$f(x)=c_0+c_{1}x+c_2{x}^2+\cdots +c_{n-1}{x}^{n-1}$$
    所以，如果将每一个点 $x\in P$ 转换成 $n$ 维空间上的点 $(1,x,x^2,\dots ,x^{n-1})$ ，那么其一定可以被 $n$ 维空间中过原点的一个平面划分

• 提高维度解决可分性带来的效率问题

  • 当转换的维度过高时，每一个点的维度转换计算消耗都会很高
  • 核函数就是解决这个问题

• 核函数

  一个核函数 $K$ 是从 ${\mathbb{R}}^d\times {\mathbb{R}}^d$ 到 $\mathbb{R}$ 的一个函数，它存在以下属性：

  存在一个映射 $\varphi :{\mathbb{R}}^d\to {\mathbb{R}}^{d^{\prime }}$ ， 使得对于任意两个给定的点 $p,q\in {\mathbb{R}}^d$ ，$K(\mathbf{p},\mathbf{q})$ 等于 $\varphi (p)$ 和 $\varphi (q)$ 的点乘， ${\mathbb{R}}^{d^{\prime }}$ 被称作核空间

  • 多项式核
    $$K(\mathbf{p},\mathbf{q})=(\mathbf{p}\cdot \mathbf{q}+1{)}^c$$
    $c$ 是大于等于 1 的整数

    • 示例

      考虑 $d=2$ ，$c=2$ ，$K(p,q)$ 就可以展开成如下形式：
      $$\begin{array}{rl}K(\mathbf{p},\mathbf{q})=& (\mathbf{p}\cdot \mathbf{q}+1{)}^2=(p[1]q[1]+p[2]q[2]+1{)}^2\\ =& 1+(p[1]{)}^2(q[1]{)}^2+(p[2]{)}^2(q[2]{)}^2+\\ & 2(p[1]p[2])(q[1]q[2])+2p[1]q[1]+2p[2]q[2]\end{array}$$

      按照向量点乘的形式从 $K(\mathbf{p},\mathbf{q})$ 中拆分出两个向量，两个向量都会有如下的映射关系：
      $$\varphi (p)=\left(1,p[1{]}^2,p[2{]}^2,\sqrt{2}p[1]p[2],\sqrt{2}p[1],\sqrt{2}p[2]\right)$$
      核空间的维度为 $C_4^2=6$

  • 高斯核
    $$K(\mathbf{p},\mathbf{q})=\exp \left(-\frac{\mathrm{dist}(\mathbf{p},\mathbf{q}{)}^2}{2{\sigma }^2}\right)$$

    • $\sigma >0$ 称作带宽，$\mathrm{dist}(\mathbf{p},\mathbf{q})$ 是 $p,q$ 之间的欧氏距离，高斯核将 $d$ 维空间的点映射到了无限维的空间
    • 当 $d=1$ 时，根据 $e$ 的泰勒展开式，高斯核的展开形式如下：

    $$\begin{array}{rl}& \exp \left(-\frac{\mathrm{dist}(p,q{)}^2}{2{\sigma }^2}\right)=\exp \left(-\frac{p^2-2pq+q^2}{2{\sigma }^2}\right)=\\ & \exp \left(-\frac{p^2+q^2}{2{\sigma }^2}\right)\exp \left(\frac{pq}{{\sigma }^2}\right)=\frac{1}{e^{\frac{p^2}{2{\sigma }^2}}}\frac{1}{e^{\frac{q^2}{2{\sigma }^2}}}\exp \left(\frac{pq}{{\sigma }^2}\right)\\ & =\frac{1}{e^{\frac{p^2}{2{\sigma }^2}}}\frac{1}{e^{\frac{q^2}{2{\sigma }^2}}}\left(1+\frac{pq}{{\sigma }^2}+\frac{(p/\sigma {)}^2(q/\sigma {)}^2}{2!}+\frac{(p/\sigma {)}^3(q/\sigma {)}^3}{3!}+\dots \right)\end{array}$$

    • 所以可以得到如下映射关系：
      $$\varphi (p)=\left(\frac{1}{e^{\frac{p^2}{2{\sigma }^2}}},\frac{p/\sigma }{e^{\frac{p^2}{2{\sigma }^2}}},\frac{(p/\sigma {)}^2}{\sqrt{2!}\cdot e^{\frac{p^2}{2{\sigma }^2}}},\frac{(p/\sigma {)}^3}{\sqrt{3!}\cdot e^{\frac{p^2}{2{\sigma }^2}}},\dots \right)$$

    • 定理：对于任意 $\sigma$ ，高斯核都能划分有线数量的点集合

• 在转换后的空间内寻找划分平面

  我们不想在转换后的核空间内重新具体的考虑映射关系 $\varphi$ 中的具体内容（在多项式核中维度过高，在高斯核中维度无限，不可能实现），使用感知器（Perceptron）可以不在核空间内运算

  • 在感知器中：

    如果 violation point $p$ 存在，对 $\mathbf{w}$ 进行如下优化：

    • 如果 p 的标签是 $1$ ，那么 $\mathbf{w}\leftarrow \mathbf{w}+p$
    • 如果 p 的标签是 $-1$ ，那么 $\mathbf{w}\leftarrow \mathbf{w}-p$

  • 在核空间 ${\mathbb{R}}^{d^{\prime }}$ 中，感知器的形式变为：

    如果 violation point $\varphi (p)$ 存在，对 $\mathbf{w}$ 进行如下优化：

    • 如果 $\varphi (p)$ 的标签是 $1$ ，那么 $\mathbf{w}\leftarrow \mathbf{w}+\varphi (p)$
    • 如果 $\varphi (p)$ 的标签是 $-1$ ，那么 $\mathbf{w}\leftarrow \mathbf{w}-\varphi (p)$

  • 对于 violation point $p\in P$ ，$p$ 被用来调整 $\mathbf{w}$ 的次数记作 $t_p$ ，$P_1$ 是 $P$ 中标签为 $1$ 的点，$P_{-1}$ 是 $P$ 中标签为 $-1$ 的点,那么经过调整后的 $\mathbf{w}$ 可以表示为：
    $$\mathbf{w}=\sum _{p\in P_1}{t}_p\varphi (p)-\sum _{p\in P_{-1}}{t}_p\varphi (p)$$

  • 如果我们给上边的公式左右两边同时点乘任意一个在核空间的点 $\varphi (q)$，可以得到：
    $$\begin{array}{rl}\mathbf{w}\cdot \varphi (q)& =\left(\sum _{p\in P_1}{t}_p\varphi (p)-\sum _{p\in P_{-1}}{t}_p\varphi (p)\right)\varphi (q)\\ & =\left(\sum _{p\in P_1}{t}_p(\varphi (p)\cdot \varphi (q))\right)-\left(\sum _{p\in P_{-1}}{t}_p(\varphi (p)\cdot \varphi (q))\right)\\ & =\sum _{p\in P_1}{t}_p\cdot K(p,q)-\sum _{p\in P_{-1}}{t}_p\cdot K(p,q)\end{array}$$

  • 因此，只要对每一个 violation point 维护一个 $t_p$ ，我们就不需要在核空间内计算点乘

• 如何在核空间中的点集合上应用基于Margin的泛化定理？

• 如何证明定理：对于任意 $\sigma$ ，高斯核都能划分有线数量的点集合？