几个常用机器学习算法 - 逻辑回归

作者：xg123321123

出处：http://blog.csdn.net/xg123321123/article/details/53011358

声明：版权所有，转载请联系作者并注明出处

1 回归

在数学上来说,回归是给定一个点集，然后用一条曲线去拟合。
如果这条曲线是一条直线，那就被称为线性回归；如果是一条二次曲线，就被称为二次回归。
回归还有很多的变种，如locally weighted回归，logistic回归等等。

一个简单的例子：如果想评估一个房屋的价值，那么需要考虑很多因素，比如面积、房间数量、地段、朝向等等（这些影响房屋价值的因素被称为特征），此处，为了简单，我们假设只考虑一个因素的影响，面积。

假设以往房屋销售的数据如下：

面积(m^2) 销售价钱（万元）

123 250

150 320

87 160

102 220

… …

为了直观，可以画一个图，x轴是房屋的面积。y轴是房屋的售价，如下：

如果有个新户型，在以往的销售记录中是没有的，那么就需要进行重新评估了。

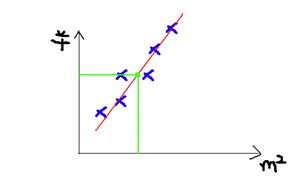
我们先用一条曲线去尽量拟合以往的数据，然后再根据新的户型数据，找到曲线上对应的价格。
当用直线去拟合时，大概是这样：

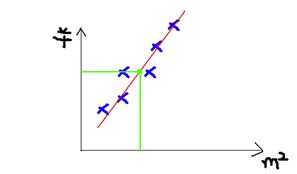
图中绿色的点，就是我们用来预测的点。
上例中特征是两维的，结果是一维的。
回归能够解决特征多维，结果是一维多离散值或一维连续值的问题。

2 线性回归

线性回归假设特征和结果满足线性关系。
线性关系的表达能力很强，每个特征对结果的影响强弱可以由前面的参数体现，而且每个特征变量可以先映射到一个函数，然后再参与线性计算。这样就可以表达特征与结果之间的非线性关系。

我们用 X1 ， X2 .. Xn 描述特征的分量，比如 x1 =房间的面积， x2 =房间的朝向等等.
接着我们以这些特征来构建一个线性的估计函数：

h(x)=hθ(x)=θ0+θ1x1+...θnxn

θ 称为参数，用来调整每个特征的影响力，比如到底是房屋的面积更重要还是房屋的地段更重要。
我们令X0 = 1，然后用向量的方式来表示上面的等式：

hθ(x)=θT(X)

同时，也需要一个损失函数来评估选取的参数 θ 是否足够好：

J(θ)=12∑i=1m(hθ(x(i))−y(i))2

最后就是采取一些优化方法来取得 θ ，使损失函数取值最小。

3 逻辑回归

一般来说，回归不用在分类问题上，因为回归是连续型模型，且受噪声影响比较大。
如果硬要用来分类，可以使用logistic回归。

这里有一篇博客帮助理清逻辑回归的思路。

3.1 逻辑分布

连续随机变量X服从逻辑分布，是指 X 具有下列分布函数和密度函数，概率密度函数是分布函数求导得来。

F(x)=P(X⩽x)=11+e−(x−μ)/s

f(x)=F'(x)=e−(x−μ)/sγ(1+e−(x−μ)/s)2

这里μ是位置参数，而s 是形状参数。
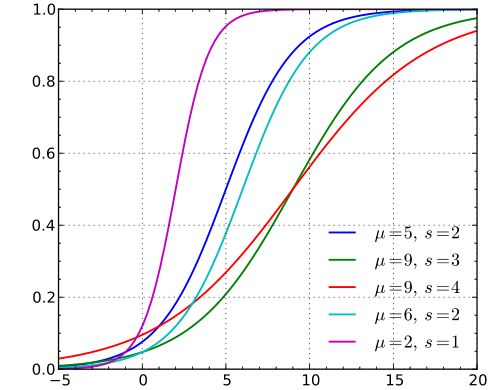
逻辑分布在不同的 μ 和s 的情况下，其概率密度函数 f(x;μ,s) 的图形如下。

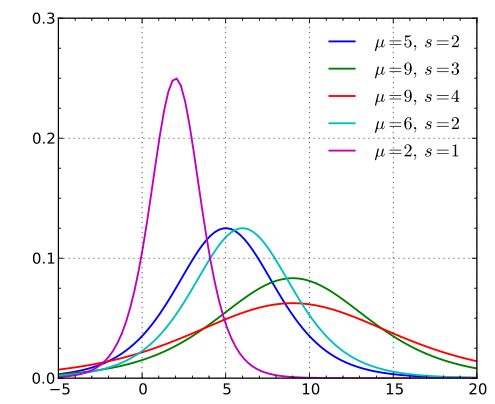
逻辑斯蒂分布在不同的 μ 和s的情况下，其概率分布函数 F(x;μ,s) 的图形如下。

可以看到，逻辑分布和高斯分布的密度函数差不多。
特别注意逻辑分布的概率分布函数自中心附近增长速度较快，而在两端的增长速度相对较慢。
形状参数s的数值越小，则概率分布函数在中心附近增长越快。

当 μ=0 , s=1 时，逻辑分布的概率分布函数就是我们常说的sigmoid函数：

σ(a)=11+e−a

导数为：

dσda=σ(1−σ)

3.2 逻辑回归

逻辑回归用来解决分类问题。
根据一些已知的训练集训练好模型，再对新的数据进行预测属于哪个类。

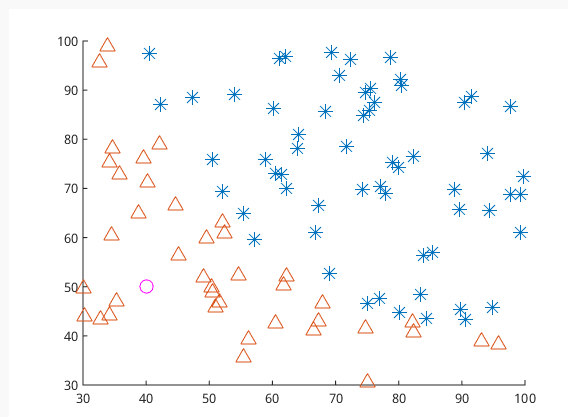
上图有一些属于两个类的数据，逻辑回归的目标是找到一个有足够好区分度的决策边界，将两类很好的分开。

假设已经存在这样一个边界，针对于图中线性可分的情况，这条边界是
输入特征向量的线性组合，假设输入的特征向量为 x∈Rn (图中输入向量为二维)， Y 取值为0，1。那么决策边界可以表示为w1x1+w2x2+b=0.

假如存在一个例子使得 hw(x)=w1x1+w2x2+b>0 ，那么可以判断它类别为1，这个过程通过决策函数的符号来判断属于哪一类,实际上是感知机。
而逻辑回归需要再进一步，它要找到分类概率 P(Y=1) 与输入向量 x 的直接关系，然后通过比较概率值来判断类别。

逻辑回归本质上其实是线性回归，但是在特征到结果的映射中加入了一层函数映射，即先把特征进行线性求和，然后使用函数g(z)作为假设函数来预测，将连续值映射到0和1上。

g(z) 是当μ=0,s=1时的逻辑分布的概率分布函数：sigmoid函数。

逻辑回归的假设函数如下，假设线性回归函数是 θTX ，而 g(z)=11+e−z ，那么可得

hθ(x)=g(θTX)=11+e−θTX

逻辑回归用来预测结果属于0或者1的二值分类问题。
这里假设二值满足伯努利分布，也就是

P(y=1|x;θ)=hθ(x)

P(y=0|x;θ)=1−hθ(x)

然后用极大似然估计求得最优参数。

3.3 多项逻辑回归

上面的逻辑回归是二项分类模型，可以将其推广为多项逻辑回归，用于多类分类。

P(Y=k|x;θ)=e−θTX1+∑K−1k=1e−θTX,k=1,2...,K−1

P(Y=K|x;θ)=11+∑K−1k=1e−θTX

其中，二项逻辑回归的参数估计法也能用在多项逻辑回归中。

---

本博客参考自
《对线性回归，logistic回归和一般回归的认识》
《浅析Logistic Regression 》
《Logistic Regression 模型简介》
《逻辑斯蒂回归（Logistic Regression） 》
《统计学习方法 李航》