class2 Nearest Neighbors 最近邻搜索

class2 Nearest Neighbors

最近邻搜索问题

Nearest Neighbor (NN) Problem

主要有两种NN问题

• K-NN

  在空间M中有一个点集S,一个查询点$q\in M$,找到查询点在S中最近的k个点

  下图是3-NN

  

• Fixed Radius-NN

  在空间M中有一个点集S,一个查询点$q\in M$,找到所有在S中和查询点距离小于r的点

  $||s-q||<r$
  

• NN 问题的应用领域

  • 表面法向量估计
  • 噪点滤除
  • 降采样
  • 聚类
  • 特征点检测和特征提取
  • 深度学习
  • …

• 为什么最近邻搜索对点云来说很困难?

  • 对于图像,最近邻搜索只要简单的$x+\Delta x,y+\Delta y$
  • 对于点云来说
    • 点云不规则
    • 比图像多一个维度
    • 点云数据量巨大

• Core Ideas Shared by BST, kd-tree, octree

  • 空间分割

    • 把空间分割成不同的区域
    • 只在一些特定的区域内搜索,不是搜索所有的数据

  • 提前停止搜索

1.Binary Search Tree

二叉搜索树

• 节点定义

  struct Node() 
  {
      Node* left;
      Node* right;
      int val;// 存储的属性
      int key;// 节点的数值
      Node(int val,int key):key(key),value(value);
  };
  

• 建树/插入元素

  vector<int> db_data(db_size);
  
  Node* insert(Node* root,int key,int value) {
      //
      if(root==nullptrt) {
          root = new Node(key,value);
      } else if(key > root->key) {
          root = insert(root->right,key,value);
      } else if(key < root->key) {
          root = insert(root->left,key,value);
      } else {
          printf("key already exits\n");
      }
      return root;
  }
  
  Node* root = new root();
  for(int i=0;i<db_size;++i) {
      root = insert(root,db_data[i],i);
  }
  

• 插入复杂度

  O(h),h是树的深度

  最坏的情况,h就是BST元素的个数,即称为了一个链表,$h=n$

  最好的情况,平衡二叉树,$h=lo{g}_2(n)$

• 查找一个元素

  给定一个二叉搜索树BST,和一个查询数据query(key),在这棵树中查询等于key的节点,如果没有返回null

  有递归和迭代两种查找方法

  • 递归

    Node* search_recursive(Node* root,int key) {
        if(root == nullptr || root->key == key) {
            return root;
        }
        if(key > root->key) {
            return root = search(root->right,key);
        } else {
            return root = search(root->left,key);
        }
    }
    

  • 迭代

    Node* search_recursive(Node* root,int key) {
        Node* current_node = root;
        while(!current_node) {
            if(current_node->key == key) {
                break;
            } else if(current_node->key > key) {
                current_node = current_node->left;
            } else {
                current_node = current_node->right;
            }
        }
        return current_node;
    }
    

  • 两种查询方式的对比
    
    在GPU上面选择循环

• BST-1NN search
  

查询数据-query point 11

查询过程,使用一个变量worst distance,表示目前二叉树到查询点最近的距离,就是应该查询的最远距离,超过这个距离的数据就不需要查询了;

Worst distance is the largest distance that you should search around the query point

1. 首先第一个节点是8

​ a) worst distance = 3 (11-8)

​ 就算不向下查找,也知道这棵树离查询点的距离至少是3

​ b) 在节点8左边的节点值都比8小,所以距离查询点的距离一定比3大,所以不需要查询节点8的左节点

​ c) 节点8的右子树数值范围(8,+inf),worst distance = 3,还可以更小,需要 查询的范围(8,14) 在右子树里面

​ 下一次查询的范围是(当前节点值,查询数据+worst distance)

2. 来到查询的第二个节点10

​ a) worst distance = 1(11-10)

​ b) 同第一个节点,只需要查询节点10的右子树(10,+inf),查询范围是(10,12)在右子树里面

3. 查询第三个节点 14

​ a) worst distance = 1

​ 此时的距离=14-11=3>1,所以worst_distance还是1

​ b) 14比查询点大,14的左子树数值范围(10,14),查询范围是(10,12),在左子树里面,所以需要查询左子树

4. 查询第四个节点13,同第3)步,继续查它的左子树,左子树为空,返回到节点14

​ 需要查询14的右子树吗?右子树范围是(14,+inf),需要查询的范围是(10,12),不需要

5. 返回节点10

​ 需要查询10的左子树吗?左子树范围是(8,10),需要查询的范围是(10,12),不需要

6. 返回节点8

​ 需要查询8的左子树吗?左子树范围是(-inf,8),需要查询的范围是(10,12),不需要

上面查询的过程就是NN搜索的核心,跳过了很多不需要查询的区域

如下图所示,随着worst distance的减小,就不需要查询右子树的内容了

• BST-kNN search
  二叉搜索树的kNN搜索
  

  • Worst Distance for kNN

    建立一个容器存储距离结果,容器降序排序,最后一个就是worst_distance

    如果当前距离

• Radius NN Search

  与kNN类似,不过worst_disttance固定为指定的radius,只要dist

2.Kd Tree

BST只适用于一维数据的最近邻查找

高维数据:使用Kd树

• 是BST在高维上的扩展

  • 在高维的每一个维度进行一个BST

• Kd-tree建树

  • 如果只有一个点,或者 number of points < leaf_size,就建立一个叶子节点
  • 否则,在选择的轴上面,使用一个超平面把数据分成两半
  • 重复上面两步,直到没有数据可分,全部都是叶子节点

• 以二维数据为例
  
  有两种在维度上划分的方法,一种是超平面选择在数据点上面,另一种不是在数据点上,只是习惯的问题,课程中使用第二种划分方法,每一个数据点都在一个区域里面,点要么在左边,要么在右边,不会在中间;

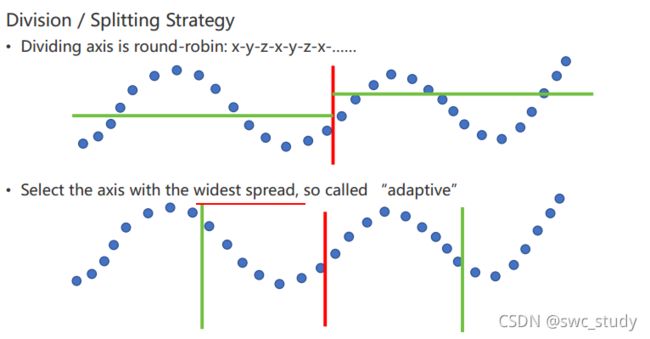
  • 切割策略

    寻找到要切割的维度

    • 每一个维度轮流切

    • 自适应切,找到方差最大的方向去切

    • 这两种切割方法对最后的NN结果影响不大,所以选择第一种简单一点

  • 建树过程
    
    最小点数设置为1，即叶子节点保存最多一个数据点

    首先在x轴上面切,使用s1这个超平面,然后在左边区域,在y轴上面用s2切割
    
    依次类推

  • kd tree节点的表达

    class KDTreeNode
    {
    public:
        KDTreeNode();
        ~KDTreeNode();
    
    private:
        // int dim;		// 节点的维度
        
        int cut_dim;    // dimension to cut;
        
        float cut_val;  //cut value 切割面的位置(默认-1)
    
        vector<int> point_indices; // 存储当前节点中数据的下标
    
        KDTreeNode *left, *right;  // pointers to left and right nodes.
        // 是否为叶子节点
        inline bool is_leaf() {
            if(cut_value == -1) {
                return true;
            }
            return false;
        }
    };
    

    
    ​ 左下角这个节点:

    ​ cut_dim = y

    ​ cut_val = s2

    ​ points=[a,b,d,e]

    右上角这个节点:

    ​ cut_dim = y

    ​ cut_val = -1

    ​ points=[i]

  • 建树

    选择一个维度,切割两半,再递归的进行左右两边的划分

  

  • 时间复杂度

    n个数据点,分为logn层,排序是nlogn,所以整体时间复杂度是O(n log n log n)

    可以把排序算法替换为找中值算法O(n) 所以整体时间复杂度是O(n log n)

    在实际建树过程中,会使用一些技巧降低时间复杂度

    1. 选择一个节点中的一部分数据进行排序,选择切割位置,而不对全部数据进行排序

    2. 使用均值代替中值,选取切割位置

    这样不会保证是平衡的kd-tree,但是基本上可以用,而且建树速度很快

  • kNN Search

    也需要一个变量worst distance

    

    需不需要查找蓝色区域:

    1. 如果查询点在蓝色区域内部,需要查询,worst distance可能为0

       或者

    2. q到当前节点分割面的位置距离小于worst distance,也需要查询,因为有可能蓝色区域内存在距离查询点更近的点

    

  • Radius-NN Search
    建树&NN search 伪代码

Node-data就相当于二叉搜索树节点的值,来了一个数据,对应维度的数值就和它相比,比它小是左孩子,比它大是右孩子

range:数据点集?

从上面对k-d树节点的数据类型的描述可以看出构建k-d树是一个逐级展开的递归过程。下表给出的是构建k-d树的伪代码:

k-d树查询算法的伪代码:


上述两次实例表明，当查询点的邻域与分割超平面两侧空间交割时，需要查找另一侧子空间，导致检索过程复杂，效率下降。研究表明N个节点的K维k-d树搜索过程时间复杂度为：
$t_{worst}=O(k{N}^{1-1/k})$。

以上为了介绍方便，讨论的是二维情形。像实际的应用中，如SIFT特征矢量128维，SURF特征矢量64维，维度都比较大，直接利用k-d树快速检索（维数不超过20）的性能急剧下降。假设数据集的维数为D，一般来说要求数据的规模N满足N»2D，才能达到高效的搜索。所以这就引出了一系列对k-d树算法的改进。有待进一步研究学习。