AI学习笔记（七）图像滤波器、OpenCV算法解析

图像滤波器

图像噪声

噪声的产生

• 图像噪声是图像在获取或是传输过程中受到随机信号干扰，妨碍人们对图像理解即分析处理的信号。
• 很多时候将图像噪声看做多为随机过程，因而描述噪声的方法完全可以借用随机过程的描述，也就是使用随机过程的描述，也就是用它的高斯分布1函数和概率密度分布函数。
• 图像噪声的产生来自于图像获取中的环境条件和传感器元器件自身的质量，图像在出阿叔过程中产生图像噪声的主要原因是所用的传输信道收到了噪声了污染。

信噪比

在噪声的概念中，通常采用**信噪比（Signal-Noise Rate， SNR)**衡量图像噪声。通俗地姜就是信号占多少，噪声占多少，SNR越小，噪声占比越大。
在信号系统中，计量单位为dB，为$10lg(PS/PN)$，$PS$与$PN$分别代表信号和噪声的有效功率。
在这里，采用信号像素点的占比充当SNR，以衡量所添加噪声的多少。
举个例子，假设一张图像的高维10，宽为10，共计100个像素点，想让其中20个像素点变为噪声，其余80个像素点保留原值，则这里定义的$SNR=80/100=0.8$。

高斯噪声

• 高斯噪声（Gaussian noise）是指它的概率密度函数从高斯分布的一类噪声。
• 特别地，如果一个噪声，它的幅度分布服从高斯分布，而他的功率谱密度又是均匀分布的，则称它为高斯白噪声。
• 必须区分高斯噪声和白噪声两个不同的概念。高斯噪声是指噪声的概率密度函数服从高斯分布，白噪声是指噪声任意两个采样样本之间不想管，两者描述的角度不同，白噪声不必服从高斯分布，高斯分布的噪声不一定是白噪声。
  产生的原因：
  1）图像传感器在拍摄的时候不够明亮、亮度不够均匀
  2）电路各元器件自身噪声相互影响
  3）图像传感器长期工作，温度过高
  一个正常的高斯分布公式$G(d)$，得到的像素$Pout$
  $$Pout=Pin+XMeans+\sigma G(d)$$其中$d$为一个线性的随机数，$G(d)$是随机数的高斯分布随机值。
  给一幅图像加上高斯噪声的处理顺序如下：
  1）输入参数$\sigma$和$XMeans$
  2）以系统时间为种子产生一个伪随机数
  3）将伪随机数带入$G(d)$得到高斯随机数
  4）根据输入像素计算出输出像素
  5）重新将像素值放缩在[0~255]之间
  6）循环所有像素
  7）输出图像
  用numpy添加高斯噪声代码如下：

# 随机生成符合正态（高斯）分布的随机数，means,sigma为两个参数
import numpy as np
import cv2
from numpy import shape
import random
import matplotlib.pyplot as plt


def GaussianNoise(src, means, sigma, percetage):
    NoiseImg = src
    NoiseNum = int(percetage * src.shape[0] * src.shape[1])
    for i in range(NoiseNum):
        # 每次取一个随机点
        # 把一张图片的像素用行和列表示的话，randX 代表随机生成的行，randY代表随机生成的列
        # random.randint生成随机整数
        # 高斯噪声图片边缘不处理，故-1
        randX = random.randint(0, src.shape[0] - 1)
        randY = random.randint(0, src.shape[1] - 1)
        # 此处在原有像素灰度值上加上随机数
        NoiseImg[randX, randY] = NoiseImg[randX, randY] + random.gauss(means, sigma)
        # 若灰度值小于0则强制为0，若灰度值大于255则强制为255
        if NoiseImg[randX, randY] < 0:
            NoiseImg[randX, randY] = 0
        elif NoiseImg[randX, randY] > 255:
            NoiseImg[randX, randY] = 255
    return NoiseImg


img = cv2.imread('lenna.png', 0)
img1 = GaussianNoise(img, 2, 4, 0.5)
img = cv2.imread('lenna.png')
b, g, r = cv2.split(img)
img = cv2.merge([r, g, b])
img2 = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# cv2.imwrite('lenna_GaussianNoise.png',img1) # 保存图片
plt.subplot(121), plt.imshow(img2, cmap='gray'), plt.title('lenna_source'), plt.axis('off')
plt.subplot(122), plt.imshow(img1, cmap='gray'), plt.title('lenna_GaussianNoise'), plt.axis('off')
plt.show()

运行结果如下：

椒盐噪声

• 椒盐噪声又称为脉冲噪声，它是一种速记出现的白点或者黑点。
• 椒盐噪声=椒噪声（pepper noise）+盐噪声（salt noise）。检验噪声的值为0（椒）或者255（盐）。
• 前者是低灰度噪声，后者属于高灰度噪声。一般两种噪声同时出现，呈现在图像就是黑白杂点。
• 对于彩色图像，也有可能表现为在单个像素BGR三个通达随机出现的255或0.
• 如果通信时出错，部分像素的值在传输时丢失，就会发生这种噪声。
• 盐和椒噪声的成因可能是受影响讯号受到突如其来的强烈干扰而产生等。例如失效的感应器导致像素值为最小值，饱和的感应器导致像素值为最大值。
  给一幅数字图像加上椒盐噪声的处理顺序：
  1）给定信噪比SNR，其取值范围在[0,1]之间
  2）计算总像素数据SP，得到要加噪的像素数据$NP=SP\ast (1-SNR)$
  3）随机获取要加噪的每个像素位置$(i,j)$
  4）指定像素值为255或者0
  5）重复3,4两个步骤完成所有NP个像素的加噪
  用numpy添加椒盐噪声代码如下：

import numpy as np
import cv2
from numpy import shape
import random
import matplotlib.pyplot as plt


def pepper_salt_noise(src, percetage):
    NoiseImg = src
    NoiseNum = int(percetage * src.shape[0] * src.shape[1])
    for i in range(NoiseNum):  # 返还一个迭代器
        # 每次取一个随机点
        # 把一张图片的像素用行和列表示的话，randX 代表随机生成的行，randY代表随机生成的列
        # random.randint生成随机整数
        # 椒盐噪声图片边缘不处理，故-1
        randX = random.randint(0, src.shape[0] - 1)
        randY = random.randint(0, src.shape[1] - 1)
        # random.random生成随机浮点数，随意取到一个像素点有一半的可能是白点255，一半的可能是黑点0
        if random.random() <= 0.5:
            NoiseImg[randX, randY] = 0
        else:
            NoiseImg[randX, randY] = 255
    return NoiseImg


img = cv2.imread('lenna.png', 0)  # 导入图片
img1 = pepper_salt_noise(img, 0.2)  # 调pepper_salt_noise函数，0.2为参数
# cv2.imwrite('lenna_PepperandSalt.png',img1)  # 在文件夹中写入命名为lenna_PepperandSalt.png的加噪后的图片
img = cv2.imread('lenna.png')
b, g, r = cv2.split(img)
img = cv2.merge([r, g, b])
img2 = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
plt.subplot(121), plt.imshow(img2, cmap='gray'), plt.title('lenna_source'), plt.axis('off')
plt.subplot(122), plt.imshow(img1, cmap='gray'), plt.title('pepper_salt_noise'), plt.axis('off')
plt.show()

运行结果如下：

其他噪声

泊松噪声：复合泊松分布的噪声模型，泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如一服务设施在一定时间内受到的服务请求的次数，电话交换机接到呼叫的次数、汽车站台的候车人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数等等。
乘性噪声：一般有信道不理想引起，他们与信号的关系是相乘，信号在它在，信号不在它也不在。
瑞利噪声：相比高斯噪声而言，其形状向右歪斜，这对于你和某些歪斜直方图噪声很有用。瑞利噪声的实现可以借由平均噪声来实现。
伽马噪声：其分布服从了伽马曲线的分布。伽马噪声的实现，需要使用b个服从指数分布的噪声叠加而来。指数分布的噪声，可以使用均匀分布来实现。（b=1时为指数噪声，b>1时通过若干个实数噪声叠加，得到伽马噪声）
用scikit-image(skimage)添加各种噪声代码如下：

import cv2 as cv
import numpy as np
from PIL import Image
from skimage import util
import matplotlib.pyplot as plt

'''
def random_noise(image, mode='gaussian', seed=None, clip=True, **kwargs):
功能：为浮点型图片添加各种随机噪声
参数：
image：输入图片（将会被转换成浮点型），ndarray型
mode： 可选择，str型，表示要添加的噪声类型
gaussian：高斯噪声
localvar：高斯分布的加性噪声，在“图像”的每个点处具有指定的局部方差。
poisson：泊松噪声
salt：盐噪声，随机将像素值变成1
pepper：椒噪声，随机将像素值变成0或-1，取决于矩阵的值是否带符号
s&p：椒盐噪声
speckle：均匀噪声（均值mean方差variance），out=image+n*image
seed： 可选的，int型，如果选择的话，在生成噪声前会先设置随机种子以避免伪随机
clip： 可选的，bool型，如果是True，在添加均值，泊松以及高斯噪声后，会将图片的数据裁剪到合适范围内。如果谁False，则输出矩阵的值可能会超出[-1,1]
mean： 可选的，float型，高斯噪声和均值噪声中的mean参数，默认值=0
var：  可选的，float型，高斯噪声和均值噪声中的方差，默认值=0.01（注：不是标准差）
local_vars：可选的，ndarry型，用于定义每个像素点的局部方差，在localvar中使用
amount： 可选的，float型，是椒盐噪声所占比例，默认值=0.05
salt_vs_pepper：可选的，float型，椒盐噪声中椒盐比例，值越大表示盐噪声越多，默认值=0.5，即椒盐等量
--------
返回值：ndarry型，且值在[0,1]或者[-1,1]之间，取决于是否是有符号数
'''

img = cv.imread("lenna.png")
b, g, r = cv.split(img)
img = cv.merge([r, g, b])  # 转为RGB
noise_gaussian_img = util.random_noise(img, mode='gaussian')
noise_poisson_img = util.random_noise(img, mode='poisson')
noise_salt_img = util.random_noise(img, mode='salt')
noise_pepper_img = util.random_noise(img, mode='pepper')
noise_sp_img = util.random_noise(img, mode='s&p')
noise_speckle_img = util.random_noise(img, mode='speckle', mean=0.5, var=0.1)
noise_localvar_img = util.random_noise(img, mode='localvar')
plt.subplot(241), plt.imshow(img), plt.title('lenna_source'), plt.axis('off')
plt.subplot(242), plt.imshow(noise_gaussian_img), plt.title('noise_gaussian_img'), plt.axis('off')
plt.subplot(243), plt.imshow(noise_poisson_img), plt.title('noise_poisson_img'), plt.axis('off')
plt.subplot(244), plt.imshow(noise_salt_img), plt.title('noise_salt_img'), plt.axis('off')
plt.subplot(245), plt.imshow(noise_pepper_img), plt.title('noise_pepper_img'), plt.axis('off')
plt.subplot(246), plt.imshow(noise_sp_img), plt.title('noise_sp_img'), plt.axis('off')
plt.subplot(247), plt.imshow(noise_speckle_img), plt.title('noise_speckle_img'), plt.axis('off')
plt.subplot(248), plt.imshow(noise_localvar_img), plt.title('noise_localvar_img'), plt.axis('off')
plt.show()

运行结果如下：

图像滤波

1、图像滤波，即在尽量保留细节特征的条件下对目标图像的噪声进行抑制，是图像预处理中不可缺少的操作，其处理效果的好坏直接影响到后续图像处理和分析的有效性和可靠性。
2、消除图像中的噪声成分叫做图像的平滑化和滤波操作。信号或图像的能量大部分集中在幅度谱的低频和中频断是很常见的，而在较高频段，感兴趣的信息经常被噪声研磨。因此一个能降低高频成分幅度的滤波器就能够减弱噪声的影响。
3、平滑滤波是低频增强的空间域滤波技术。它的目的有两类：一类是模糊；另一类是消除噪音。空间域的平滑滤波一般采用简单平均法进行，就是求临近像素点的平均亮度值。邻域的大小和平滑的效果直接相关，因此邻域越大平滑的效果越好，但邻域越大，平滑会使边缘信息损失的越大，从而使输出的图像变得模糊，因此需要合理的选择邻域的大小。
4、关于滤波器，一种形象的比喻是：我们可以把滤波器想象成一个包含加权系数的窗口，当使用这个滤波器平滑处理图像时，就把这个窗口放到图像智商，透过这个窗口来看我们得到的图像。
线性滤波可以说是图像处理最基本的方法，它可以允许我们对图像进行处理，产生很多不同的效果。

滤波的目的

1、消除图形中混入的噪声；
2、为图像识别抽取出图像特征。

滤波的要求

1、不能损坏图像轮廓即边缘
2、图像视觉效果应当更好

各种滤波器

均值滤波

均值滤波，是图像处理中最常用的手段，从频率域观点来看均值滤波就是一种低通滤波器，高频信号将会去掉，因此可以版主消除图像尖锐噪声，实现图像平滑，模糊等功能。理想的均值滤波是每个像素和它周围像素计算出来的平均值替换图像中的每个像素。
$$g(x,y)=\frac{1}{M}\sum _{f\in s}f(x,y)$$

• 从左到右丛生倒下计算图像中的每个像素，最终得到处理后的图像。
• 均值滤波可以加上两个参数，即迭代次数，Kernel数据大小。
• 一个相同的kernel，但是多次迭代就会效果越来越好。
• 同样，迭代次数相同，kernel矩阵越大，均值滤波的效果越明显。
  优点：算法简单，计算速度快；
  缺点：降低噪声的同时使图像产生模糊，特别是景物的边缘和细节部分。

中值滤波

中值滤波也是消除图像噪声最常见的手段之一，特别是消除椒盐噪声，中值滤波的效果要比均值滤波更好。中值滤波根据智滤波唯一不同是，不是同均值滤波来替换中心每个像素，而是将周围像素中和中心像素排序后，取中值。
一个3x3带下的中值滤波如下：

优点：抑制效果很好，画面的清晰度基本保持；
缺点：对高斯噪声的抑制效果不是很好。

最大最小值滤波

最大最小值滤波是一种比较保守的图像处理手段，与中值滤波类似，首先要排序周围像素和中心像素值，然后江中心像素值与最大和最小值比较，如果比最小值小，则替换中心像素为最小值，如果中心像素比最大值大，则替换中心像素为最大值。
一个kernel矩阵为3x3的最大最小值滤波如下：

双边滤波

一种同时考虑了像素空间差异与强度差异的滤波器，因此具有保持图像边缘的特性。
先看看高斯滤波器：
$$W_{ij}=\frac{1}{K_i}exp\left(-\frac{{\left|x_j-x_i\right|}^2}{{\sigma }^2}\right)$$
其中W是权重，i和j是像素索引。公式中可以看出，权重和像素之间的空间距离有关系，无论图像的内容是什么，都有相同的滤波效果。
再看看双边滤波器，它只是在原有高斯函数的基础上加了一项：
$$W_{ij}=\frac{1}{K_i}exp\left(-\frac{{\left|x_j-x_i\right|}^2}{{\sigma }^2}\right)\left(-\frac{{\left|I_j-I_i\right|}^2}{{\sigma }^2}\right)$$
其中I是像素的强度值，所以在强度差距较大的地方（边缘），权重会减小，滤波效应也就变小。总体而言，就像素强度变换不大的区域，双边滤波有类似于高斯滤波的效果，而在图像边缘等强度梯度较大的地方，可以保持梯度。

限幅滤波（程序判断滤波）

• 方法：根据经验判断，确定两次采用允许的最大偏差值（设置为top）每次检测到新值时判断：如果本次值与上次值之差<=top，则本次值有效，如果本次值与上次值之差>top，则本次值无效，放弃本次值，用上次值代替本次值
• 优点：能有效克服因偶然因素引起的脉冲干扰
• 缺点：无法抑制周期性的干扰，平滑度差

引导滤波

• 与双边滤波最大的相似之处，就是同样具有保持边缘特性，在引导滤波的定义中，用到了局部现行模型
• 该模型认为，某函数在一点与其邻近部分的点成线性关系，一个复杂的函数就可以用很多局部的线性函数表示，当需要求该函数某一点的值时，只需要计算所办函该店的现行函数的值并做平均即可。这种模型，在表示分解析函数上，非常有用。
  
  同理，我们可以认为图像是一个二维函数，而且没发写成解析表达式，我们因此假设干函数的输出与输入在一个二维窗口内满足线性关系：$$q_i=a_k{I}_i+b_k,\forall i\in {\omega }_k$$其中，q是输出像素的值，I是输入图像的值，i和k是像素索引，a和b是当窗口中心位于k时该现行函数的系数。其实，输入图像不一定是待滤波的图像本身，也可以是其他图像即引导图像，这也是为何称为引导滤波的原因，对上式两边取梯度，可以得到：$$\nabla q=a\nabla I$$即当输入图像I有梯度是，输出q也有类似的梯度，现在可以解释为什么引导滤波有边缘保持特性了。
  下一步是求出线性函数的系数，也就是线性回归，即希望你和函数的输出值与真实值p之间的差距最小，也就是让下式最小：
  $$E(a_k,b_k)=\sum _{i\in {\omega }_k}\left({\left(a_k{I}_i+b_k-p_i\right)}^2+\epsilon a_k^2\right)$$
  这里的p只能是待求滤波图像，并不想I那样可以使其他图像。同时，a之前的系数（以后都写为$\epsilon$）用于防止求得的a过大，也是调节滤波器效果的重要参数。通过最小二乘法，可以得到：
  $$\{\begin{array}{l}{a}_k=\frac{\frac{1}{\left|\omega \right|}\sum _{i\in {\omega }_k}{I}_i{p}_i-{\mu }_k{\overline{p}}_k}{{\sigma }_k^2+\epsilon }\\ b_k={\overline{p}}_k-a_k{\mu }_k\end{array}$$
  其中，${\mu }_k$是I在${\omega }_k$中的平均值，${\sigma }_k^2$是I在窗口${\omega }_k$中的方差，$\left|\omega \right|$是窗口${\omega }_k$中像素的数量，${\overline{p}}_k$是带滤波图像p在窗口${\omega }_k$中的均值。
  在计算每个窗口的线性系数关系是，我们可以发现一个像素会被多个窗口包含，也就是说，每个像素都由多个现行函数所描述。因此，如之前所说，要具体求某一点的输出值时，只需将所有包含该店的现行函数值平均即可：
  $$q_i=\frac{1}{\left|\omega \right|}\sum _{k:i\in {\omega }_k}\left(a_k{I}_k+b_k\right)={\overline{a}}_i{I}_i+{\overline{b}}_i$$这里，${\omega }_k$是所有包含像素i的窗口，k是其中心位置。
  当把引导式滤波用作边缘保持滤波器时，往往有$I=p$，如果$\epsilon =0$，显然$a=1,b=0$是$E(a,b)$为最小值的解，从上式可以看出，这是的滤波器没有任何作用，将输入原封不动地输出。如果$\epsilon >0$，在像素强度变化晓得区域（或单色区域），有a近似于（或等于）0，而b近似于（或等于），即做了一个加权均值滤波；而在变化大的区域，a近似于1，b近似于0，对图像的滤波效果很弱，有助于保持边缘。而$\epsilon$的作用就是界定什么是变化大，什么是变化小。在窗口大小不变的情况下，随着$\epsilon$的增大，滤波效果越明显。
  从滤波效果上，引导滤波和双边滤波差不多，采一些细节上，引导滤波较好。
  引导滤波最大的优势在于，可以写出事件福再度和窗口大小无关的算法，因此在使用大窗口处理图片时，其效果更高。

图像增强

图像增强可以分为两种：

• 点处理技术。只对单个像素进行处理。
• 领域处理技术。对像素点及其周围的点进行处理，即使用卷积核。

点处理

1、线性变换

图像增强现性变换主要对图像的对比度和亮度进行调整$$y=ax+b$$参数a影响图像的对比度，参数b影响图像的亮度，具体可分为以下几种情况：
$a>1$：增强图像的对比度，图像看起来更加清晰
$a<1$：减小了图像的对比度，图像看起来变模糊
$a=1andb\ne 0$：图像整体的灰度值上移或者下移，也就是图像整体变亮或者变暗，不会改变图像的对比度，$b>0$时图像变亮，$b<0$时图像变暗
$a=-1andb=255$：图像翻转

2、分段线性变换

即对处于某个感兴趣的区域x，将其对比系数a增大或减小，从而增大或减小这个区域的对比度。
$$\{\begin{array}{l}y=a_{1}x+bx<x_1\\ y=a_{2}x+b{x}_1<x<x_2\\ y=a_{3}x+b{x}_2<x\end{array}$$

3、对数变换

对数变换讲=将图像的灰度值部分扩展，即将高灰度部分压缩，已达到增强图像低灰度部分的目的，同时可以很好地压缩像素值变化较大的图像的动态范围，目的就是突出我们需要的细节。
$$y=c\log (1+x)$$

4、幂律变换/伽马变换

幂律变换主要用于图像的矫正，对漂白的图片或者过黑的图片可以进行修正。$$y=c{x}^{\gamma }$$根据$\gamma$的大小，主要可分为以下两种情况：
$\gamma >1$：处理漂白的图片，进行灰度级压缩
$\gamma <1$：处理过黑的图片，对比度增强，是的细节看的更加清楚。

领域处理

直方图均值化
图像滤波

OpenCV算法解析

OpenCV

• OpenCV是一个开源的计算机视觉库，可以从OnpenCV官网获取
• OpenCV库用C语言和C++语言编写，可以在windows、linux、mac OS X等系统运行。同事也在积极开发Python、Java、Mtatlab以及其他一些语言的接口，将库导入安卓和ios中为移动设备开发应用。
• OpenCV设计用于进行高效的计算，十分强调实时应用的开发。它由C++语言编写并进行了深度优化，从而可以享受多线程处理的优势。
• OpenCV的一个目标识提供易于使用的计算机视觉接口，从而帮助人们快速建立精巧的视觉应用。
• OpenCV库包含从计算机视觉各个领域衍生出来的500多个函数，包括工业产品质量检验、医学图像处理、安保领域、交互领域、相机矫正、双目视觉以及机器人学。

OpenCV大坑之BGR

opencv对于读进来的图片的通道排列是BGR，而不是主流的RGB！谨记！

# opencv读入的矩阵是BGR，可用如下代码转为RGB
img = cv2.imread("lena.png")
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

1、除了opencv读入的彩色图片以BGR顺序存储外，其他所有图像库读入彩色图片都已RGB存储。
2、除了PIL读入图片时img类之外，其他库读进来的图都是numpy矩阵形式。
3、各大图像库的性能，最好的OpenCV，无论是速度还是图片操作的全面性，都属于碾压的存在，毕竟它是一个巨大的cv专用库。

OpenCV常见算法

1、图像的基本曹组读取、显示、存储：通过调用opencv中的cv2.imread()，cv2.imshow()，cv2.write()分别实现；
2、在opencv中实现将彩色像素转化为灰度像素。
3、图像的几何变换：平移、缩放、旋转、插值（最邻近、双线性）
4、对比增强：线性变换、伽马变换、直方图均衡化
5、边缘检测：Sobel、Laplace、Canny
6、图像的二维滤波：cvFilter2D

最小二乘法(Least Square Method)

什么是线性行回归？
举个例子，某商品的利润在售价为2元、5元、10元时分别为4元、10元、20元。我们很容易得出商品利润与售价的关系复合直线：$y=2x$.
在上面这个简单的一元线性回归方程中，我们称“2”为回归系数，即斜率为回归系数。回归系数表示商品的售价（x）每变动一个单位，期利润（y）与之对应的变动关系。

线性回归表示这些离散的点总体上最逼近哪条直线。

• 它通过最小化误差的平方和，寻找数据的最佳函数匹配。
• 利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和最小。
• 假设我们现在有一些类的数据点$(x_i,y_i)(i=1,\cdots ,m)$，那么由我们给出的你和函数$h(x)$得到的估计量就是$h(x_i)$
• 残差$r_i=h(x_i)-y_i$
  由此，我们可以写出最小二乘法的定义了：
  $$\underset{a,b}{\min }\sum _{n=1}^N(y_n-{(k\times x+b))}^2$$
  这是一个无约束的最优化问题，分别对k和b求骗到，然后零偏导数为0，即可获得极值点。
  $$\{\begin{array}{l}k=\frac{N{\sum }_{n=1}^N{x}_n\times y_n-\left({\sum }_{n=1}^N{x}_n\right)\left({\sum }_{n=1}^N{y}_n\right)}{\left(N{\sum }_{n=1}^N{\left(x_n\right)}^2-{\left({\sum }_{n=1}^N{x}_n\right)}^2\right)}\\ b=\frac{{\sum }_{n=1}^N{y}_n}{N}-k\frac{{\sum }_{n=1}^N{x}_n}{N}\end{array}$$
  对train_data.csv中数据（如下）进行最小二乘法，代码如下：
  

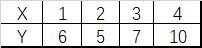
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

sales = pd.read_csv('train_data.csv', sep=r'\s*,\s*', engine='python')  # 读取CSV
X = sales['X'].values  # 存csv的第一列
Y = sales['Y'].values  # 存csv的第二列


def get_data(slope, intercept, x_lim):
    x_vals = np.array(x_lim)
    y_vals = intercept + slope * x_vals
    return x_vals, y_vals


# 初始化赋值
s1 = 0
s2 = 0
s3 = 0
s4 = 0
n = 4  # 你需要根据的数据量进行修改

# 循环累加
for i in range(n):
    s1 = s1 + X[i] * Y[i]  # X*Y，求和
    s2 = s2 + X[i]  # X的和
    s3 = s3 + Y[i]  # Y的和
    s4 = s4 + X[i] * X[i]  # X**2，求和

# 计算斜率和截距
k = (s2 * s3 - n * s1) / (s2 * s2 - s4 * n)
b = (s3 - k * s2) / n
print("Slope: {} Intercept: {}".format(k, b))
xx, yy = get_data(k, b, [min(X)-1, max(X)+1])

plt.scatter(X, Y, marker='.', color='red', s=40, label='original point')
plt.plot(xx, yy, 'b', label='least_square'), plt.title('least_square'), plt.xlim(min(X)-1, max(X)+1)
plt.legend(loc='best')
plt.show()

运行结果如下：

Slope: 1.4 Intercept: 3.5

RANSAC

• 随机采样一致性（random sample sonsensus）
• RANSAC是一种思想，一个求解已知模型的参数的框架。它不限定某一特定的问题，可以使计算机视觉的问题，同样也可以是统计学问题，甚至可以使经济学领域的模型参数估计问题。
• 它是一种迭代方法，用来在一组包含离群的被观测数据中估算处数学模型的参数。RANSAC是一个非确定性算法，在某种意义上说，它产生一个在一定概率下合理的结果，其允许使用更多次的迭代算法来使其概率增加。
• RANSAC的基本假设是“内群”数据可以通过机组模型参数来叙述其数据分布，而“离群”数据则是不适合模型化的数据。数据会受噪声影响，噪声指的是离群，例如从极端的噪声或错误结社有关数据的测量或不正确的假设。RANSAC假定，给定一组（通常很小的）内存，存在一个程序，这个程序可以估算最佳解释或最适用于这一数据模型的参数。
  

RANSAC与最小二乘法

• 生产实践中的数据往往有一定的偏差。
• 例如我们知道两个变量X和Y之间成线性关系，$Y=aX+b$，我们想确定参数a和b的具体指，通过实验，可以得到一组X与Y的测试值。虽然理论上两个未知数的方程只需要两组值即可确认，但由于系统误差的原因，任意取两点算出的a与b的值都不尽相同。我们希望的是，最后计算得出的理论模型与测试值的误差最小。
• 最小二乘法：通过计算最小均房误差关于参数a、b的偏导数为零时的值。事实上，很多情况下，最小二乘法都是线性回归的代名词。
• 遗憾的是，最小二乘法只适合于误差较小的情况。
• 在模型确定以及最大迭代次数允许的情况下，RANSAC总能找到最优解。（对于包含80%误差的数据集，RANSAC的效果远优于直接的最小二乘法。）
• 由于一张图片中像素点数最大，采用最小二乘法运算量大，计算速度慢。
  

RANSAC的步骤

RANSAC算法的输入：
1、一组观测数据（往往含有较大的噪声或无效点），
2、一个用于解释观测数据的参数化模型
3、一些可信的参数
RANSAC算法的步骤：
1、在数据中随机选择几个点设定为内群
2、计算适合内群的模型
3、把其他刚才没选到的点带入刚才建立的模型汇总，计算是否为内群
4、记下内群数量
5、重复以上步骤
6、比较哪次计算中内群数量最多，内群数量最多的哪次所建的模型就是我们所要求的解
注意：不同问题对应的数学模型不同，英雌在计算模型参数是方法必定不同，RANSAC的作用不在于计算模型参数，而是提供更好的输入数据（样本）。（这是ransac的缺点在于要求数学模型已知）
其代码实现如下：

import numpy as np
import scipy as sp
import scipy.linalg as sl


def ransac(data, model, n, k, t, d, debug=False, return_all=False):
    """
    输入:
        data - 样本点
        model - 假设模型:事先自己确定
        n - 生成模型所需的最少样本点
        k - 最大迭代次数
        t - 阈值:作为判断点满足模型的条件
        d - 拟合较好时,需要的样本点最少的个数,当做阈值看待
    输出:
        bestfit - 最优拟合解（返回nil,如果未找到）

    iterations = 0
    bestfit = nil #后面更新
    besterr = something really large #后期更新besterr = thiserr
    while iterations < k
    {
        maybeinliers = 从样本中随机选取n个,不一定全是局内点,甚至全部为局外点
        maybemodel = n个maybeinliers 拟合出来的可能符合要求的模型
        alsoinliers = emptyset #满足误差要求的样本点,开始置空
        for (每一个不是maybeinliers的样本点)
        {
            if 满足maybemodel即error < t
                将点加入alsoinliers
        }
        if (alsoinliers样本点数目 > d)
        {
            %有了较好的模型,测试模型符合度
            bettermodel = 利用所有的maybeinliers 和 alsoinliers 重新生成更好的模型
            thiserr = 所有的maybeinliers 和 alsoinliers 样本点的误差度量
            if thiserr < besterr
            {
                bestfit = bettermodel
                besterr = thiserr
            }
        }
        iterations++
    }
    return bestfit
    """
    iterations = 0
    bestfit = None
    besterr = np.inf  # 设置默认值
    best_inlier_idxs = None
    while iterations < k:
        maybe_idxs, test_idxs = random_partition(n, data.shape[0])
        print('test_idxs = ', test_idxs)
        maybe_inliers = data[maybe_idxs, :]  # 获取size(maybe_idxs)行数据(Xi,Yi)
        test_points = data[test_idxs]  # 若干行(Xi,Yi)数据点
        maybemodel = model.fit(maybe_inliers)  # 拟合模型
        test_err = model.get_error(test_points, maybemodel)  # 计算误差:平方和最小
        print('test_err = ', test_err < t)
        also_idxs = test_idxs[test_err < t]
        print('also_idxs = ', also_idxs)
        also_inliers = data[also_idxs, :]
        if debug:
            print('test_err.min()', test_err.min())
            print('test_err.max()', test_err.max())
            print('numpy.mean(test_err)', numpy.mean(test_err))
            print('iteration %d:len(alsoinliers) = %d' % (iterations, len(also_inliers)))
        # if len(also_inliers > d):
        print('d = ', d)
        if (len(also_inliers) > d):
            betterdata = np.concatenate((maybe_inliers, also_inliers))  # 样本连接
            bettermodel = model.fit(betterdata)
            better_errs = model.get_error(betterdata, bettermodel)
            thiserr = np.mean(better_errs)  # 平均误差作为新的误差
            if thiserr < besterr:
                bestfit = bettermodel
                besterr = thiserr
                best_inlier_idxs = np.concatenate((maybe_idxs, also_idxs))  # 更新局内点,将新点加入
        iterations += 1
        if bestfit is None:
            raise ValueError("did't meet fit acceptance criteria")
        if return_all:
            return bestfit, {'inliers': best_inlier_idxs}
        else:
            return bestfit


def random_partition(n, n_data):
    """return n random rows of data and the other len(data) - n rows"""
    all_idxs = np.arange(n_data)  # 获取n_data下标索引
    np.random.shuffle(all_idxs)  # 打乱下标索引
    idxs1 = all_idxs[:n]
    idxs2 = all_idxs[n:]
    return idxs1, idxs2


class LinearLeastSquareModel:
    # 最小二乘求线性解,用于RANSAC的输入模型
    def __init__(self, input_columns, output_columns, debug=False):
        self.input_columns = input_columns
        self.output_columns = output_columns
        self.debug = debug

    def fit(self, data):
        # np.vstack按垂直方向（行顺序）堆叠数组构成一个新的数组
        A = np.vstack([data[:, i] for i in self.input_columns]).T  # 第一列Xi-->行Xi
        B = np.vstack([data[:, i] for i in self.output_columns]).T  # 第二列Yi-->行Yi
        x, resids, rank, s = sl.lstsq(A, B)  # residues:残差和
        return x  # 返回最小平方和向量

    def get_error(self, data, model):
        A = np.vstack([data[:, i] for i in self.input_columns]).T  # 第一列Xi-->行Xi
        B = np.vstack([data[:, i] for i in self.output_columns]).T  # 第二列Yi-->行Yi
        B_fit = sp.dot(A, model)  # 计算的y值,B_fit = model.k*A + model.b
        err_per_point = np.sum((B - B_fit) ** 2, axis=1)  # sum squared error per row
        return err_per_point


def test():
    # 生成理想数据
    n_samples = 500  # 样本个数
    n_inputs = 1  # 输入变量个数
    n_outputs = 1  # 输出变量个数
    A_exact = 20 * np.random.random((n_samples, n_inputs))  # 随机生成0-20之间的500个数据:行向量
    perfect_fit = 60 * np.random.normal(size=(n_inputs, n_outputs))  # 随机线性度，即随机生成一个斜率
    B_exact = sp.dot(A_exact, perfect_fit)  # y = x * k

    # 加入高斯噪声,最小二乘能很好的处理
    A_noisy = A_exact + np.random.normal(size=A_exact.shape)  # 500 * 1行向量,代表Xi
    B_noisy = B_exact + np.random.normal(size=B_exact.shape)  # 500 * 1行向量,代表Yi

    if 1:
        # 添加"局外点"
        n_outliers = 100
        all_idxs = np.arange(A_noisy.shape[0])  # 获取索引0-499
        np.random.shuffle(all_idxs)  # 将all_idxs打乱
        outlier_idxs = all_idxs[:n_outliers]  # 100个0-500的随机局外点
        A_noisy[outlier_idxs] = 20 * np.random.random((n_outliers, n_inputs))  # 加入噪声和局外点的Xi
        B_noisy[outlier_idxs] = 50 * np.random.normal(size=(n_outliers, n_outputs))  # 加入噪声和局外点的Yi
    # setup model
    all_data = np.hstack((A_noisy, B_noisy))  # 形式([Xi,Yi]....) shape:(500,2)500行2列
    input_columns = range(n_inputs)  # 数组的第一列x:0
    output_columns = [n_inputs + i for i in range(n_outputs)]  # 数组最后一列y:1
    debug = False
    model = LinearLeastSquareModel(input_columns, output_columns, debug=debug)  # 类的实例化:用最小二乘生成已知模型

    linear_fit, resids, rank, s = sp.linalg.lstsq(all_data[:, input_columns], all_data[:, output_columns])

    # run RANSAC 算法
    ransac_fit, ransac_data = ransac(all_data, model, 50, 1000, 7e3, 300, debug=debug, return_all=True)

    if 1:
        import pylab

        sort_idxs = np.argsort(A_exact[:, 0])
        A_col0_sorted = A_exact[sort_idxs]  # 秩为2的数组

        if 1:
            pylab.plot(A_noisy[:, 0], B_noisy[:, 0], 'k.', label='data')  # 散点图
            pylab.plot(A_noisy[ransac_data['inliers'], 0], B_noisy[ransac_data['inliers'], 0], 'bx',
                       label="RANSAC data")
        else:
            pylab.plot(A_noisy[non_outlier_idxs, 0], B_noisy[non_outlier_idxs, 0], 'k.', label='noisy data')
            pylab.plot(A_noisy[outlier_idxs, 0], B_noisy[outlier_idxs, 0], 'r.', label='outlier data')

        pylab.plot(A_col0_sorted[:, 0],
                   np.dot(A_col0_sorted, ransac_fit)[:, 0],
                   label='RANSAC fit')
        pylab.plot(A_col0_sorted[:, 0],
                   np.dot(A_col0_sorted, perfect_fit)[:, 0],
                   label='exact system')
        pylab.plot(A_col0_sorted[:, 0],
                   np.dot(A_col0_sorted, linear_fit)[:, 0],
                   label='linear fit')
        pylab.legend()
        pylab.show()


if __name__ == "__main__":
    test()

运行结果如下：

RANSAC的参数确定

• 假设每个点是真正内群的概率为$w$：$w=\frac{内群数目}{内群数目+外群数目}$
• 通常我们不知道$w$是多少，$w^n$是所选择的n个点都是内群的几率，$1-w^n$是所选择的n个点至少一个不是内群的几率，$(1-w^n{)}^k$是表示重复k此都没有全部的n个点都是内群的几率，假设算法跑k此以后成功的几率是p，那么
  $$\{\begin{array}{l}1-p={(1-w^n)}^k\\ p={1-(1-w^n)}^k\end{array}$$
• 我们可以通过p反算得到抽取次数k，$k=\frac{\log (1-p)}{\log (1-w^n)}$
• 所以如果希望成功几率高，当n不变时，k越大，则p越大；当w不变时，n越大，所学的k就越大，通常w未知，所以n选小一点比较好。

RANSAC的应用

全景拼接

1、针对某个场景拍摄多张/序列图像
2、通过匹配特征（sift匹配）计算下一张图像与上一张图像之间的变换结构。
3、图像映射，将下一张图像叠加到上一张图像的坐标系中
4、变换后的融合/合成

RANSAC的优缺点

优点：
1、它能鲁棒的估计模型参数。例如，他能从包含大量局外点的数据集中估计出高精度的参数。
缺点：
1、它计算参数的迭代次数没有上限；如果设置迭代次数上限，得到的结果可能不是最优的结果，甚至可能得到错误的结果；
2、只有一定的概率得到可信的模型，概率与迭代次数成正比；
3、它要求实则根问题相关的阈值；
4、RACSAC智能从特定数据集中估计出一个模型，如果存在两个（或多个模型），RACSAC不能找到别的模型；
5、要求数学模型已知。

哈希算法

图像相似度比较哈希算法

哈希的相关概念

• 散列函数（或散列算法，又称哈希函数：Hash Function）是一种从任何一种数据中创建小的数字“指纹”的方法。散列函数把消息或数据压缩成摘要，使得数据量变小，将数据的格式固定下来。该函数将数据打乱混合，重新创建一个叫做散列值（hase values、hash codes、hash nums、hashes）的指纹。散列值通常用一个短的随机字母和数字组成字符串来代表。
• 通过哈希算法得到的任意长度的二进制值映射为较短的固定长度的二进制值，即哈希值。此外，哈希值是一段数据唯一且及其紧凑的数值表示形式，如果通过哈希一段明文得到哈希值，哪怕只更改该明文中的任意一个字母，随后得到的哈希值都将不同。
• 哈希算法是一个函数，能够把几乎所有的数字文件都转换成一串由数字和字母构成的看似乱码的字符串。

哈希的特点

哈希算法作为一种加密函数，其拥有两个最重要的特点：
1、不可逆性。输入信息得出输出的那个看似乱码的字符串（哈希值）非常容易，但是从输出的字符反推处输入的记过却非常非常困难。
2、输出值唯一性和不可预测性。只要输入的信息有一点点区别，那么根据哈希算法得出来的输出值也相差甚远。

汉明距离

两个整数之间的汉明距离指的是这两个数字对应二进制不同的位置的数目。
例：输入：x=1，y=4 ；输出：2

1、均值哈希算法

1、缩放：图片所防伪8*8，保留结构，删除细节。
2、灰度化：转化为灰度图。
3、求平局值：计算灰度图所有像素的平均值。
4、比较：像素值大于平均值记作1，相反记作0，总共64位。
5、生成哈希：将上述步骤生成的1和0按顺序组合起来就是图片的指纹
6、对比指纹：将两幅图的指纹对比，计算汉明距离，即两个64位的hash值有多少位是不一样的，不相同位数越少，图片越相似。

2、差值哈希算法

差值哈希算法相较于均值哈希算法，前期和后期基本相同，只有中间比较hash有变化。
1、缩放：图片所防伪8*9，保留结构，删除细节。
2、灰度化：转化为灰度图。
3、求平局值：计算灰度图所有像素的平均值。
4、比较：像素值大于后一个像素值记作1，相反记作0。本行不予下一行做对比，每行9个像素，八个差值，有8行，总共64位。
5、生成哈希：将上述步骤生成的1和0按顺序组合起来就是图片的指纹
6、对比指纹：将两幅图的指纹对比，计算汉明距离，即两个64位的hash值有多少位是不一样的，不相同位数越少，图片越相似。

3、感知哈希算法

均值哈希算法过于严格，不够精确，更适合搜索缩略图，为了获得更精准的记过可以选择感知哈希算法，它采用的是DCT(离散余弦变换）来降低频率的方法。

DCT(离散余弦变换）

• 离散余弦变换（Discrete Cosine Transform），主要用于将数据或图像的压缩，能够将空域的信号转换到频域上，具有良好的去相关性的性能。
• DCT变换本身是无损的，同时由于DCT变换是对称的，所以，我们可以在量化编码后利用DCT反变换，在接收断恢复原始的图像信息。
• DCT变换在当前的图像分析以及压缩领域有着极为广大的用途，我们常见的JPEG静态图像编码以及MJPEG、MPEG动态编码等标准中都使用了DCT变换。
  $$\begin{gathered} F\left(u,v\right)=c(u)c(v){\sum }_{i=0}^{N-1}{\sum }_{j=0}^{N-1}f(i,j)\cos \left[\frac{(i+0.5)\pi }{N}u\right]\cos \left[\frac{(j+0.5)\pi }{N}v\right] \\ c(u)=\{\begin{array}{l}\sqrt{\frac{1}{N}},u\ne 0\\ \sqrt{\frac{2}{N}},u=0\end{array}c(v)=\{\begin{array}{l}\sqrt{\frac{1}{N}},v\ne 0\\ \sqrt{\frac{2}{N}},v=0\end{array} \end{gathered}$$
  其中,
• $F(u,v)$是输出的变换结果；
• $N$为原始信号的点数
• $f(i,j)$是原始图像点$(i,j)$的像素值
• $c(u),c(v)$是DCT系数
  
  应用举例：
  某个图像的一个8*8方块的亮度值如下。为了减少绝对值波动，先把数值移位以下，变成-128~127。
  
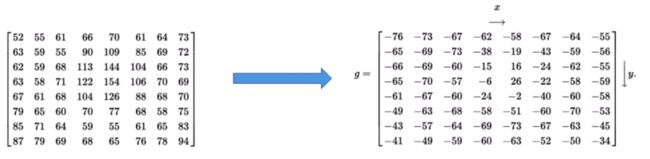
  根据DCT变换公式，计算结果如下：
  
  DCT在JPEG压缩编码中的应用：
  JPEG(Joint Photographic Experts Group)专家组开发了两种基本的压缩算法，一种是采用离散余弦变换（DCT）为基础的有损压缩算法，另一种是采用以预测技术为基础的无损压缩算法。使用有损压缩算法时，在压缩比为25:1情况下，压缩后还原得到的预想与原始图像相比较，非图像专家难于找出他们之间的区别，因此得到了广泛的应用。
  
  DCT在数字水印（digital watermarking）技术中的应用：
  数字水印技术是将特定的信息嵌入到数字信息的内容中，要求嵌入的信息不能被轻易的去除，茄子一定条件下可以被提出出来，已确认作者的版权。
  

感知哈希算法具体步骤

1、缩小图片：3232是一个比较好的大小，这样方便DCT计算；
2、转化为灰度图：把缩放后的图片转换为灰度图；
3、计算DCT：DCT把图片分离成分率的几何；
4、缩小DCT：DCT计算后的矩阵是3232，保留左上角的8*8，这些图片代表图片的最低频率；
5、计算平均值：计算缩小DCT后所有像素点的平均值；
6、进一步减小DCT：大于平均值记录为1，反之记录为0；
7、得到信息指纹：组合64个信息为，顺序随意保持一致性；
8、最后比对两张图片的指纹，获得汉明距离即可。

4、三种哈希算法的比较

• aHash：均值哈希。速度比较快，但常常不太精准。
• pHash：感知哈希。精确度较高，但是速度方面较差一些。
• dHash：插值哈希，精确度较高，且速度也比较快。
• 均值哈希本质是对颜色的比较
• 感知哈希由于做了DCT操作，本质上是对频率的比较
• 插值哈希本质上是与渐变的感知哈希算法
  均值哈希与感知哈希算法代码如下：

import cv2
import numpy as np


# 均值哈希算法
def aHash(img):
    # 缩放为8*8
    img = cv2.resize(img, (8, 8), interpolation=cv2.INTER_CUBIC)
    # 转换为灰度图
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    # s为像素和初值为0，hash_str为hash值初值为''
    s = 0
    hash_str = ''
    # 遍历累加求像素和
    for i in range(8):
        for j in range(8):
            s = s + gray[i, j]
    # 求平均灰度
    avg = s / 64
    # 灰度大于平均值为1相反为0生成图片的hash值
    for i in range(8):
        for j in range(8):
            if gray[i, j] > avg:
                hash_str = hash_str + '1'
            else:
                hash_str = hash_str + '0'
    return hash_str


# 差值感知算法
def dHash(img):
    # 缩放8*9
    img = cv2.resize(img, (9, 8), interpolation=cv2.INTER_CUBIC)
    # 转换灰度图
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    hash_str = ''
    # 每行前一个像素大于后一个像素为1，相反为0，生成哈希
    for i in range(8):
        for j in range(8):
            if gray[i, j] > gray[i, j + 1]:
                hash_str = hash_str + '1'
            else:
                hash_str = hash_str + '0'
    return hash_str


# Hash值对比
def cmpHash(hash1, hash2):
    n = 0
    # hash长度不同则返回-1代表传参出错
    if len(hash1) != len(hash2):
        return -1
    # 遍历判断
    for i in range(len(hash1)):
        # 不相等则n计数+1，n最终为相似度
        if hash1[i] != hash2[i]:
            n = n + 1
    return n


img1 = cv2.imread('lenna.png')
img2 = cv2.imread('lenna_noise.png')
hash1 = aHash(img1)
hash2 = aHash(img2)
print(hash1)
print(hash2)
n = cmpHash(hash1, hash2)
print('均值哈希算法相似度：', n)
hash1 = dHash(img1)
hash2 = dHash(img2)
print(hash1)
print(hash2)
n = cmpHash(hash1, hash2)
print('差值哈希算法相似度：', n)

运行结果如下：

1011111010011110100111011010100110101011101000110000111000101100
1011011010011110100111011010100110101011101000111010111000101100
均值哈希算法相似度： 3
1000100110001101101000101010010001000110111011001010010110000011
1001100110001101100000101110010011000110011011000010010111000011
差值哈希算法相似度： 7