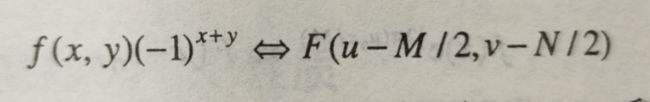数字图像处理第四章频率域滤波（低通滤波器、高通滤波器、拉普拉斯滤波、同态滤波器）

本章节的主要内容具体包括：傅里叶变换的概念及处理的相关知识、频率域卷积概念、三种低通滤波器的原理及代码实现、三种高通滤波器的原理及代码实现、频率域拉普拉斯算法原理及实现、同态滤波器原理及代码实现。

4.1傅里叶变换原理

频率域图像处理步骤：

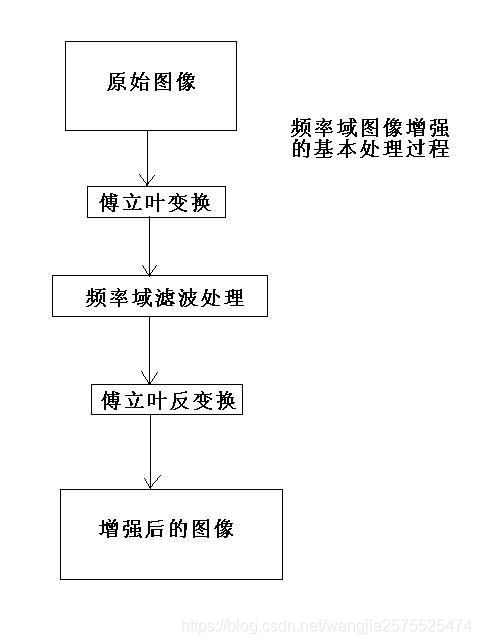
在具体进行频率域的各种处理滤波的前后,进行了傅立叶变换以及傅立叶反变换.这两个变换的过程就是将空间的信息分解为在频率上的表示,或者将频率上的表示转化为空间上的表示,两种变换是互为逆变换的.正是通过傅立叶正反变换的处理,才使得频率域上的处理可以用于图像的增强。

1、傅里叶变换

概念：
法国数学家傅里叶指出：任何周期函数都可以表示为不同频率的正弦和或余弦和的形式，每个正弦和或者余弦和乘以不同的系数（这个正弦和或余弦和就是傅里叶级数）。
非周期函数也可以用正弦或者余弦乘以加权函数的积分来表示。这种情况下就是傅里叶变换。。DFT指的是单变量的离散傅里叶变化；
公式：（二维离散形式）
正变换：

反变换：

图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。直流分量 [公式] 对应一幅图像的平均灰度，低频对应图像中变化缓慢的灰度分量，高频部分对应图像边缘和灰度级突变的部分。

2、频率域卷积–卷积定理

首先在空间域中，两个函数的卷积涉及一个函数关于原点做翻转（旋转180度）并划过另一个函数，在滑动在过程中在每一个位移处我们都做计算，在空间域中是做乘积之和；
而在频率域中，两个连续函数在卷积变为求积分：

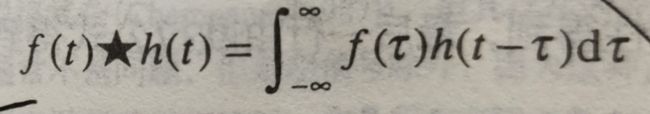
然后我们利用傅里叶变换将函数扩展到无穷大：

其中将t所在在域成为空间域，将u所在的予称为频率域
结论：空间域两个函数的卷积的傅里叶变换 = 两个函数傅里叶变换在频率域中在乘积
如果有两个函数傅里叶变换在乘积，那么我们可以通过计算傅里叶反变换而得到空间域卷积
f与F互为傅里叶变化对
相反的，如果有空间域中在两个函数在乘积我们可以通过傅里叶变换得到频率域卷积

3、图像频域中心化处理

用傅里叶变换的平移特性证明

其中

由傅里叶变换的平移特性可得

因此

去中心化处d理的原因：一张图像中的能量主要集中在低频区，中心化处理可以将图像的低频分量集中在频谱图中央，便于观察。
中心化：用（-1^x）乘以f(x)将位于原点在数据F(0)移动到【0，M-1】的中心位置。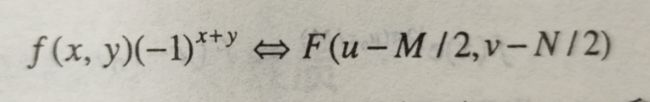

4.2二维离散傅里叶变换的一些性质

1、平移和旋转

用指数项乘以f(x,y)将使得DFT的原点移到（u0,v0）;反之，用负指数乘以F（u,v）将使f(x,y)的原点移到点（x0,y0）
平移不影响F(U,V)的幅度（谱）

旋转：F（u,v）旋转一个角度，则f(x,y)旋转相同在角度，反之亦然。

2.周期性

二维傅里叶变换和反变换在U和v方向是无限周期的。

中心化：用（-1^x）乘以f(x)将位于原点在数据F(0)移动到【0，M-1】的中心位置。

3、对称性

4、频率域滤波

低频对应图像中变化缓慢的灰度分量，对应着图像总体灰度级的显示
高频部分对应图像边缘和灰度级突变的部分，对应着图像中变化快在分量，图像的细节。
频率域滤波的步骤：

对于不同的滤波器，滤波函数H(u,v)不相同；
滤波器有陷波滤波器：除了原点有凹陷外，其他均是常量函数；，此滤波器可以设置F(0，0)为0，而保留其他傅里叶变换在频率成分不变。处理后的图像可以通过对H(u,v)*F(u,v)得到（将负值当0灰度级显示）

滤波在频率域中更加直观，在空间域中滤波器模板越小越好

4.3实现图像平滑的频率滤波器

由于边缘和其他尖锐变化（如噪声）在图像灰度级中主要处于傅里叶变化的高频部分，因此平滑（模糊）可以通过衰减指定图像傅里叶变化中高频成分的范围来实现。
频率域平滑滤波器有
1、理想低通滤波器

2、巴特沃思低通滤波器

3、高斯低通滤波器

√ 边缘和噪声等尖锐变化处于傅里叶变换的高 频部分

√ 平滑可以通过衰减高频成分的范围来实现

√ 理想低通滤波器：尖锐

√ 巴特沃思低通滤波器：处于理想和高斯滤波 器之间

√ 高斯低通滤波器：平滑

1.理想低通滤波器（ILPF）

在以原点为圆心，以D0为半径的圆内，无衰减的通过所有频率，而在该圆外切断所有频率的二维低通滤波器
理想低通滤波器是最简单的低通滤波器，是通过截断傅里叶变换中所有的高频成分，这些高频成分距离变换原点的距离比指定距离D0要远的多。
其变换函数是：



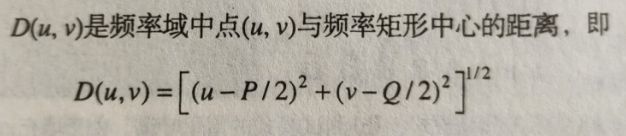
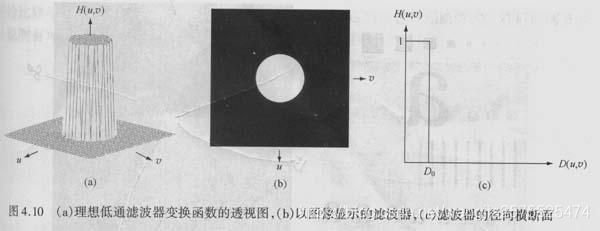
理想低通滤波器有振铃和模糊现象
理想低通滤波器在频率域的形状为矩形，那么其傅立叶逆变换在时间域为sinc函数；
图像处理中，对一幅图像进行滤波处理，若选用的频域滤波器具有陡峭的变化，则会使滤波图像产生“振铃”，所谓“振铃”，就是指输出图像的灰度剧烈变化处产生的震荡，就好像钟被敲击后产生的空气震荡

实现代码：

#include
#include

using namespace std;
using namespace cv;

//首先对图片定义一个函数，获取傅里叶最优尺寸大小，进而扩充图像边界，避免缠绕
cv::Mat image_make_border(cv::Mat &src)
{
	int w = getOptimalDFTSize(src.cols);//getOptimalDFTSize函数返回给定向量尺寸的傅里叶最优尺寸大小
	int h = getOptimalDFTSize(src.rows);
	Mat padded;
	copyMakeBorder(src, padded, 0, h - src.rows, 0, w - src.cols, BORDER_CONSTANT, Scalar::all(0));//该函数为边缘填充函数
	padded.convertTo(padded, CV_32FC1);
	return padded;
}
//第二定义一个频率域卷积的基本公式
Mat frequence_filter(Mat& src, Mat& blur)
{
	//先进行DFT傅里叶变换
	Mat plane[] = {  src, Mat::zeros(src.size() , CV_32FC1) };//创建通道，存储DFT后的实部与虚部（CV_32F，必须为单通道数）
	Mat complexIm;
	merge(plane, 2, complexIm);//合并通道 （把两个矩阵合并为一个2通道的Mat类容器）
	dft(complexIm, complexIm);//进行傅立叶变换，结果保存在自身
	//进行中心化操作
	split(complexIm, plane);//分离通道（数组分离）将原图数组分为0和1，黑的白的，分别对应实部和虚部
//    plane[0] = plane[0](Rect(0, 0, plane[0].cols & -2, plane[0].rows & -2));//这里为什么&上-2具体查看opencv文档
//    //其实是为了把行和列变成偶数 -2的二进制是11111111.......10 最后一位是0
	int cx = plane[0].cols / 2;
	int cy = plane[0].rows / 2;
	Mat part1_r(plane[0], Rect(0, 0, cx, cy)); //元素坐标表示为(cx,cy)
	Mat part2_r(plane[0], Rect(cx, 0, cx, cy));
	Mat part3_r(plane[0], Rect(0, cy, cx, cy));
	Mat part4_r(plane[0], Rect(cx, cy, cx, cy));
	
	Mat temp;
	part1_r.copyTo(temp); //左上与右下交换位置(实部)
	part4_r.copyTo(part1_r);
	temp.copyTo(part4_r);

	part2_r.copyTo(temp);//右上与左下交换位置(实部)
	part3_r.copyTo(part2_r);
	temp.copyTo(part3_r);
	
	Mat part1_i(plane[1], Rect(0, 0, cx, cy)); //元素坐标(cx,cy)
	Mat part2_i(plane[1], Rect(cx, 0, cx, cy));
	Mat part3_i(plane[1], Rect(0, cy, cx, cy));
	Mat part4_i(plane[1], Rect(cx, cy, cx, cy));
	
	part1_i.copyTo(temp); //左上与右下交换位置(虚部)
	part4_i.copyTo(part1_i);
	temp.copyTo(part4_i);

	part2_i.copyTo(temp); //右上与左下交换位置(虚部)
	part3_i.copyTo(part2_i);
	temp.copyTo(part3_i);

	//第三步是滤波器函数和DFT结果相乘
	Mat blur_r, blur_i, BLUR;
	multiply(plane[0], blur, blur_r); //滤波（实部与滤波器模板对应元素相乘）
	multiply(plane[1], blur, blur_i);//滤波（虚部与滤波器模板对应元素相乘）
	Mat plane1[] = { blur_r, blur_i };
	merge(plane1, 2, BLUR);//实部与虚部合并


	//最后得到原图频谱图
	magnitude(plane[0], plane[1], plane[0]);//获取幅度图像，0通道为实部通道，1为虚部，因为二维傅立叶变换结果是复数
	plane[0] += Scalar::all(1);//傅立叶变换后的图片不好分析，进行对数处理，结果比较好看
	log(plane[0], plane[0]);// float型的灰度空间为[0，1])
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX);//归一化便于显示

	idft(BLUR, BLUR);//idft二维傅里叶变化的结果也为复数
	split(BLUR, plane);//分离通道，主要获取通道
	magnitude(plane[0], plane[1], plane[0]); //求幅值(模)
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX); //归一化便于显示
	return plane[0];//返回参数
	
}


//定义理想低通滤波器函数
Mat ideal_low_kernel(Mat&src, float sigma)
{
	Mat ideal_low_pass(src.size(), CV_32FC1);
	float d0 = sigma;//半径D0越小，模糊越大；半径D0越大，模糊越小
	for (int i = 0; i < src.rows; i++)
	{
		for (int j = 0; j < src.cols; j++)
		{
			double d = sqrt(pow((i - src.rows / 2), 2) + pow((j - src.cols / 2), 2));//分子,计算pow必须为float型
			if (d <= d0)
			{
				ideal_low_pass.at<float>(i, j) = 1;
			}
			else
			{
				ideal_low_pass.at<float>(i, j) = 0;
			}
		}
	}
	//显示滤波器
	string name = "理想低通滤波器=" + std::to_string(sigma);//std::to_string将数值转化为字符串。返回对应的字符串。
	cv::imshow(name, ideal_low_pass);
	return ideal_low_pass;
}
cv::Mat ideal_low_pass_filter(Mat &src, float sigma)
{
	Mat padded = image_make_border(src);
	Mat ideal_kernel = ideal_low_kernel(padded, sigma);
	Mat result = frequence_filter(padded, ideal_kernel);
	return result;
}
int main()
{
	Mat img = imread("C:/Users/征途/Desktop/vs-cpp/第四章/01.jpg", IMREAD_GRAYSCALE);
	cv::Mat ideal = ideal_low_pass_filter(img, 10.00000);
	ideal = ideal(cv::Rect(0, 0, img.cols, img.rows));
	imshow("img",ideal);
	waitKey(0);
	return 0;
}

D0=10时结果：

2.巴特沃斯低通滤波器（BLPF）

截止频率位于距原点D0处的n阶巴特沃斯低通滤波器（BLPF）的传递函数为：

与理想滤波器不同的是，BLPF传递函数并没有给出明显截止的尖锐的不连续性。
在上式中，截止频率点是当D(u，v)=D0时的点【即H(u，v)从其最大值下降为50%】
空间域的一阶巴特沃斯滤波器没有振铃现象，在二阶滤波器中，振铃现象通常很难察觉，只有更高阶数才能显示明显的振铃现象。
//巴特沃斯低通滤波器

#include
#include

using namespace std;
using namespace cv;

//首先对图片定义一个函数，获取傅里叶最优尺寸大小，进而扩充图像边界，避免缠绕
cv::Mat image_make_border(cv::Mat &src)
{
	int w = getOptimalDFTSize(src.cols);//getOptimalDFTSize函数返回给定向量尺寸的傅里叶最优尺寸大小
	int h = getOptimalDFTSize(src.rows);
	Mat padded;
	copyMakeBorder(src, padded, 0, h - src.rows, 0, w - src.cols, BORDER_CONSTANT, Scalar::all(0));//该函数为边缘填充函数
	padded.convertTo(padded, CV_32FC1);
	return padded;
}
//第二定义一个频率域卷积的基本公式
Mat frequence_filter(Mat& src, Mat& blur)
{
	//先进行DFT傅里叶变换
	Mat plane[] = {  src, Mat::zeros(src.size() , CV_32FC1) };//创建通道，存储DFT后的实部与虚部（CV_32F，必须为单通道数）
	Mat complexIm;
	merge(plane, 2, complexIm);//合并通道 （把两个矩阵合并为一个2通道的Mat类容器）
	dft(complexIm, complexIm);//进行傅立叶变换，结果保存在自身
	//进行中心化操作
	split(complexIm, plane);//分离通道（数组分离）将原图数组分为0和1，黑的白的，分别对应实部和虚部
//    plane[0] = plane[0](Rect(0, 0, plane[0].cols & -2, plane[0].rows & -2));//这里为什么&上-2具体查看opencv文档
//    //其实是为了把行和列变成偶数 -2的二进制是11111111.......10 最后一位是0
	int cx = plane[0].cols / 2;
	int cy = plane[0].rows / 2;
	Mat part1_r(plane[0], Rect(0, 0, cx, cy)); //元素坐标表示为(cx,cy)
	Mat part2_r(plane[0], Rect(cx, 0, cx, cy));
	Mat part3_r(plane[0], Rect(0, cy, cx, cy));
	Mat part4_r(plane[0], Rect(cx, cy, cx, cy));
	
	Mat temp;
	part1_r.copyTo(temp); //左上与右下交换位置(实部)
	part4_r.copyTo(part1_r);
	temp.copyTo(part4_r);

	part2_r.copyTo(temp);//右上与左下交换位置(实部)
	part3_r.copyTo(part2_r);
	temp.copyTo(part3_r);
	
	Mat part1_i(plane[1], Rect(0, 0, cx, cy)); //元素坐标(cx,cy)
	Mat part2_i(plane[1], Rect(cx, 0, cx, cy));
	Mat part3_i(plane[1], Rect(0, cy, cx, cy));
	Mat part4_i(plane[1], Rect(cx, cy, cx, cy));
	
	part1_i.copyTo(temp); //左上与右下交换位置(虚部)
	part4_i.copyTo(part1_i);
	temp.copyTo(part4_i);

	part2_i.copyTo(temp); //右上与左下交换位置(虚部)
	part3_i.copyTo(part2_i);
	temp.copyTo(part3_i);

	//第三步是滤波器函数和DFT结果相乘
	Mat blur_r, blur_i, BLUR;
	multiply(plane[0], blur, blur_r); //滤波（实部与滤波器模板对应元素相乘）
	multiply(plane[1], blur, blur_i);//滤波（虚部与滤波器模板对应元素相乘）
	Mat plane1[] = { blur_r, blur_i };
	merge(plane1, 2, BLUR);//实部与虚部合并


	//最后得到原图频谱图
	magnitude(plane[0], plane[1], plane[0]);//获取幅度图像，0通道为实部通道，1为虚部，因为二维傅立叶变换结果是复数
	plane[0] += Scalar::all(1);//傅立叶变换后的图片不好分析，进行对数处理，结果比较好看
	log(plane[0], plane[0]);// float型的灰度空间为[0，1])
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX);//归一化便于显示

	idft(BLUR, BLUR);//idft二维傅里叶变化的结果也为复数
	split(BLUR, plane);//分离通道，主要获取通道
	magnitude(plane[0], plane[1], plane[0]); //求幅值(模)
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX); //归一化便于显示
	return plane[0];//返回参数
	
}
Mat butterworth_low_kernel(Mat &scr, float sigma, int n)//n是阶数
{
	Mat butterworth_low_pass(scr.size(), CV_32FC1); //，CV_32FC1
	double D0 = sigma;//半径D0越小，模糊越大；半径D0越大，模糊越小
	for(int i = 0; i < scr.rows; i++)
	{
		for (int j = 0; j < scr.cols; i++)
		{
			//下面两行是应用巴特沃斯的公式
			double d = sqrt(pow((i - scr.rows / 2), 2) + pow((j - scr.cols / 2), 2));//分子,计算pow必须为float型
			butterworth_low_pass.at<float>(i, j) = 1.0 / (1 + pow(d/D0, 2 * n));
		}
	}
	string name = "巴特沃斯低通滤波器d0=" + std::to_string(sigma) + "n=" + std::to_string(n);
	imshow(name, butterworth_low_pass);
	return butterworth_low_pass;
}
//巴特沃斯函数封装
Mat butterworth_low_paass_filter(Mat &src, float d0, int n)
{
	//H = 1 / (1+(D/D0)^2n)    n表示巴特沃斯滤波器的次数
   //阶数n=1 无振铃和负值    阶数n=2 轻微振铃和负值  阶数n=5 明显振铃和负值   阶数n=20 与ILPF相似
	Mat padded = image_make_border(src);
	Mat butterworth_kernel = butterworth_low_kernel(padded, d0, n);
	Mat result = frequence_filter(padded, butterworth_kernel);
	return result;
}

3.高斯低通滤波器GLPF

高斯滤波器没有振铃现象，且边缘平滑，传递函数为：其中D0是截止频率，当D=D0时，GLPF下降到其最大值的0.607处。

#include
#include

using namespace std;
using namespace cv;

//首先对图片定义一个函数，获取傅里叶最优尺寸大小，进而扩充图像边界，避免缠绕
cv::Mat image_make_border(cv::Mat &src)
{
	int w = getOptimalDFTSize(src.cols);//getOptimalDFTSize函数返回给定向量尺寸的傅里叶最优尺寸大小
	int h = getOptimalDFTSize(src.rows);
	Mat padded;
	copyMakeBorder(src, padded, 0, h - src.rows, 0, w - src.cols, BORDER_CONSTANT, Scalar::all(0));//该函数为边缘填充函数
	padded.convertTo(padded, CV_32FC1);
	return padded;
}
//第二定义一个频率域卷积的基本公式
Mat frequence_filter(Mat& src, Mat& blur)
{
	//先进行DFT傅里叶变换
	Mat plane[] = {  src, Mat::zeros(src.size() , CV_32FC1) };//创建通道，存储DFT后的实部与虚部（CV_32F，必须为单通道数）
	Mat complexIm;
	merge(plane, 2, complexIm);//合并通道 （把两个矩阵合并为一个2通道的Mat类容器）
	dft(complexIm, complexIm);//进行傅立叶变换，结果保存在自身
	//进行中心化操作
	split(complexIm, plane);//分离通道（数组分离）将原图数组分为0和1，黑的白的，分别对应实部和虚部
//    plane[0] = plane[0](Rect(0, 0, plane[0].cols & -2, plane[0].rows & -2));//这里为什么&上-2具体查看opencv文档
//    //其实是为了把行和列变成偶数 -2的二进制是11111111.......10 最后一位是0
	int cx = plane[0].cols / 2;
	int cy = plane[0].rows / 2;
	Mat part1_r(plane[0], Rect(0, 0, cx, cy)); //元素坐标表示为(cx,cy)
	Mat part2_r(plane[0], Rect(cx, 0, cx, cy));
	Mat part3_r(plane[0], Rect(0, cy, cx, cy));
	Mat part4_r(plane[0], Rect(cx, cy, cx, cy));
	
	Mat temp;
	part1_r.copyTo(temp); //左上与右下交换位置(实部)
	part4_r.copyTo(part1_r);
	temp.copyTo(part4_r);

	part2_r.copyTo(temp);//右上与左下交换位置(实部)
	part3_r.copyTo(part2_r);
	temp.copyTo(part3_r);
	
	Mat part1_i(plane[1], Rect(0, 0, cx, cy)); //元素坐标(cx,cy)
	Mat part2_i(plane[1], Rect(cx, 0, cx, cy));
	Mat part3_i(plane[1], Rect(0, cy, cx, cy));
	Mat part4_i(plane[1], Rect(cx, cy, cx, cy));
	
	part1_i.copyTo(temp); //左上与右下交换位置(虚部)
	part4_i.copyTo(part1_i);
	temp.copyTo(part4_i);

	part2_i.copyTo(temp); //右上与左下交换位置(虚部)
	part3_i.copyTo(part2_i);
	temp.copyTo(part3_i);

	//第三步是滤波器函数和DFT结果相乘
	Mat blur_r, blur_i, BLUR;
	multiply(plane[0], blur, blur_r); //滤波（实部与滤波器模板对应元素相乘）
	multiply(plane[1], blur, blur_i);//滤波（虚部与滤波器模板对应元素相乘）
	Mat plane1[] = { blur_r, blur_i };
	merge(plane1, 2, BLUR);//实部与虚部合并


	//最后得到原图频谱图
	magnitude(plane[0], plane[1], plane[0]);//获取幅度图像，0通道为实部通道，1为虚部，因为二维傅立叶变换结果是复数
	plane[0] += Scalar::all(1);//傅立叶变换后的图片不好分析，进行对数处理，结果比较好看
	log(plane[0], plane[0]);// float型的灰度空间为[0，1])
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX);//归一化便于显示

	idft(BLUR, BLUR);//idft二维傅里叶变化的结果也为复数
	split(BLUR, plane);//分离通道，主要获取通道
	magnitude(plane[0], plane[1], plane[0]); //求幅值(模)
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX); //归一化便于显示
	return plane[0];//返回参数	
}
//高斯低通滤波器
Mat gaussian_low_pass_kernel(Mat scr, float sigma)
{
	Mat gaussianBlur(scr.size(), CV_32FC1); //，CV_32FC1
	float d0 = 2 * sigma*sigma;//高斯函数参数，越小，频率高斯滤波器越窄，滤除高频成分越多，图像就越平滑
	for (int i = 0; i < scr.rows; i++) {
		for (int j = 0; j < scr.cols; j++) {
			float d = pow(float(i - scr.rows / 2), 2) + pow(float(j - scr.cols / 2), 2);//分子,计算pow必须为float型
			gaussianBlur.at<float>(i, j) = expf(-d / d0);//expf为以e为底求幂（必须为float型）
		}
	}
	string name = "高斯低通滤波器d0=" + std::to_string(sigma);
	imshow(name, gaussianBlur);
	return gaussianBlur;
}
Mat gaussian_low_pass_filter(Mat &src, float d0)
{
	Mat padded = image_make_border(src);
	Mat gaussian_kernel = gaussian_low_pass_kernel(padded, d0);//理想低通滤波器
	Mat result = frequence_filter(padded, gaussian_kernel);
	return result;
}
int main()
{
	Mat img = imread("C:/Users/征途/Desktop/vs-cpp/第四章/01.jpg", IMREAD_GRAYSCALE);
	cv::Mat ideal = gaussian_low_pass_filter(img, 160);
	ideal = ideal(cv::Rect(0, 0, img.cols, img.rows));
	imshow("img",ideal);
	waitKey(0);
	return 0;

}

D0=160时结果

4.4使用频率域滤波器锐化图像

高通滤波衰减傅里叶变换中的低频分量而不影响高频分量。
理想高通滤波器：锐利性大
巴特沃斯高通滤波器：介于上下两者之间，属于过渡
高斯高通滤波器：宽阔平滑性大

4.4.1理想高通滤波器(二维IHPF)

二维理想高通滤波器与理想低通滤波器相对，传递函数为：

IHPF是将以D0为半径的圆内的所有频率置零，而毫无衰减的通过圆外所有频率。和理想低通一样IHPF在物理上是不可实现的。
IHPF的振铃现象很严重，导致失真。
所有图像的恒定背景在高通滤波后的图像中都是0，因此高通滤波类似于空间域的差分。


实现代码：

#include
#include
#include

using namespace std;
using namespace cv;

//首先对图片定义一个函数，获取傅里叶最优尺寸大小，进而扩充图像边界，避免缠绕
cv::Mat image_make_border(cv::Mat &src)
{
	int w = getOptimalDFTSize(src.cols);//getOptimalDFTSize函数返回给定向量尺寸的傅里叶最优尺寸大小
	int h = getOptimalDFTSize(src.rows);
	Mat padded;
	copyMakeBorder(src, padded, 0, h - src.rows, 0, w - src.cols, BORDER_CONSTANT, Scalar::all(0));//该函数为边缘填充函数
	padded.convertTo(padded, CV_32FC1);
	return padded;
}
//第二定义一个频率域卷积的基本公式
Mat frequence_filter(Mat& src, Mat& blur)
{
	//先进行DFT傅里叶变换
	Mat plane[] = { src, Mat::zeros(src.size() , CV_32FC1) };//创建通道，存储DFT后的实部与虚部（CV_32F，必须为单通道数）
	Mat complexIm;
	merge(plane, 2, complexIm);//合并通道 （把两个矩阵合并为一个2通道的Mat类容器）
	dft(complexIm, complexIm);//进行傅立叶变换，结果保存在自身
	//进行中心化操作
	split(complexIm, plane);//分离通道（数组分离）将原图数组分为0和1，黑的白的，分别对应实部和虚部
//    plane[0] = plane[0](Rect(0, 0, plane[0].cols & -2, plane[0].rows & -2));//这里为什么&上-2具体查看opencv文档
//    //其实是为了把行和列变成偶数 -2的二进制是11111111.......10 最后一位是0
	int cx = plane[0].cols / 2;
	int cy = plane[0].rows / 2;
	Mat part1_r(plane[0], Rect(0, 0, cx, cy)); //元素坐标表示为(cx,cy)
	Mat part2_r(plane[0], Rect(cx, 0, cx, cy));
	Mat part3_r(plane[0], Rect(0, cy, cx, cy));
	Mat part4_r(plane[0], Rect(cx, cy, cx, cy));

	Mat temp;
	part1_r.copyTo(temp); //左上与右下交换位置(实部)
	part4_r.copyTo(part1_r);
	temp.copyTo(part4_r);

	part2_r.copyTo(temp);//右上与左下交换位置(实部)
	part3_r.copyTo(part2_r);
	temp.copyTo(part3_r);

	Mat part1_i(plane[1], Rect(0, 0, cx, cy)); //元素坐标(cx,cy)
	Mat part2_i(plane[1], Rect(cx, 0, cx, cy));
	Mat part3_i(plane[1], Rect(0, cy, cx, cy));
	Mat part4_i(plane[1], Rect(cx, cy, cx, cy));

	part1_i.copyTo(temp); //左上与右下交换位置(虚部)
	part4_i.copyTo(part1_i);
	temp.copyTo(part4_i);

	part2_i.copyTo(temp); //右上与左下交换位置(虚部)
	part3_i.copyTo(part2_i);
	temp.copyTo(part3_i);

	//第三步是滤波器函数和DFT结果相乘
	Mat blur_r, blur_i, BLUR;
	multiply(plane[0], blur, blur_r); //滤波（实部与滤波器模板对应元素相乘）
	multiply(plane[1], blur, blur_i);//滤波（虚部与滤波器模板对应元素相乘）
	Mat plane1[] = { blur_r, blur_i };
	merge(plane1, 2, BLUR);//实部与虚部合并


	//最后得到原图频谱图
	magnitude(plane[0], plane[1], plane[0]);//获取幅度图像，0通道为实部通道，1为虚部，因为二维傅立叶变换结果是复数
	plane[0] += Scalar::all(1);//傅立叶变换后的图片不好分析，进行对数处理，结果比较好看
	log(plane[0], plane[0]);// float型的灰度空间为[0，1])
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX);//归一化便于显示

	idft(BLUR, BLUR);//idft二维傅里叶变化的结果也为复数
	split(BLUR, plane);//分离通道，主要获取通道
	magnitude(plane[0], plane[1], plane[0]); //求幅值(模)
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX); //归一化便于显示
	return plane[0];//返回参数

}
//理想高通滤波器传递函数的实现
Mat ideal_high_kernel(Mat &src, float sigma)
{
	Mat ideal_high_pass(src.size(), CV_32FC1);
	float d0 = sigma;//半径D0越小，模糊越大；半径D0越大，模糊越小
	for (int i = 0; i < src.rows; i++)
	{
		for (int j = 0; j < src.cols; j++)
		{
			double d = sqrt(pow((i - src.rows / 2), 2) + pow((j - src.cols / 2), 2));
			if (d <= d0)
			{
				ideal_high_pass.at<float>(i, j) = 0;
			}
			else
			{
				ideal_high_pass.at<float>(i, j) = 1;
			}
		}
	}
	string name = "理想高通滤波器d0=" + std::to_string(sigma);
	imshow(name, ideal_high_pass);
	return ideal_high_pass;
}
//对理想高通滤波器函数进行封装
cv::Mat ideal_high_pass_filter(Mat &src, float sigma)
{
	Mat padded = image_make_border(src);
	Mat ideal_kernel = ideal_high_kernel(padded, sigma);
	Mat result = frequence_filter(padded, ideal_kernel);
	return result;
}
int main()
{
	Mat img = imread("C:/Users/征途/Desktop/vs-cpp/第四章/01.jpg", IMREAD_GRAYSCALE);
	cv::Mat ideal = ideal_high_pass_filter(img, 160);
	ideal = ideal(cv::Rect(0, 0, img.cols, img.rows));
	imshow("img", ideal);
	waitKey(0);
	return 0;

}

D0=160的结果：

4.4.2巴特沃斯高通滤波器BHPF

截止频率为D0的n阶巴特沃斯高通滤波器定义为：

其中D(u，v)：

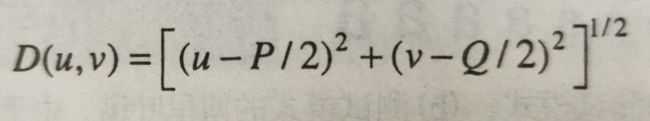
截止频率越大，使用BHPF得到的结果越平滑

#include
#include
#include

using namespace std;
using namespace cv;

//首先对图片定义一个函数，获取傅里叶最优尺寸大小，进而扩充图像边界，避免缠绕
cv::Mat image_make_border(cv::Mat &src)
{
	int w = getOptimalDFTSize(src.cols);//getOptimalDFTSize函数返回给定向量尺寸的傅里叶最优尺寸大小
	int h = getOptimalDFTSize(src.rows);
	Mat padded;
	copyMakeBorder(src, padded, 0, h - src.rows, 0, w - src.cols, BORDER_CONSTANT, Scalar::all(0));//该函数为边缘填充函数
	padded.convertTo(padded, CV_32FC1);
	return padded;
}
//第二定义一个频率域卷积的基本公式
Mat frequence_filter(Mat& src, Mat& blur)
{
	//先进行DFT傅里叶变换
	Mat plane[] = { src, Mat::zeros(src.size() , CV_32FC1) };//创建通道，存储DFT后的实部与虚部（CV_32F，必须为单通道数）
	Mat complexIm;
	merge(plane, 2, complexIm);//合并通道 （把两个矩阵合并为一个2通道的Mat类容器）
	dft(complexIm, complexIm);//进行傅立叶变换，结果保存在自身
	//进行中心化操作
	split(complexIm, plane);//分离通道（数组分离）将原图数组分为0和1，黑的白的，分别对应实部和虚部
//    plane[0] = plane[0](Rect(0, 0, plane[0].cols & -2, plane[0].rows & -2));//这里为什么&上-2具体查看opencv文档
//    //其实是为了把行和列变成偶数 -2的二进制是11111111.......10 最后一位是0
	int cx = plane[0].cols / 2;
	int cy = plane[0].rows / 2;
	Mat part1_r(plane[0], Rect(0, 0, cx, cy)); //元素坐标表示为(cx,cy)
	Mat part2_r(plane[0], Rect(cx, 0, cx, cy));
	Mat part3_r(plane[0], Rect(0, cy, cx, cy));
	Mat part4_r(plane[0], Rect(cx, cy, cx, cy));

	Mat temp;
	part1_r.copyTo(temp); //左上与右下交换位置(实部)
	part4_r.copyTo(part1_r);
	temp.copyTo(part4_r);

	part2_r.copyTo(temp);//右上与左下交换位置(实部)
	part3_r.copyTo(part2_r);
	temp.copyTo(part3_r);

	Mat part1_i(plane[1], Rect(0, 0, cx, cy)); //元素坐标(cx,cy)
	Mat part2_i(plane[1], Rect(cx, 0, cx, cy));
	Mat part3_i(plane[1], Rect(0, cy, cx, cy));
	Mat part4_i(plane[1], Rect(cx, cy, cx, cy));

	part1_i.copyTo(temp); //左上与右下交换位置(虚部)
	part4_i.copyTo(part1_i);
	temp.copyTo(part4_i);

	part2_i.copyTo(temp); //右上与左下交换位置(虚部)
	part3_i.copyTo(part2_i);
	temp.copyTo(part3_i);

	//第三步是滤波器函数和DFT结果相乘
	Mat blur_r, blur_i, BLUR;
	multiply(plane[0], blur, blur_r); //滤波（实部与滤波器模板对应元素相乘）
	multiply(plane[1], blur, blur_i);//滤波（虚部与滤波器模板对应元素相乘）
	Mat plane1[] = { blur_r, blur_i };
	merge(plane1, 2, BLUR);//实部与虚部合并


	//最后得到原图频谱图
	magnitude(plane[0], plane[1], plane[0]);//获取幅度图像，0通道为实部通道，1为虚部，因为二维傅立叶变换结果是复数
	plane[0] += Scalar::all(1);//傅立叶变换后的图片不好分析，进行对数处理，结果比较好看
	log(plane[0], plane[0]);// float型的灰度空间为[0，1])
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX);//归一化便于显示

	idft(BLUR, BLUR);//idft二维傅里叶变化的结果也为复数
	split(BLUR, plane);//分离通道，主要获取通道
	magnitude(plane[0], plane[1], plane[0]); //求幅值(模)
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX); //归一化便于显示
	return plane[0];//返回参数

}
//巴特沃斯高通滤波器
cv::Mat butterworth_high_kernel(Mat &src, float sigma, int n)
{
	Mat butterworth_high_pass(src.size(), CV_32FC1);
	double d0 = sigma;//半径D0越小，模糊越大；半径D0越大，模糊越小
	for (int i = 0; i < src.rows; i++)
	{
		for (int j = 0; j < src.cols; j++)
		{
			double d = sqrt(pow((i - src.rows / 2), 2) + pow((j - src.cols / 2), 2));
			butterworth_high_pass.at<float>(i, j) = 1.0 / (1 + pow(d0 / d, 2 * n));
		}
	}
	string name = "巴特沃斯高通滤波器d0=" + std::to_string(sigma) + "n = " + std::to_string(n);
	imshow(name, butterworth_high_pass);
	return butterworth_high_pass;
}
//巴特沃斯高通滤波器封装
Mat butterworth_high_pass_filter(Mat &src, float d0, int n)
{
	// H = 1 / (1 + (D0 / D) ^ 2n)    n表示巴特沃斯滤波器的次数
	Mat padded = image_make_border(src);
	Mat butterworth_kernel = butterworth_high_kernel(padded, d0, n);
	Mat result = frequence_filter(padded, butterworth_kernel);
	return result;
}
int main()
{
	Mat img = imread("C:/Users/征途/Desktop/vs-cpp/第四章/01.jpg", IMREAD_GRAYSCALE);
	cv::Mat ideal2 = butterworth_high_pass_filter(img, 160,2);
	ideal2 = ideal2(cv::Rect(0, 0, img.cols, img.rows));
	imshow("img", ideal2);
	waitKey(0);
	return 0;

}

结果显示：

4.4.3高斯高通滤波器GHPF

对微小物体和细线条采用高斯滤波，结果也比较清晰
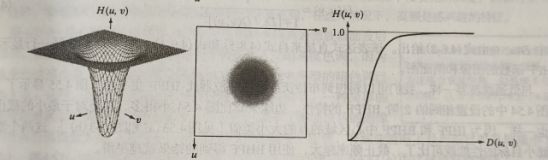
截止频率处在距频率矩形中心距离为D0的高斯高通滤波器传递函数：

#include
#include
#include

using namespace std;
using namespace cv;

//首先对图片定义一个函数，获取傅里叶最优尺寸大小，进而扩充图像边界，避免缠绕
cv::Mat image_make_border(cv::Mat &src)
{
	int w = getOptimalDFTSize(src.cols);//getOptimalDFTSize函数返回给定向量尺寸的傅里叶最优尺寸大小
	int h = getOptimalDFTSize(src.rows);
	Mat padded;
	copyMakeBorder(src, padded, 0, h - src.rows, 0, w - src.cols, BORDER_CONSTANT, Scalar::all(0));//该函数为边缘填充函数
	padded.convertTo(padded, CV_32FC1);
	return padded;
}
//第二定义一个频率域卷积的基本公式
Mat frequence_filter(Mat& src, Mat& blur)
{
	//先进行DFT傅里叶变换
	Mat plane[] = { src, Mat::zeros(src.size() , CV_32FC1) };//创建通道，存储DFT后的实部与虚部（CV_32F，必须为单通道数）
	Mat complexIm;
	merge(plane, 2, complexIm);//合并通道 （把两个矩阵合并为一个2通道的Mat类容器）
	dft(complexIm, complexIm);//进行傅立叶变换，结果保存在自身
	//进行中心化操作
	split(complexIm, plane);//分离通道（数组分离）将原图数组分为0和1，黑的白的，分别对应实部和虚部
//    plane[0] = plane[0](Rect(0, 0, plane[0].cols & -2, plane[0].rows & -2));//这里为什么&上-2具体查看opencv文档
//    //其实是为了把行和列变成偶数 -2的二进制是11111111.......10 最后一位是0
	int cx = plane[0].cols / 2;
	int cy = plane[0].rows / 2;
	Mat part1_r(plane[0], Rect(0, 0, cx, cy)); //元素坐标表示为(cx,cy)
	Mat part2_r(plane[0], Rect(cx, 0, cx, cy));
	Mat part3_r(plane[0], Rect(0, cy, cx, cy));
	Mat part4_r(plane[0], Rect(cx, cy, cx, cy));

	Mat temp;
	part1_r.copyTo(temp); //左上与右下交换位置(实部)
	part4_r.copyTo(part1_r);
	temp.copyTo(part4_r);

	part2_r.copyTo(temp);//右上与左下交换位置(实部)
	part3_r.copyTo(part2_r);
	temp.copyTo(part3_r);

	Mat part1_i(plane[1], Rect(0, 0, cx, cy)); //元素坐标(cx,cy)
	Mat part2_i(plane[1], Rect(cx, 0, cx, cy));
	Mat part3_i(plane[1], Rect(0, cy, cx, cy));
	Mat part4_i(plane[1], Rect(cx, cy, cx, cy));

	part1_i.copyTo(temp); //左上与右下交换位置(虚部)
	part4_i.copyTo(part1_i);
	temp.copyTo(part4_i);

	part2_i.copyTo(temp); //右上与左下交换位置(虚部)
	part3_i.copyTo(part2_i);
	temp.copyTo(part3_i);

	//第三步是滤波器函数和DFT结果相乘
	Mat blur_r, blur_i, BLUR;
	multiply(plane[0], blur, blur_r); //滤波（实部与滤波器模板对应元素相乘）
	multiply(plane[1], blur, blur_i);//滤波（虚部与滤波器模板对应元素相乘）
	Mat plane1[] = { blur_r, blur_i };
	merge(plane1, 2, BLUR);//实部与虚部合并


	//最后得到原图频谱图
	magnitude(plane[0], plane[1], plane[0]);//获取幅度图像，0通道为实部通道，1为虚部，因为二维傅立叶变换结果是复数
	plane[0] += Scalar::all(1);//傅立叶变换后的图片不好分析，进行对数处理，结果比较好看
	log(plane[0], plane[0]);// float型的灰度空间为[0，1])
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX);//归一化便于显示

	idft(BLUR, BLUR);//idft二维傅里叶变化的结果也为复数
	split(BLUR, plane);//分离通道，主要获取通道
	magnitude(plane[0], plane[1], plane[0]); //求幅值(模)
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX); //归一化便于显示
	return plane[0];//返回参数
}
//高斯高通滤波器传递函数
Mat gaussian_high_pass_kernel(Mat &src, float sigma)
{
	Mat gaussianBlur(src.size(), CV_32FC1);
	float d0 = 2 * sigma*sigma;//高斯函数参数，越小，频率高斯滤波器越窄，滤除高频成分越多，图像就越平滑
	for (int i = 0; i < src.rows; i++)
	{
		for (int j = 0; j < src.cols; j++)
		{
			float d = sqrt(pow(float(i - src.rows / 2), 2) + pow(float(j - src.cols / 2), 2));
			gaussianBlur.at<float>(i, j) = 1 - expf(-pow(d,2) /2*pow(d0,2));

		}
	}
	string name = "高斯高通滤波器d0=" + std::to_string(sigma);
	imshow(name,gaussianBlur);
	return gaussianBlur;
}
//高斯高通滤波器封装
Mat gaussian_high_pass_filter(Mat &src, float d0)
{
	Mat padded = image_make_border(src);
	Mat gaussian_kernel = gaussian_high_pass_kernel(padded, d0);//理想低通滤波器
	Mat result = frequence_filter(padded, gaussian_kernel);
	return result;

}

int main()
{
	Mat img = imread("C:/Users/征途/Desktop/vs-cpp/第四章/01.jpg", IMREAD_GRAYSCALE);
	cv::Mat ideal3 = gaussian_high_pass_filter(img, 160);
	ideal3 = ideal3(cv::Rect(0, 0, img.cols, img.rows));
	imshow("img3", ideal3);
	waitKey(0);
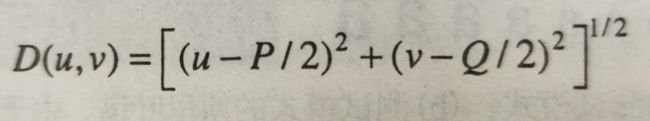
	return 0;
}

4.4.4频率域中的拉普拉斯算子

首先是拉普拉斯在频率域中使用的滤波器模板如下：

或者采用下面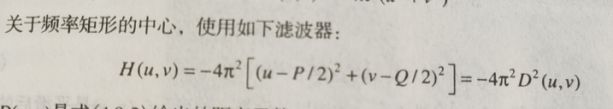

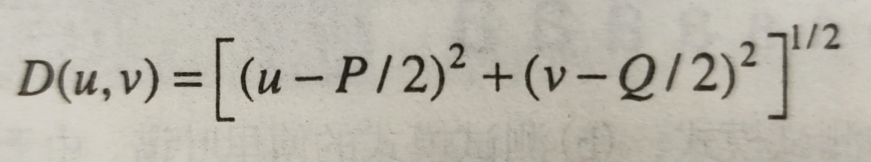
然后计算拉普拉斯算子图像（F(U,V）是f的傅里叶变换：

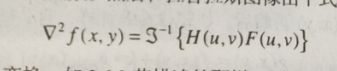
最后与源图像叠加，实现源图像的增强：

在频率域中上述式子可写成：

#include
#include
#include

using namespace std;
using namespace cv;

//首先对图片定义一个函数，获取傅里叶最优尺寸大小，进而扩充图像边界，避免缠绕
cv::Mat image_make_border(cv::Mat &src)
{
	int w = getOptimalDFTSize(src.cols);//getOptimalDFTSize函数返回给定向量尺寸的傅里叶最优尺寸大小
	int h = getOptimalDFTSize(src.rows);
	Mat padded;
	copyMakeBorder(src, padded, 0, h - src.rows, 0, w - src.cols, BORDER_CONSTANT, Scalar::all(0));//该函数为边缘填充函数
	padded.convertTo(padded, CV_32FC1);
	return padded;
}
//第二定义一个频率域卷积的基本公式
Mat frequence_filter(Mat& src, Mat& blur)
{
	//先进行DFT傅里叶变换
	Mat plane[] = { src, Mat::zeros(src.size() , CV_32FC1) };//创建通道，存储DFT后的实部与虚部（CV_32F，必须为单通道数）
	Mat complexIm;
	merge(plane, 2, complexIm);//合并通道 （把两个矩阵合并为一个2通道的Mat类容器）
	dft(complexIm, complexIm);//进行傅立叶变换，结果保存在自身
	//进行中心化操作
	split(complexIm, plane);//分离通道（数组分离）将原图数组分为0和1，黑的白的，分别对应实部和虚部
//    plane[0] = plane[0](Rect(0, 0, plane[0].cols & -2, plane[0].rows & -2));//这里为什么&上-2具体查看opencv文档
//    //其实是为了把行和列变成偶数 -2的二进制是11111111.......10 最后一位是0
	int cx = plane[0].cols / 2;
	int cy = plane[0].rows / 2;
	Mat part1_r(plane[0], Rect(0, 0, cx, cy)); //元素坐标表示为(cx,cy)
	Mat part2_r(plane[0], Rect(cx, 0, cx, cy));
	Mat part3_r(plane[0], Rect(0, cy, cx, cy));
	Mat part4_r(plane[0], Rect(cx, cy, cx, cy));

	Mat temp;
	part1_r.copyTo(temp); //左上与右下交换位置(实部)
	part4_r.copyTo(part1_r);
	temp.copyTo(part4_r);

	part2_r.copyTo(temp);//右上与左下交换位置(实部)
	part3_r.copyTo(part2_r);
	temp.copyTo(part3_r);

	Mat part1_i(plane[1], Rect(0, 0, cx, cy)); //元素坐标(cx,cy)
	Mat part2_i(plane[1], Rect(cx, 0, cx, cy));
	Mat part3_i(plane[1], Rect(0, cy, cx, cy));
	Mat part4_i(plane[1], Rect(cx, cy, cx, cy));

	part1_i.copyTo(temp); //左上与右下交换位置(虚部)
	part4_i.copyTo(part1_i);
	temp.copyTo(part4_i);

	part2_i.copyTo(temp); //右上与左下交换位置(虚部)
	part3_i.copyTo(part2_i);
	temp.copyTo(part3_i);

	//第三步是滤波器函数和DFT结果相乘
	Mat blur_r, blur_i, BLUR;
	multiply(plane[0], blur, blur_r); //滤波（实部与滤波器模板对应元素相乘）
	multiply(plane[1], blur, blur_i);//滤波（虚部与滤波器模板对应元素相乘）
	Mat plane1[] = { blur_r, blur_i };
	merge(plane1, 2, BLUR);//实部与虚部合并


	//最后得到原图频谱图
	magnitude(plane[0], plane[1], plane[0]);//获取幅度图像，0通道为实部通道，1为虚部，因为二维傅立叶变换结果是复数
	plane[0] += Scalar::all(1);//傅立叶变换后的图片不好分析，进行对数处理，结果比较好看
	log(plane[0], plane[0]);// float型的灰度空间为[0，1])
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX);//归一化便于显示

	idft(BLUR, BLUR);//idft二维傅里叶变化的结果也为复数
	split(BLUR, plane);//分离通道，主要获取通道
	magnitude(plane[0], plane[1], plane[0]); //求幅值(模)
	normalize(plane[0], plane[0], 1, 0, CV_MINMAX); //归一化便于显示
	return plane[0];//返回参数

}
//拉普拉斯滤波器传递函数
Mat laplace_kernel(Mat &src)
{
	Mat laplace_pass(src.size(), CV_32FC2);
	int row_num = src.rows;
	int col_num = src.cols;
	for (int i = 0; i < row_num; i++)
	{
		float *p = laplace_pass.ptr<float>(i);
		for (int j = 0; j < col_num; j++)
		{
			float d = pow((i - row_num / 2), 2) + pow((j - col_num / 2), 2);
			p[2 * j] = -4 * CV_PI * CV_PI * d;//应用公式
			p[2 * j + 1] = -4 * CV_PI * CV_PI * d;
		}
	}
	cv::Mat temp[] = { cv::Mat::zeros(src.size(), CV_32FC1),
					 cv::Mat::zeros(src.size(), CV_32FC1) };
	cv::split(laplace_pass, temp);
	std::string name = "laplace滤波器";
	cv::Mat show;
	cv::normalize(temp[0], show, 1, 0, CV_MINMAX);
	cv::imshow(name, show);
	return laplace_pass;
}
//laplace滤波器封装
cv::Mat laplace_filter(cv::Mat &src)
{
	cv::Mat padded = image_make_border(src);
	cv::Mat lap_kernel = laplace_kernel(padded);
	cv::Mat result =frequence_filter(padded, lap_kernel);
	return result;
}


int main()
{
	Mat img = imread("C:/Users/征途/Desktop/vs-cpp/第四章/01.jpg", IMREAD_GRAYSCALE);
	cv::Mat ideal4 = laplace_filter(img);
	ideal4 = ideal4(cv::Rect(0, 0, img.cols, img.rows));
	imshow("img4", ideal4);
	waitKey(0);
	return 0;

}

4.4.5 同态滤波器

同态滤波是把频率过滤和灰度变换结合起来的一种图像处理方法，它依靠图像的照度/ 反射率模型作为频域处理的基础，利用压缩亮度范围和增强对比度来改善图像的质量。使用这种方法可以使图像处理符合人眼对于亮度响应的非线性特性，避免了直接对图像进行傅立叶变换处理的失真。
1、对图片的照射分量和反射分量的处理
一幅图像f(x,y)可以表示为其照射分量i(x,y)和反射分量r(x,y)的乘积，即：
f(x,y) = i(x,y)r(x,y)
其中f(x, y)代表原图像，i(x,y)代表照射强度，r(x,y)代表反射强度，
一般的图像光照是均匀变化的，所以i应该是低频分量，而不同的物体对光的反射是具有突变型的，所以r(x,y)是高频分量
同态滤波实现步骤：

    上式不能直接用于对照射和反射的频率分量进行操作，因为乘积的傅里叶变换不是变换的乘积。

因此采用对数处理，并且针对对数式进行傅里叶变换：

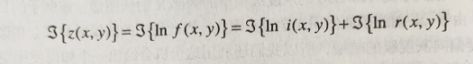
或者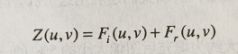

使用一个同态滤波器H(u,v)对图像的Z(u,v)进行滤波：

在空间域中滤波后的图像为:

最后取结果的指数来消除前面所取的指数：

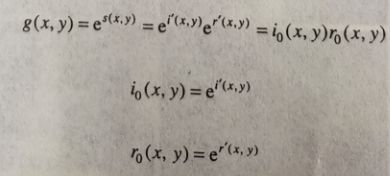
上图上面的i0(x,y)和r0(x,y)是输出（处理后）图像的照射和反射分量。
上述的方法是以称为同台系统的一类系统的特殊情况。重点是将一幅图像的照射分量和反射分量进行分离，然后再通过同态滤波H(u,v)对分量进行操作。

2、高斯同态滤波器传递函数
图像的照射分量通常由慢的空间变化来表征，而反射分量引起突变，特别是在不同物体的连接部分。
因此导致图像取对数后的傅里叶变换的低频成分与照射相联系，而高频成分与反射相联系。同态滤波器通过滤波器函数H（u,v）可以用不同的可控方法影响傅里叶变换的低频和高频分量。

高斯同态滤波器传递函数：
其中D(U,V)是距离中心的距离，由前面的式子确定，常数c控制函数坡度的锐利度，它在γL和γH之间过度。
如果γL和γH选定， 而γL<1 和γH>1,那么下图滤波器函数趋向衰减低频（照射）的贡献，而增强高频（反射）的贡献。最终结果是同时进行动态范围的压缩和对比度的增强。
同态滤波器的传递函数一般在低频部分小于1，高频部分大于1。

3、实现代码如下：

#include
#include
#include
#include
#include 
using namespace std;
using namespace cv;

//确定函数
Mat HomoFilter(cv::Mat src)
{
	src.convertTo(src, CV_64FC1);//转换数据类型
	int rows = src.rows;
	int cols = src.cols;
	int m = rows % 2 == 1 ? rows + 1 : rows;//三目运算符
	int n = cols % 2 == 1 ? cols + 1 : cols;
	copyMakeBorder(src, src, 0, m - rows, 0, n - cols, BORDER_CONSTANT, Scalar::all(0));//CopyMakeBorder复制图像并且制作边界。
	rows = src.rows;
	cols = src.cols;
	Mat dst(rows, cols, CV_64FC1);//输出

	//1、求对数
	for (int i = 0; i < rows; i++) {
		double *srcdata = src.ptr<double>(i);
		double *logdata = src.ptr<double>(i);
		for (int j = 0; j < cols; j++) {
			logdata[j] = log(srcdata[j] + 0.0001);
		}
	}
	//2.dct离散余弦变换
	Mat mat_dct = Mat::zeros(rows, cols, CV_64FC1);
	dct(src, mat_dct);

	//3. 高斯同态滤波器
	Mat H_u_v;
	double gammaH = 1.5;//1   高频增益
	double gammaL = 0.5;//<1   低频增益
	double C = 1;//斜面锐化常数 斜率
	double  d0 = (src.rows / 2) * (src.rows / 2) + (src.cols / 2) * (src.cols / 2);//double  d0 = 150;//5-200  截止频率 越大越亮
	double  d2 = 0;
	H_u_v = Mat::zeros(rows, cols, CV_64FC1);
	for (int i = 0; i < rows; i++)
	{
		double * dataH_u_v = H_u_v.ptr<double>(i);
		for (int j = 0; j < cols; j++) {
			d2 = pow(i, 2.0) + pow(j, 2.0);
			dataH_u_v[j] = (gammaH - gammaL) * (1 - exp(-C * d2 / d0)) + gammaL;
		}
	}
	H_u_v.ptr<double>(0)[0] = 1.1;
	mat_dct = mat_dct.mul(H_u_v);

	//4.idct
	idct(mat_dct, dst);//离散余弦反转换的公式
	//exp
	for (int i = 0; i < rows; i++) 
	{
		double  *srcdata = dst.ptr<double>(i);
		double *dstdata = dst.ptr<double>(i);
		for (int j = 0; j < cols; j++)
		{
			dstdata[j] = exp(srcdata[j]);
		}
	}
	dst.convertTo(dst, CV_8UC1);
	return dst;

}

//主函数
int main()
{
	Mat src = cv::imread("C:/Users/征途/Desktop/vs-cpp/第四章/同态.jpg");
	imshow("origin", src);
	int originrows = src.rows;
	int origincols = src.cols;
	Mat dst(src.rows, src.cols, CV_8UC3);
	cvtColor(src, src, COLOR_BGR2YUV);//转化为YUV通道

	vector <Mat> yuv;//创建vector对象yuv
	split(src, yuv);//将src通道分离
	Mat nowY = yuv[0];
	Mat newY = HomoFilter(nowY);
	Mat tempY(originrows, origincols, CV_8UC1);
	for (int i = 0; i < originrows; i++) 
	{
		for (int j = 0; j < origincols; j++) 
		{
			tempY.at<uchar>(i, j) = newY.at<uchar>(i, j);
		}
	}
	yuv[0] = tempY;
	merge(yuv, dst);//通道合并，merge()是C++标准库的函数，主要实现函数的排序和合并
	cvtColor(dst, dst, COLOR_YUV2BGR);
	imshow("result", dst);
	waitKey(0);
}