DBSCAN与层次聚类分析

关Kmeans聚类算法的理论和实战，也提到了该算法的两个致命缺点，一是聚类效果容易受到异常样本点的影响；二是该算法无法准确地将非球形样本进行合理的聚类。
即基于密度的聚类DBSCAN（Density-Based Special Clustering of Applications with Noise），“密度”可以理解为样本点的紧密程度，而紧密度的衡量则需要使用半径和最小样本量进行评估，如果在指定的半径领域内，实际样本量超过给定的最小样本量阈值，则认为是密度高的对象。DBSCAN密度聚类算法可以非常方便地发现样本集中的异常点，故通常可以使用该算法实现异常点的检测。

同时，也会介绍层次聚类算法，该算法比较适合小样本的聚类，它是通过计算各个簇内样本点之间的相似度，进而构建一棵有层次的嵌套聚类树。该算法仍然不适合非球形样本的聚类，但它与Kmeans算法类似，可以通过人为设定聚类个数实现样本点的聚合，相比于密度聚类来说，似乎会方便很多。

密度聚类算法

cluster.DBSCAN(eps=0.5, min_samples=5, metric='euclidean', metric_params=None,
	algorithm='auto', leaf_size=30, p=None, n_jobs=1)
	
eps：用于设置密度聚类中的ε领域，即半径，默认为0.5。

min_samples：用于设置ε领域内最少的样本量，默认为5。

metric：用于指定计算点之间距离的方法，默认为欧氏距离。

metric_params：用于指定metric所对应的其他参数值。

algorithm：在计算点之间距离的过程中，用于指定搜寻最近邻样本点的算法。默认
为'auto'，表示密度聚类会自动选择一个合适的搜寻方法。如果为'ball_tree'，则表示使用球树搜寻最近邻。如果为'kd_tree'，则表示使用K-D树搜寻最近邻。如果为'brute'，则表示使用暴力法搜寻最近邻。有关这几种最近邻搜寻方法，可以参考第11章的内容。

leaf_size：当参数algorithm为'ball_tree'或'kd_tree'时，用于指定树的叶子节点中所包含的最多样本量，默认为30；该参数会影响搜寻树的构建和搜寻最近邻的速度。

p：当参数metric为闵可夫斯基（'minkowski'）距离时，p=1，表示计算点之间的曼哈顿距离；p=2，表示计算点之间的欧氏距离；该参数的默认值为2。

n_jobs：用于设置密度聚类算法并行计算所需的CPU数量，默认为1，表示仅使用1个CPU运行算法，即不使用并行运算功能。

需要说明的是，在DBSCAN类中，参数eps和min_samples需要同时调参，即通常会指定几个候选值，并从候选值中挑选出合理的阈值。在参数eps固定的情况下，参数min_samples越大，所形成的核心对象就越少，往往会误判出许多异常点，聚成的簇数目也会增加。反之，会产生大量的核心对象，导致聚成的簇数目减少。在参数min_samples固定的情况下，参数eps越大，就
会导致越多的点落入到ε领域内，进而使核心对象增多，最终使聚成的簇数目减少；反之，会导致核心对象大量减少、最终聚成的簇数目增多。在参数eps和min_samples不合理的情况下，簇数目的增加或减少往往都是错误的。例如，应该聚为一类的样本由于簇数目的增加而聚为多类，不该聚为一类的样本由于簇数目的减少而聚为一类。

密度聚类与Kmeans的比较

means聚类的短板是无法对非球形的簇进行聚类，同时也非常容易受到极端值的影响，而密度聚类则可以弥补它的缺点。如果用于聚类的原始数据集为类球形，那么密度聚类和Kmeans聚类的效果基本一致。接下来通过图形的方式对比两种算法的聚类效果。首先通过随机抽样的方式形成两个球形簇的样本集，然后对比密度聚类和Kmeans聚类算法的聚类结构，

# 导入第三方模块
import pandas as pd
import numpy as np
#from sklearn.datasets.samples_generator import make_blobs
from sklearn.datasets import make_blobs

import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import cluster

# 模拟数据集
X,y = make_blobs(n_samples = 2000, centers = [[-1,-2],[1,3]], cluster_std = [0.5,0.5], random_state = 1234)
# 将模拟得到的数组转换为数据框，用于绘图
plot_data = pd.DataFrame(np.column_stack((X,y)), columns = ['x1','x2','y'])
# 设置绘图风格
plt.style.use('ggplot')
# 绘制散点图（用不同的形状代表不同的簇）
sns.lmplot('x1', 'x2', data = plot_data, hue = 'y',markers = ['^','o'],
           fit_reg = False, legend = False)
# 显示图形
plt.show()

# 导入第三方模块
from sklearn import cluster
# 构建Kmeans聚类和密度聚类
kmeans = cluster.KMeans(n_clusters=2, random_state=1234)
kmeans.fit(X)
dbscan = cluster.DBSCAN(eps = 0.5, min_samples = 10)
dbscan.fit(X)
# 将Kmeans聚类和密度聚类的簇标签添加到数据框中
plot_data['kmeans_label'] = kmeans.labels_
plot_data['dbscan_label'] = dbscan.labels_

# 绘制聚类效果图
# 设置大图框的长和高
plt.figure(figsize = (12,6))
# 设置第一个子图的布局
ax1 = plt.subplot2grid(shape = (1,2), loc = (0,0))
# 绘制散点图
ax1.scatter(plot_data.x1, plot_data.x2, c = plot_data.kmeans_label)
# 设置第二个子图的布局
ax2 = plt.subplot2grid(shape = (1,2), loc = (0,1))
# 绘制散点图(为了使Kmeans聚类和密度聚类的效果图颜色一致，通过序列的map“方法”对颜色作重映射)
ax2.scatter(plot_data.x1, plot_data.x2, c=plot_data.dbscan_label.map({-1:1,0:2,1:0}))
# 显示图形
plt.show()

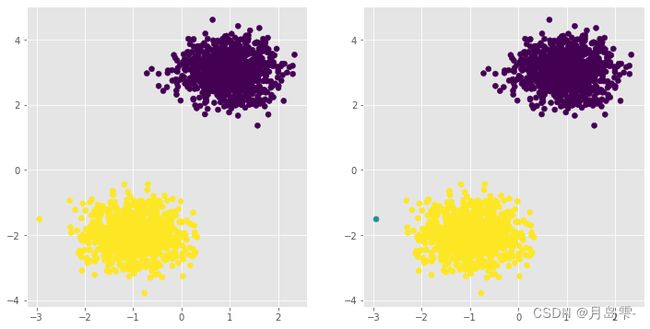
对于两个球形簇的样本点而言，不管是Kmeans聚类（左图）还是密度聚类
（右图）都能够很好地将样本聚为两个簇。所不同的是，密度聚类发现了一个异常点（如图中虚线圈内的点），它不属于任何一个簇。所以，密度聚类算法既可以在球形簇得到很好的效果，又可以发现远离簇的异常点。
对于非球形簇的样本点而言，再来看看两个算法在聚类过程中的差异，样本数据仍然采用随机抽样的方式

# 导入第三方模块
from sklearn.datasets import make_moons
# 构造非球形样本点
X1,y1 = make_moons(n_samples=2000, noise = 0.05, random_state = 1234)
# 构造球形样本点
X2,y2 = make_blobs(n_samples=1000, centers = [[3,3]], cluster_std = 0.5, random_state = 1234)
# 将y2的值替换为2(为了避免与y1的值冲突，因为原始y1和y2中都有0这个值)
y2 = np.where(y2 == 0,2,0)
# 将模拟得到的数组转换为数据框，用于绘图
plot_data = pd.DataFrame(np.row_stack([np.column_stack((X1,y1)),np.column_stack((X2,y2))]), columns = ['x1','x2','y'])

# 绘制散点图（用不同的形状代表不同的簇）
sns.lmplot('x1', 'x2', data = plot_data, hue = 'y',markers = ['^','o','>'],
           fit_reg = False, legend = False)
# 显示图形
plt.show()

# 构建Kmeans聚类和密度聚类
kmeans = cluster.KMeans(n_clusters=3, random_state=1234)
kmeans.fit(plot_data[['x1','x2']])
dbscan = cluster.DBSCAN(eps = 0.3, min_samples = 5)
dbscan.fit(plot_data[['x1','x2']])
# 将Kmeans聚类和密度聚类的簇标签添加到数据框中
plot_data['kmeans_label'] = kmeans.labels_
plot_data['dbscan_label'] = dbscan.labels_

# 绘制聚类效果图
# 设置大图框的长和高
plt.figure(figsize = (12,6))
# 设置第一个子图的布局
ax1 = plt.subplot2grid(shape = (1,2), loc = (0,0))
# 绘制散点图
ax1.scatter(plot_data.x1, plot_data.x2, c = plot_data.kmeans_label)
# 设置第二个子图的布局
ax2 = plt.subplot2grid(shape = (1,2), loc = (0,1))
# 绘制散点图(为了使Kmeans聚类和密度聚类的效果图颜色一致，通过序列的map“方法”对颜色作重映射)
ax2.scatter(plot_data.x1, plot_data.x2, c=plot_data.dbscan_label.map({-1:1,0:0,1:3,2:2}))
# 显示图形
plt.show()

对于原始三个簇的样本点而言，当其中的样本簇不满足球形时，Kmeans聚
类效果就非常不理想，会将原本不属于一类的样本点聚为一类（如左图所示），而对应的密度聚类就可以非常轻松地将非球形簇准确地划分开来（如右图所示）。在上面的图形中，再次验证了Kmeans聚类和密度聚类在对待球形簇的时候，聚类效果都比较出色。右图中的四个点仍然是通过密度聚类算法得到的异常点，但对于Kmeans聚类来说，并不会直接给出异常数据。

层次聚类

层次聚类的实质是计算各簇内样本点之间的相似度，并通过相似度的结果构建凝聚或分裂的层次树。凝聚树是一种自底向上的造树过程，起初将每一个样本当作一个类，然后通过计算样本间或簇间的距离进行样本合并，最终形成一个包含所有样本的大簇；分裂树与凝聚树恰好相反，它是自顶向下的造树过程，起初将所有样本点聚为一个类，然后利用相似度的方法将大簇进行分割，直到所有样本为一个类为止。

运用Python可以非常方便地将层次聚类算法落地到实际工作中，只需导入sklearn中的cluster子模块，并从中调用AgglomerativeClustering类即可

cluster.AgglomerativeClustering(n_clusters=2, affinity='euclidean', memory=None,
	connectivity=None, compute_full_tree='auto', linkage='ward')
	
n_clusters：用于指定样本点聚类的个数，默认为2。

affinity：用于指定样本间距离的衡量指标，可以是欧氏距离、曼哈顿距离、余弦相似度等，默认为'euclidean'；如果参数linkage为'ward'，该参数只能设置为欧氏距离。

memory：是否指定缓存结果的输出，默认为否；如果该参数设置为一个路径，最终将把计算过程的缓存输出到指定的路径中。

connectivity：用于指定一个连接矩阵。

compute_full_tree：通常情况下，当聚类过程达到n_clusters时，算法就会停止，如果该参数设置为True，则表示算法将生成一棵完整的凝聚树。

linkage：用于指定簇间距离的衡量指标，默认为'ward'，表示最小距离法；如果
为'complete'，则表示使用最大距离法；如果为'average'，则表示使用平均距离法。

层次聚类法对于球形簇的样本点会有更佳的聚类效果，接下来将随机生成
两个球形簇的样本点，并利用层次聚类算法对它们进行聚类，比较三种簇间的距离指标所形成聚类差异

# 构造两个球形簇的数据样本点
X,y = make_blobs(n_samples = 2000, centers = [[-1,0],[1,0.5]], cluster_std = [0.2,0.45], random_state = 1234)
# 将模拟得到的数组转换为数据框，用于绘图
plot_data = pd.DataFrame(np.column_stack((X,y)), columns = ['x1','x2','y'])
# 绘制散点图（用不同的形状代表不同的簇）
sns.lmplot('x1', 'x2', data = plot_data, hue = 'y',markers = ['^','o'],
           fit_reg = False, legend = False)
# 显示图形
plt.show()

# 设置大图框的长和高
plt.figure(figsize = (16,5))
# 设置第一个子图的布局
ax1 = plt.subplot2grid(shape = (1,3), loc = (0,0))
# 层次聚类--最小距离法
agnes_min = cluster.AgglomerativeClustering(n_clusters = 2, linkage='ward')
agnes_min.fit(X)
# 绘制聚类效果图
ax1.scatter(X[:,0], X[:,1], c=agnes_min.labels_)

# 设置第二个子图的布局
ax2 = plt.subplot2grid(shape = (1,3), loc = (0,1))
# 层次聚类--最大距离法
agnes_max = cluster.AgglomerativeClustering(n_clusters = 2, linkage='complete')
agnes_max.fit(X)
ax2.scatter(X[:,0], X[:,1], c=agnes_max.labels_)

# 设置第三个子图的布局
ax2 = plt.subplot2grid(shape = (1,3), loc = (0,2))
# 层次聚类--平均距离法
agnes_avg = cluster.AgglomerativeClustering(n_clusters = 2, linkage='average')
agnes_avg.fit(X)
plt.scatter(X[:,0], X[:,1], c=agnes_avg.labels_)
plt.show()

左图为最小距离法形成的聚类效果；中图为最大距离法构成的聚类效果；
右图为平均距离法完成的聚类效果。很显然，最小距离法与平均距离法的聚类效果完全一样，并且相比于原始样本点，只有三个样本点被错误聚类，即图中虚线框内所包含的三个点。但是利用最大距离法所产生的聚类效果要明显差很多，主要是由于模糊地带（原始数据中两个簇交界的区域）的异常点夸大了簇之间的距离。

密度聚类与层次聚类的应用

里以我国31个省份的人口出生率和死亡率两个维度的数据为例，对其进行聚类分析。首先，将数据读入Python中，并绘制出生率和死亡率数据的散点图，代码如下：

# 读取外部数据
Province = pd.read_excel(r'Province.xlsx')
Province.head()
# 绘制出生率与死亡率散点图
plt.scatter(Province.Birth_Rate, Province.Death_Rate, c = 'steelblue')
# 添加轴标签
plt.xlabel('Birth_Rate')
plt.ylabel('Death_Rate')
# 显示图形
plt.show()

# 读入第三方包
from sklearn import preprocessing
# 选取建模的变量
predictors = ['Birth_Rate','Death_Rate']
# 变量的标准化处理
X = preprocessing.scale(Province[predictors])
X = pd.DataFrame(X)

# 构建空列表，用于保存不同参数组合下的结果
res = []
# 迭代不同的eps值
for eps in np.arange(0.001,1,0.05):
    # 迭代不同的min_samples值
    for min_samples in range(2,10):
        dbscan = cluster.DBSCAN(eps = eps, min_samples = min_samples)
        # 模型拟合
        dbscan.fit(X)
        # 统计各参数组合下的聚类个数（-1表示异常点）
        n_clusters = len([i for i in set(dbscan.labels_) if i != -1])
        # 异常点的个数
        outliners = np.sum(np.where(dbscan.labels_ == -1, 1,0))
        # 统计每个簇的样本个数
        stats = str(pd.Series([i for i in dbscan.labels_ if i != -1]).value_counts().values)
        res.append({'eps':eps,'min_samples':min_samples,'n_clusters':n_clusters,'outliners':outliners,'stats':stats})
# 将迭代后的结果存储到数据框中        
df = pd.DataFrame(res)

# 根据条件筛选合理的参数组合
df.loc[df.n_clusters == 3, :]

	eps	min_samples	n_clusters	outliners	stats
40	0.251	2	3	23	[3 3 2]
57	0.351	3	3	19	[6 3 3]
88	0.551	2	3	7	[17 5 2]
96	0.601	2	3	7	[17 5 2]
104	0.651	2	3	5	[17 7 2]
112	0.701	2	3	5	[17 7 2]
129	0.801	3	3	4	[17 7 3]
136	0.851	2	3	2	[24 3 2]
144	0.901	2	3	1	[24 4 2]
152	0.951	2	3	1	[24 4 2]

一方面，不管是Kmeans聚类、密度聚类还是层次聚类，读者都需要养成一个好习惯，即对用于聚类的原始数据做标准化处理，这样可以避免不同量纲的影响；另一方面，对于密度聚类而言，通常都需要不停地调试参数eps和min_samples，因为该算法的聚类效果在不同的参数组合下会有很大的差异。如表16-4所示，如果需要将数据聚为3类，则得到如上几种参数组合，这里不妨选择eps为0.801、min_samples为3的参数值（因为该参数组合下的异常点个数比较合理）。这里还有一个问题需要解决，那就是将样本点聚为几类比较合理。一般建议选择两种解决方案：一种是借助于第15章所介绍的轮廓系数法，即初步使用Kmeans算法对聚类个数做探索性分析；另一种是采用统计学中的主成分分析法，对原始的多变量数据进行降维，绝大多数情况下，两个主成分基本可以覆盖原始数据80%左右的信息，从而可以根据主成分绘制对应的散点图，并通过肉眼发现数据点的分布块。接下来，利用如上所得的参数组合，构造密度聚类模型，实现原始数据集的聚类

# 中文乱码和坐标轴负号的处理
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False

# 利用上述的参数组合值，重建密度聚类算法
dbscan = cluster.DBSCAN(eps = 0.801, min_samples = 3)
# 模型拟合
dbscan.fit(X)
Province['dbscan_label'] = dbscan.labels_
# 绘制聚类聚类的效果散点图
sns.lmplot(x = 'Birth_Rate', y = 'Death_Rate', hue = 'dbscan_label', data = Province,
           markers = ['*','d','^','o'], fit_reg = False, legend = False)
# 添加省份标签
for x,y,text in zip(Province.Birth_Rate,Province.Death_Rate, Province.Province):
    plt.text(x+0.1,y-0.1,text, size = 8)
# 添加参考线
plt.hlines(y = 5.8, xmin = Province.Birth_Rate.min(), xmax = Province.Birth_Rate.max(), 
           linestyles = '--', colors = 'red')
plt.vlines(x = 10, ymin = Province.Death_Rate.min(), ymax = Province.Death_Rate.max(), 
           linestyles = '--', colors = 'red')
# 添加轴标签
plt.xlabel('Birth_Rate')
plt.ylabel('Death_Rate')
# 显示图形
plt.show()

三角形、菱形和圆形所代表的点即为三个不同的簇，五角星所代表的点
即为异常点，这个聚类效果还是非常不错的，对比建模之前的结论非常吻合。从图16-17可知，以北京、天津、上海为代表的省份，属于低出生率和低死亡率类型；广东、宁夏和新疆三个省份属于高出生率和低死亡率类型；江苏、四川、湖北为代表的省份属于高出生率和高死亡率类型。四个异常中，黑龙江与辽宁比较相似，属于低出生率和高死亡率类型；山东省属于极高出生率和高死亡率的省份；西藏属于高出生率和低死亡率的省份，但它与广东、宁夏和新疆更为相似。同理，再使用层次聚类算法，对该数据集进行聚类，并比较其与密度聚类之间的差异

# 利用最小距离法构建层次聚类
agnes_min = cluster.AgglomerativeClustering(n_clusters = 3, linkage='ward')
# 模型拟合
agnes_min.fit(X)
Province['agnes_label'] = agnes_min.labels_
# 绘制层次聚类的效果散点图
sns.lmplot(x = 'Birth_Rate', y = 'Death_Rate', hue = 'agnes_label', data = Province,
           markers = ['d','^','o'], fit_reg = False, legend = False)
# 添加轴标签
plt.xlabel('Birth_Rate')
plt.ylabel('Death_Rate')
# 显示图形
plt.show()

由于层次聚类不会返回异常点的结果，故图中的所有散点聚成了三个簇。与密度聚类相比，除了将异常点划分到对应的簇中，其他点均被正确地聚类。
为了对比第15章的内容，这里利用Kmeans算法对该数据集进行聚类，聚类之前利用轮廓系数法判断合理的聚类个数

# 导入第三方模块
from sklearn import metrics
# 构造自定义函数，用于绘制不同k值和对应轮廓系数的折线图
def k_silhouette(X, clusters):
    K = range(2,clusters+1)
    # 构建空列表，用于存储个中簇数下的轮廓系数
    S = []
    for k in K:
        kmeans = cluster.KMeans(n_clusters=k)
        kmeans.fit(X)
        labels = kmeans.labels_
        # 调用字模块metrics中的silhouette_score函数，计算轮廓系数
        S.append(metrics.silhouette_score(X, labels, metric='euclidean'))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')    
    # 绘制K的个数与轮廓系数的关系
    plt.plot(K, S, 'b*-')
    plt.xlabel('簇的个数')
    plt.ylabel('轮廓系数')
    # 显示图形
    plt.show()
    
# 聚类个数的探索
k_silhouette(X, clusters = 10)

当簇的个数为3时，轮廓系数达到最大，说明将各省份出生率与死亡率数
据集聚为3类比较合理，这也恰好验证了之前肉眼所观察得到的结论

# 利用Kmeans聚类
kmeans = cluster.KMeans(n_clusters = 3)
# 模型拟合
kmeans.fit(X)
Province['kmeans_label'] = kmeans.labels_
# 绘制Kmeans聚类的效果散点图
sns.lmplot(x = 'Birth_Rate', y = 'Death_Rate', hue = 'kmeans_label', data = Province,
           markers = ['d','^','o'], fit_reg = False, legend = False)
# 添加轴标签
plt.xlabel('Birth_Rate')
plt.ylabel('Death_Rate')
plt.show()

Kmeans聚类与层次聚类的效果完全一致。从上面的分析结果可知，该数据集仍然为球形分布的数据，因为密度聚类、层次聚类和Kmeans聚类的效果几乎一致，所不同的是密度聚类可以非常方便地发现数据中的异常点