机器学习保姆级入门案例-波士顿房价预测
利用scikit-learn进行机器学习入门案例
相信很多人都是知道波士顿房价的数据集,一个非常经典的机器学习入门案例数据集。在这个案例中直接使用sklearn中自带的数据集来进行数据分析和建模,主要内容包含:
- 数据探索
- 相关性分析
- 变量研究
- 线性回归模型探索
- 模型改进
导入库
import numpy as np
import pandas as pd
import hvplot.pandas
import matplotlib.pyplot as plt
%matplotlib inline
# 使输出的图像以更高清的方式显示
%config InlineBackend.figure_format = 'retina'
import seaborn as sns
# plt.style.use('ggplot')
plt.style.use("fivethirtyeight")
# Pandas中只显示3位小数
pd.set_option('display.float_format', lambda x: '{:.3f}'.format(x))
from sklearn import datasets # 导入数据集
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import warnings
导入内置数据
导数据
从sklearn中导入内置的波士顿房价数据集:
boston = datasets.load_boston()
X = boston.data # 特征值
y = boston.target # 目标变量
df = pd.DataFrame(
X,
columns = boston.feature_names
)
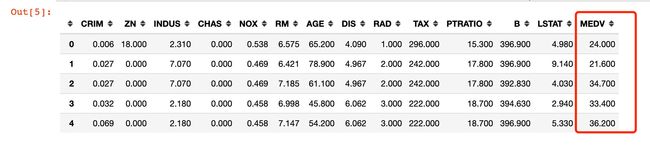
df.head()
df["MEDV"] = y
df.head()
查看数据字段、类型:
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 506 entries, 0 to 505
Data columns (total 14 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 CRIM 506 non-null float64
1 ZN 506 non-null float64
2 INDUS 506 non-null float64
3 CHAS 506 non-null float64
4 NOX 506 non-null float64
5 RM 506 non-null float64
6 AGE 506 non-null float64
7 DIS 506 non-null float64
8 RAD 506 non-null float64
9 TAX 506 non-null float64
10 PTRATIO 506 non-null float64
11 B 506 non-null float64
12 LSTAT 506 non-null float64
13 MEDV 506 non-null float64
dtypes: float64(14)
memory usage: 55.5 KB
字段说明
字段对应的中文解释,来自网上的说明:
- CRIM:城镇人均犯罪率
- ZN: 占地面积超过2.5万平方英尺的住宅用地比例
- INDUS:城镇上非零售业务地区的 比例
- CHAS:虚拟变量;如果土地在查尔斯河,取值1;否则为0
- NOX:一氧化氮浓度
- RM:平均每个居民房数
- AGE:在1940年之前建成的所有者占用单位的比例
- DIS: 与波士顿的5个就业中心之间的加权距离
- RAD: 辐距离住房最近的公路入口编号
- TAX:每10,000美元的全额物业税
- PTRATIO:城镇师生比例大小
- B:1000(Bk-0.63)^2,其中 Bk 指代城镇中黑人的比例
- LSTAT:全部人口中地位较低人群的百分数大小
- MEDV:目标变量,以1000美元来进行计算的自由住房的中位数大小
基本信息
数据形状和缺失值情况:
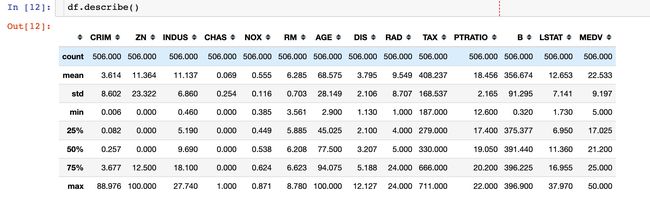
统计信息
数据统计信息主要是针对数值型的字段。这个案例中的数据刚刚好都是数值型字段,能够迅速看到每个字段的:中值、方差、最小值、四分之一分位数等
相关性检验
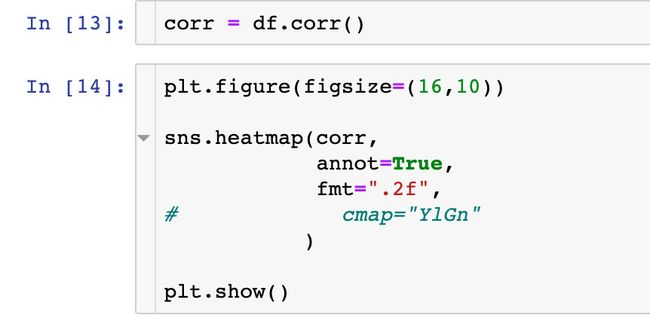
计算相关系数
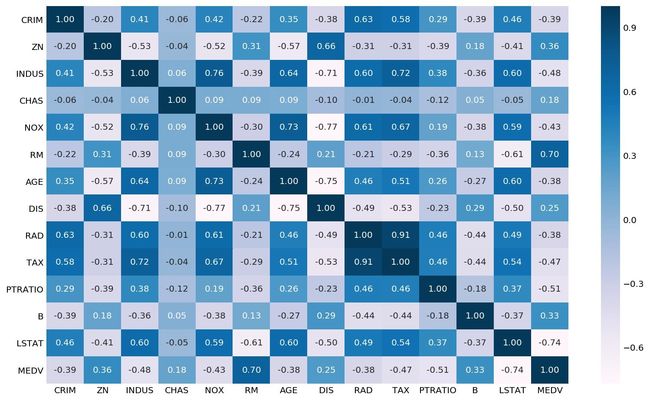
绘制相关系数的热力分布图:
查看每个特征和目标变量MEDV之间的相关系数:
corr["MEDV"].sort_values()
LSTAT -0.738
PTRATIO -0.508
INDUS -0.484
TAX -0.469
NOX -0.427
CRIM -0.388
RAD -0.382
AGE -0.377
CHAS 0.175
DIS 0.250
B 0.333
ZN 0.360
RM 0.695
MEDV 1.000
Name: MEDV, dtype: float64
从绝对值的角度来看:LSTAT、RM、PTRATIO这3个字段是最具有相关性的~
多变量研究
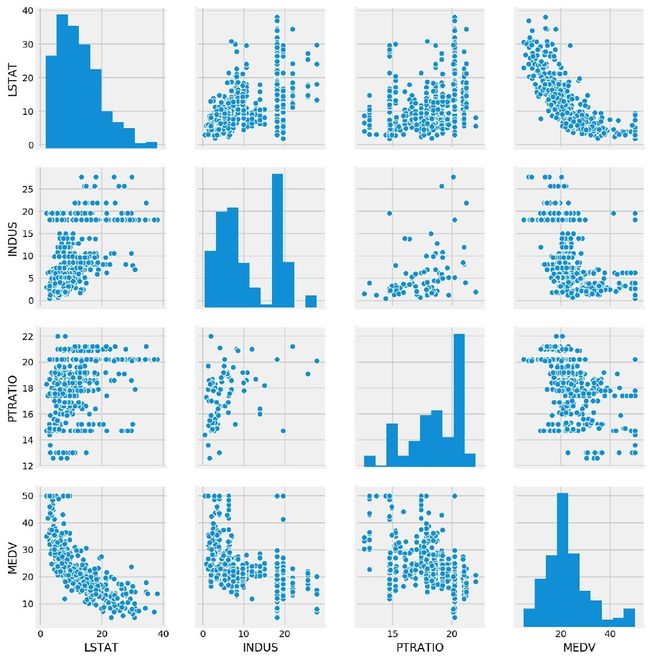
研究不同自变量之间、自变量和因变量之间的关系
sns.pairplot(df[["LSTAT","INDUS","PTRATIO","MEDV"]]) # 绝对值靠前3的特征
plt.show()
数据集划分
划分给定的数据集,比例是8:2
X = df.drop("MEDV",axis=1)
y = df[["MEDV"]]
X_train, X_test, y_train, y_test = train_test_split(
X, y,
test_size=0.2,
random_state=123)
线性回归模型(重点)
将506个样本13个特征组成的矩阵赋值给变量X,变量X为大写字母的原因是数学中表示矩阵使用大写字母。 将506个样本1个预测目标值组成的矩阵赋值给变量 Y。
表中13列数据就是13个是样本特征(属性),机器学习的目的就是得到一个线性回归模型,即:
Y = θ 0 + θ 1 × X 1 + θ 2 × X 2 + θ 3 × X 3 + ⋯ + θ 13 × X 13 Y=\theta_{0}+\theta_{1} \times X_{1}+\theta_{2} \times X_{2}+\theta_{3} \times X_{3}+\cdots+\theta_{13} \times X_{13} Y=θ0+θ1×X1+θ2×X2+θ3×X3+⋯+θ13×X13
线性回归模型需要学习的就是$ \theta_{0}, \theta_{1}, \theta_{2}, \cdots \theta_{13} $这14个参数,然后将y用这个13个参数来表示。
建模
from sklearn.linear_model import LinearRegression
# 模型实例化
le = LinearRegression()
# 拟合过程
le.fit(X_train, y_train)
# 得到回归系数
coef1 = le.coef_ # 13个回归系数
coef1
array([[-9.87931696e-02, 4.75027102e-02, 6.69491841e-02,
1.26954150e+00, -1.54697747e+01, 4.31968412e+00,
-9.80167937e-04, -1.36597953e+00, 2.84521838e-01,
-1.27533606e-02, -9.13487599e-01, 7.22553507e-03,
-5.43790245e-01]])
预测
# 对测试集的数据进行预测
predict1 = le.predict(X_test)
predict1[:5]
array([[16.00330023],
[27.79447431],
[39.26769478],
[18.32613556],
[30.45487494]])
指标得分
主要是考察两个指标的得分:
- 在测试集上的得分score
- 测试数据和预测数据之间的RMSE得分
# 得分
print("Score:", le.score(X_test, y_test))
print("RSME:", np.sqrt(mean_squared_error(y_test, predict1)))
Score: 0.65924665103541
RSME: 5.309659665032168
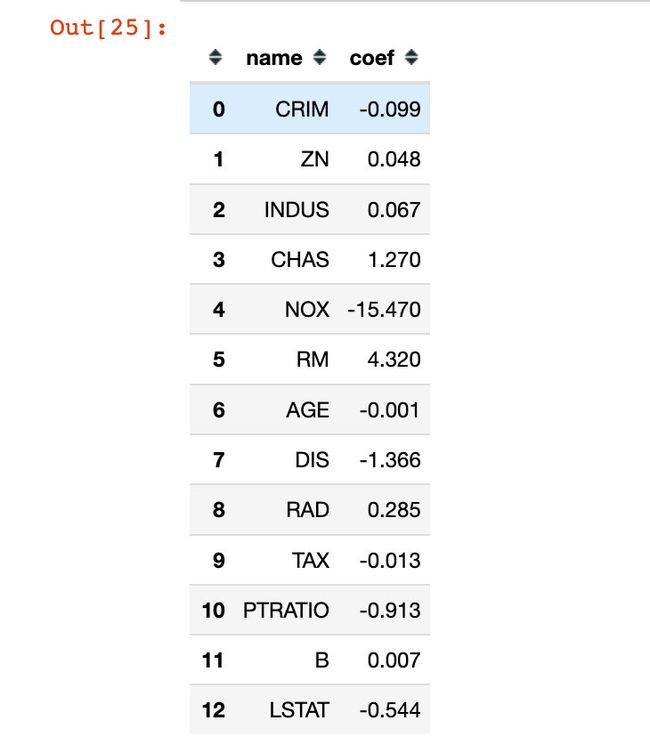
回归系数
下面是本次建模案例得到的13个回归系数:
coef1
# 结果
array([[-9.87931696e-02, 4.75027102e-02, 6.69491841e-02,
1.26954150e+00, -1.54697747e+01, 4.31968412e+00,
-9.80167937e-04, -1.36597953e+00, 2.84521838e-01,
-1.27533606e-02, -9.13487599e-01, 7.22553507e-03,
-5.43790245e-01]])
le_df = pd.DataFrame()
le_df["name"] = X.columns.tolist()
le_df["coef"] = coef1.reshape(-1,1)
le_df
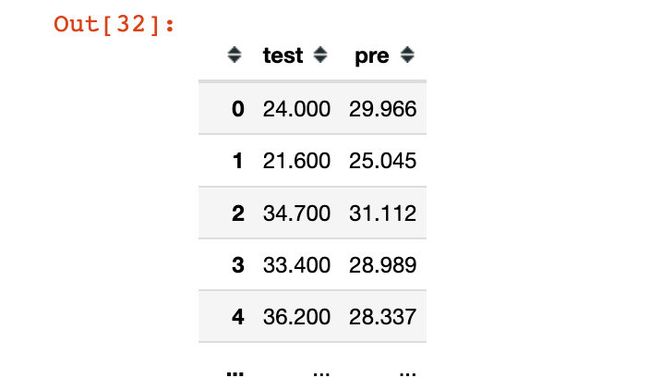
真实值和预测值的对比
test_pre = pd.DataFrame({"test": y_test["MEDV"].tolist(),
"pre": predict1.flatten()
})
test_pre
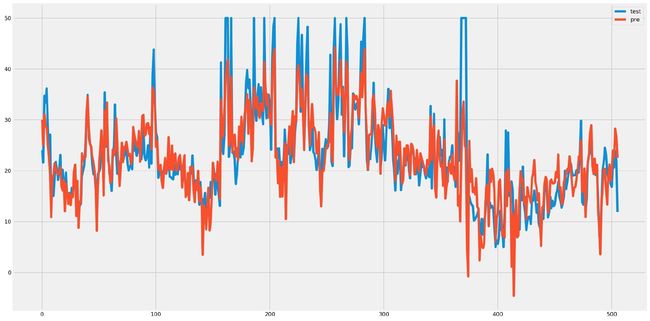
test_pre.plot(figsize=(18,10))
plt.show()
我们对比真实值和预测值的大小,发现:有42.15%左右的测试集中真实值是大于预测值
结论1
通过上面的结果我们发现:
- 超过半数的预测值是比真实值要大的,预测的房价偏高
- 波士顿房价的数据比较干净,预处理和特征工程部分的工作相对会少一些,上面的建模过程几乎没有涉及到太多特征工程的工作
模型评价
测试集上评价
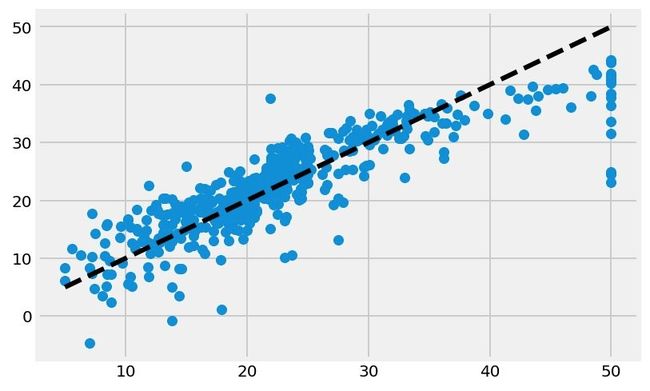
将真实值和预测值的散点分布图画在坐标轴上
plt.scatter(y_test, predict1, label="test")
plt.plot([y_test.min(), y_test.max()],
[y_test.min(), y_test.max()],
'k--',
lw=3,
label="predict"
)
plt.show()
从上图中看到:
- 在10-30之间的房价预测的更为准确些
- 当超过30后,预测的结果会偏小;上面的统计结果页表明,预测值会大于真实值
整体数据集评价
我们对整个数据集X上进行建模:
predict_all = le.predict(X)
print("Score:", le.score(X, y)) # 统一换成整体数据集
print("RSME:", np.sqrt(mean_squared_error(y, predict_all)))
Score: 0.7371217459477342
RSME: 4.710845521793303
比较整体数据集上的真实值和预测值:
all_pre = pd.DataFrame({"test": y["MEDV"].tolist(),
"pre": predict_all.flatten()
})
all_pre
all_pre.plot(figsize=(18,10))
plt.show()
plt.scatter(y, predict_all, label="y_all")
plt.plot([y.min(), y.max()],
[y.min(), y.max()],
'k--',
lw=3,
label="all_predict"
)
plt.show()
模型改进
数据标准化
from sklearn.preprocessing import StandardScaler
# 实例化
ss = StandardScaler()
# 特征数据
X = ss.fit_transform(X)
# 目标变量
y = ss.fit_transform(y)
# 先切分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=9)
决策树回归
from sklearn.tree import DecisionTreeRegressor
tr = DecisionTreeRegressor(max_depth=2)
tr.fit(X_train, y_train)
# 预测值
tr_pre = tr.predict(X_test)
# 模型评分
print('Score:{:.4f}'.format(tr.score(X_test, y_test)))
# RMSE(标准误差)
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test,tr_pre))))
Score:0.7184
RMSE:0.5810
GradientBoosting(梯度提升)
from sklearn import ensemble
gb = ensemble.GradientBoostingRegressor()
gb.fit(X_train, y_train)
gb_pre=gb.predict(X_test)
# 模型评分
print('Score:{:.4f}'.format(gb.score(X_test, y_test)))
# RMSE(标准误差)
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test,gb_pre))))
Score:0.9024
RMSE:0.3421
目前效果是最好的~
Lasso回归
Lasso的全称是:Least Absolute Shrinkage and Selection Operator
Lasso也是惩罚其回归系数的绝对值;另外一种方式岭回归,使用的是平方形式
from sklearn.linear_model import Lasso
lo = Lasso()
lo.fit(X_train, y_train)
lo_pre=lo.predict(X_test)
# 模型评分
print('Score:{:.4f}'.format(lo.score(X_test, y_test)))
# RMSE(标准误差)
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test,lo_pre))))
Score:-0.0001
RMSE:1.0949
SVR-支持向量回归
from sklearn.svm import SVR
linear_svr = SVR(kernel="linear")
linear_svr.fit(X_train, y_train)
linear_svr_pre = linear_svr.predict(X_test)
# 模型评分
print('Score:{:.4f}'.format(linear_svr.score(X_test, y_test)))
# RMSE(标准误差)
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test,linear_svr_pre))))
Score:0.7200
RMSE:0.5793
结论2
对数据进行标准化和采用不同的回归模型后,发现:
- 采用Gradient Boosting 算法的话,效果是最好的。最终的评分高达0.9017
- 在机器学习建模的过程中,数据预处理方案和特征工程的设计是很重要的,对我们最终的效果会有很大的影响
在实际工作项目中也是如此,数据预处理、特征工程、筛选有效的特征会花费数据工程师很多的精力~