Sklearn机器学习与Plotly可视化强强联合
在学习sklearn(机器学习)过程中,模型原理可谓是枯燥无味,加上大多数模型训练过程也是不可见的,这使得很多小伙伴们望而却步,当然也有很多学者试图通过各种方式以可视化模型学习及预测过程,但大多数是复杂且不美观的。
本文将给大家带来一个福音。当机器学习遇到简洁、强大且美观的plotly可视化库时,可谓是强强联手,从模型训练、预测、决策边界、残差、交叉验证、网格搜索到模型评价,均可以很容易地可视化出来。
文章目录
-
- 技术提升
- 1、Plotly基本介绍
-
- 基本图表
- 基础图表
- 统计图
- 科学图
- 金融图表
- 地图
- 3D图表
- 多子图
- 与Jupyter交互图
- 添加自定义控件
- 人工智能与机器学习图
- 2、Plotly Express 回归
-
- Plotly Express 简介
- 普通最小二乘回归可视化
-
- 单线拟合
- 多线拟合
- 查看拟合结果
- 非线性回归可视化
- 3、Sklearn与Plotly组合
-
- 线性回归可视化
-
- 模型泛化能力可视化
- KNN回归可视化
- 多项式回归可视化
- 3D图绘制支持向量机决策边界
- 多元线性回归可视化
-
- 实际点与预测点的比较图
- 增强的预测误差分析图
- 残差图
- 交叉验证可视化
- 基于决策树的网格搜索可视化
-
- 网格搜索调参
- 单个函数调用来绘制每个图形
- KNN分类可视化
- 模型评价可视化
-
- 与真实标签相比的分数直方图
- 在不同的阈值下评估模型性能
技术提升
本文由技术群粉丝分享,项目源码、数据、技术交流提升,均可加交流群获取,群友已超过2000人,添加时最好的备注方式为:来源+兴趣方向,方便找到志同道合的朋友
方式①、添加微信号:dkl88191,备注:来自CSDN +研究方向
方式②、微信搜索公众号:Python学习与数据挖掘,后台回复:加群
1、Plotly基本介绍
Plotly:协同 Python 和 matplotlib 工作的 web 绘图库
官网链接:https://plot.ly/python/
Plotly 是一款用来做数据分析和可视化的在线平台,功能非常强大,可以在线绘制很多图形比如条形图、散点图、饼图、直方图等等。而且还是支持在线编辑,以及多种语言python、javascript、matlab、R等许多API。
Plotly在Python中使用也很简单,直接用pip install plotly就可以了。推荐最好在Jupyter notebook中使用,Pycharm操作不是很方便。
Plotly的图表多样化且专业化,可以绘制很多专业学科领域的图表。下面是官网的几种划分。
基本图表
基础图表
统计图
科学图
金融图表
地图
3D图表
多子图
与Jupyter交互图
添加自定义控件
人工智能与机器学习图
本文主要深入探讨poltly与机器学习结合,绘制机器学习相关图。
2、Plotly Express 回归
这里我们将一起学习如何使用plotly图表来显示各种类型的回归模型,从简单的模型如线性回归,到其他机器学习模型如决策树和多项式回归。
重点学习plotly的各种功能,如使用不同参数对同一模型进行比较分析、Latex显示、3D表面图,以及使用plotly Express进行增强的预测误差分析。
Plotly Express 简介
Plotly Express 是plotly的易于使用的高级界面,可处理多种类型的数据并生成易于样式化的图形。
通过Plotly Express 可以将普通最小二乘回归趋势线添加到带有trendline参数的散点图中。为此需要安装statsmodels及其依赖项。
基础图形: scatter, line, area, bar, funnel, timeline
部分到整体图表: pie, sunburst, treemap, funnel_area
一维分布图: histogram, box, violin, strip
二维分布图: density_heatmap, density_contour
矩阵的输入图: imshow
三维图: scatter_3d, line_3d
多维图: scatter_matrix, parallel_coordinates, parallel_categories
平铺地图: scatter_mapbox, line_mapbox, choropleth_mapbox, density_mapbox
离线地图: scatter_geo, line_geo, choropleth
极坐标图: scatter_polar, line_polar, bar_polar
三元图: scatter_ternary, line_ternary
普通最小二乘回归可视化
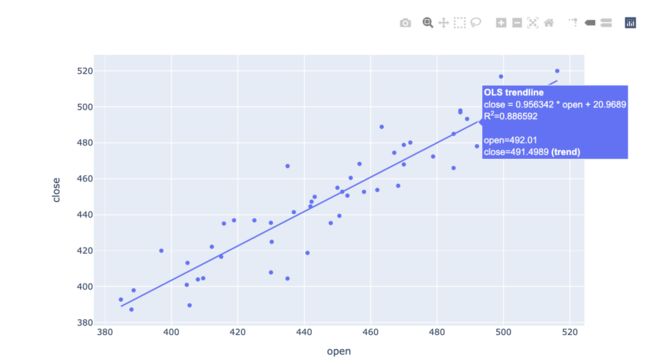
将线性普通最小二乘(OLS)回归趋势线或非线性局部加权散点图平滑(LOWESS)趋势线添加到Python中的散点图。将鼠标悬停在趋势线上将显示该线的方程式及其R平方值,非常方便。
单线拟合
与seaborn类似,plotly图表主题不需要单独设置,使用默认参数即可满足正常情况下的使用,因此一行代码并设置参数trendline="ols"即可搞定散点图与拟合线的绘制,非常方便。
import plotly.express as px
fig=px.scatter(df, x="open", y="close",
trendline="ols")
fig.show()
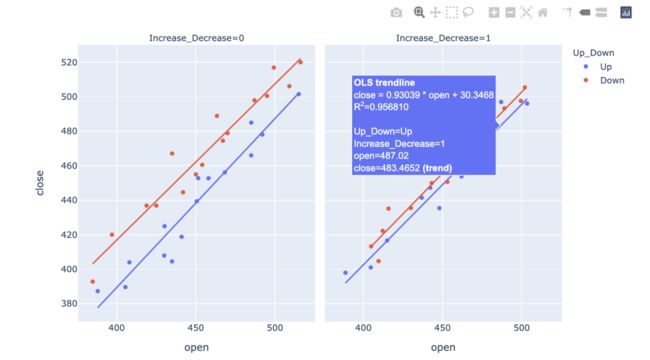
多线拟合
同样,在绘制多个变量及多个子图时,也不需要设置多画布,只要设置好参数 'x','y','facet_col','color' 即可。
fig=px.scatter(df, x="open", y="close",
facet_col="Increase_Decrease",
color="Up_Down", trendline="ols")
fig.show()
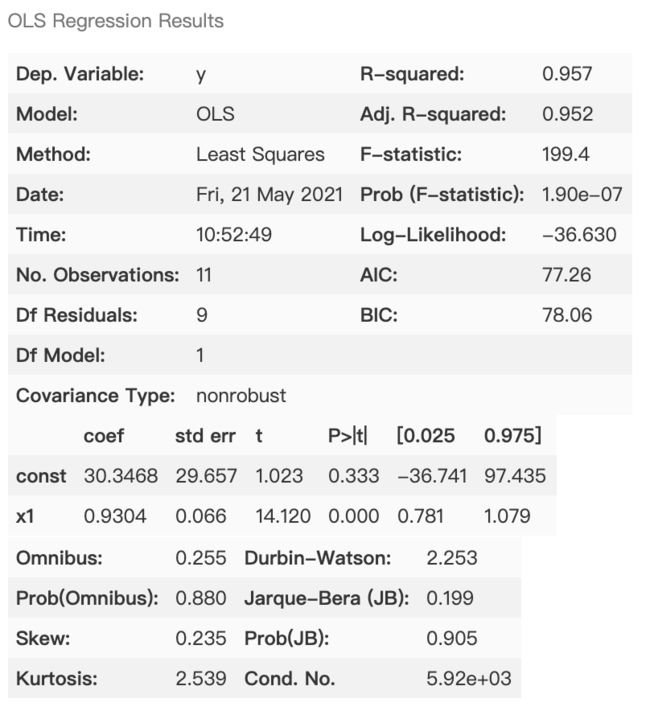
查看拟合结果
绘图后,需要查看具体的各项统计学数据,可以通过get_trendline_results方法,具体代码与结果如下。
results = px.get_trendline_results(fig)
results.query(
"Up_Down == 'Up' and Increase_Decrease == '1'"
).px_fit_results.iloc[0].summary()
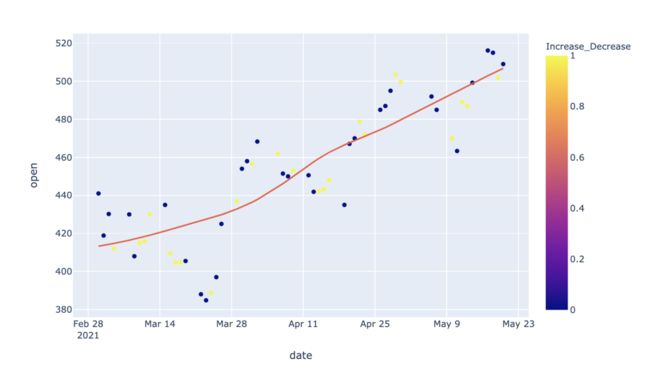
非线性回归可视化
非线性回归拟合是通过设置参数trendline="lowess"来实现,Lowess是指局部加权线性回归,它是一种非参数回归拟合的方式。
fig = px.scatter(df2, x="date", y="open",
color="Increase_Decrease",
trendline="lowess")
fig.show()
3、Sklearn与Plotly组合
Scikit-learn是一个流行的机器学习(ML)库,它提供了各种工具,用于创建和训练机器学习算法、特征工程、数据清理以及评估和测试模型。
这里使用Scikit-learn来分割和预处理我们的数据,并训练各种回归模型。
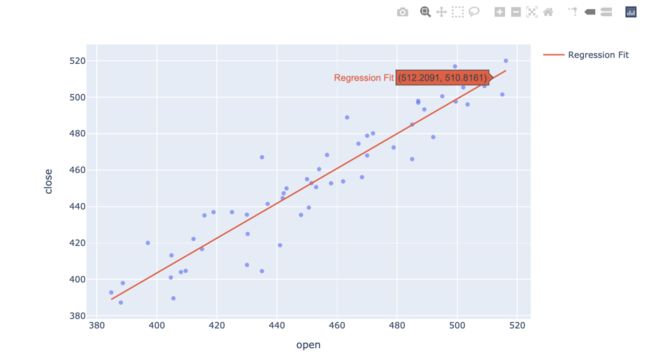
线性回归可视化
可以使用Scikit-learn的线性回归执行相同的预测。与直接用plotly.express拟合普通最小二乘回归不同,这是通过散点图和拟合线组合的方式绘制图形,这会更加灵活,除了添加普通线性回归拟合曲线,还可以组合其他线性回归曲线,即将拟合结果很好地可视化出来。
import plotly.graph_objects as go
from sklearn.linear_model import LinearRegression
X = df.open.values.reshape(-1, 1)
# 回归模型训练
model = LinearRegression()
model.fit(X, df.close)
# 生产预测点
x_range = np.linspace(X.min(), X.max(), 100)
y_range = model.predict(x_range.reshape(-1, 1))
# 图形绘制
fig = px.scatter(df, x='open', y='close', opacity=0.65)
fig.add_traces(go.Scatter(x=x_range, y=y_range, name='Regression Fit'))
fig.show()
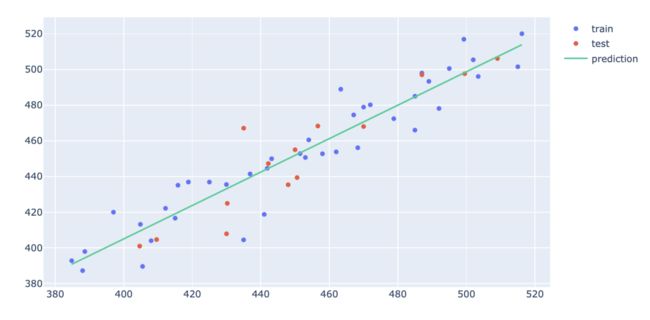
模型泛化能力可视化
利用plotly可视化查看模型泛化能力,即需要比较模型分别在训练集与测试集上的拟合状况。这里使用Scatter绘图,可以通过用不同的颜色着色训练和测试数据点,将训练集与测试集数据及拟合线绘制在同一张画布上,即可很容易地看到模型是否能很好地拟合测试数据。
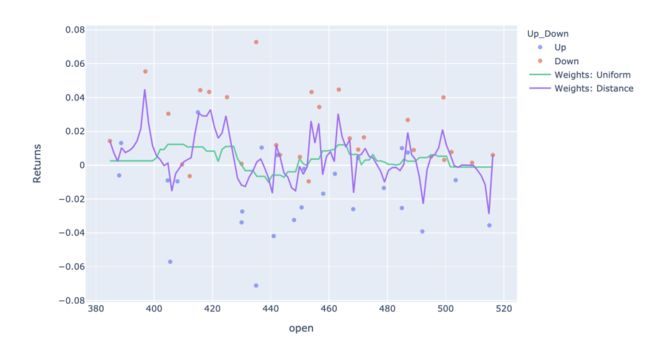
KNN回归可视化
KNN回归的原理是从训练样本中找到与新点在距离上最近的预定数量的几个点,并从这些点中预测标签。
KNN回归的一个简单的实现是计算最近邻K的数值目标的平均值。另一种方法是使用K近邻的逆距离加权平均值。
from sklearn.neighbors import KNeighborsRegressor
# 数据准备
X = df2.open.values.reshape(-1, 1)
x_range = np.linspace(X.min(), X.max(), 100)
# 模型训练,weights='distance'及weights='uniform'
knn_dist = KNeighborsRegressor(10, weights='distance')
knn_dist.fit(X, df2.Returns)
y_dist = knn_dist.predict(x_range.reshape(-1, 1))
# 绘制散点图及拟合曲线
fig = px.scatter(df2, x='open', y='Returns', color='Up_Down', opacity=0.65)
fig.add_traces(go.Scatter(x=x_range, y=y_uni, name='Weights: Uniform'))
# 'Weights: Distance'
fig.show()
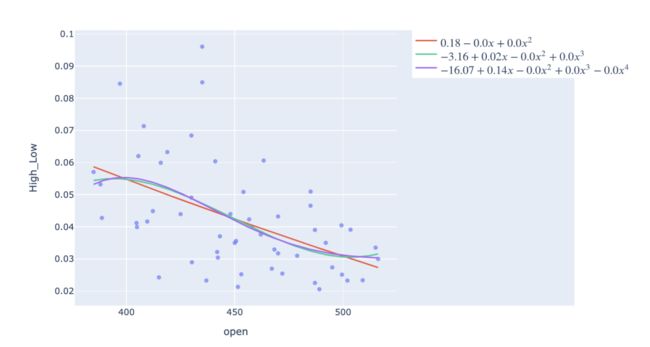
多项式回归可视化
线性回归是如何拟合直线的,而KNN可以呈现非线性的形状。除此之外,还可以通过使用scikit-learn的多项式特征为特征的n次幂拟合一个斜率,将线性回归扩展到多项式回归。
使用Plotly,只需在方程前后添加$符号,就可以在图例和标题中使用$\LaTeX$显示拟合方程,即你可以看到多项式回归拟合的系数。
# 定义图例中多项式方程函数
def format_coefs(coefs):
equation_list = [f"{coef}x^{i}" for i,
coef in enumerate(coefs)]
equation = "$" + " + ".join(equation_list) + "$"
replace_map = {"x^0": "", "x^1": "x", '+ -': '- '}
for old, new in replace_map.items():
equation = equation.replace(old, new)
return equation
# 绘制散点图
fig = px.scatter(df, x='open', y='High_Low', opacity=0.65)
# 利用循环方式绘制多项式拟合曲线
fig.add_traces(go.Scatter(x=x_range.squeeze(), y=y_poly, name=equation))
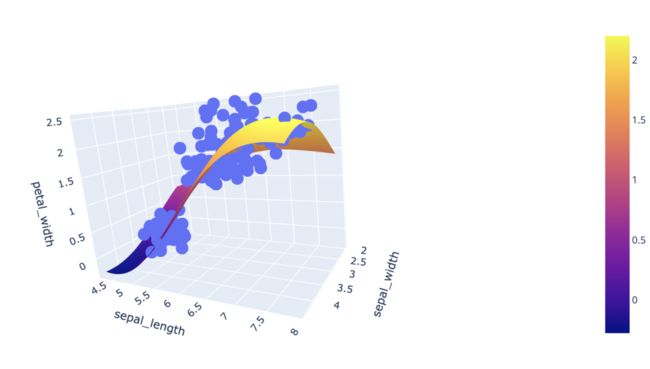
3D图绘制支持向量机决策边界
二维平面中,当类标签给出时,可以使用散点图考察两个属性将类分开的程度。即用一条直线或者更复杂的曲线,将两个属性定义的平面分成区域,每个区域包含一个类的大部分对象,则可能基于这对指定的属性构造精确的分类器,如用于二分类的逻辑回归。
而在更高维度中,即当输入数据中有多个变量时,分类器可以是支持向量机(SVM),其通过在高维空间中寻找决策边界以区分不同类别标签。如在三维空间中可以通3D图内的曲线来可视化模型的决策平面。
在Plotly中可以利用px.scatter_3d 和go.Surface绘制3D图。
from sklearn.svm import SVR
# 建立模型
model = SVR(C=1.)
model.fit(X, y)
# 使用模型预测
pred = model.predict(np.c_[xx.ravel(), yy.ravel()])
pred = pred.reshape(xx.shape)
# 绘图
fig = px.scatter_3d(df, x='sepal_length', y='sepal_width', z='petal_width')
fig.update_traces(marker=dict(size=5))
fig.add_traces(go.Surface(x=xrange, y=yrange,
z=pred, name='pred_surface'))
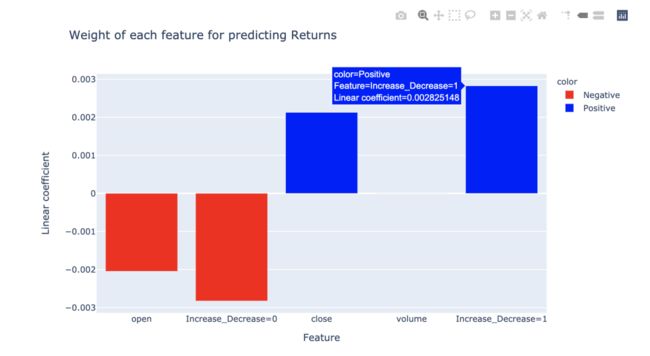
多元线性回归可视化
本节介绍用plotly可视化多元线性回归(MLR)的系数。
用一个或两个变量可视化回归是很简单的,因为可以分别用散点图和3D散点图来绘制它们。但如果有两个以上的特性,则需要找到其他方法来可视化数据。
一种方法是使用条形图。下面列子中每个条形图表示每个输入特征的线性回归模型的系数。柱状图等大小代表线性回归系数的大小,负相关与正相关分别用红色与蓝色区分,特别显目。
X = df.loc[:,['open', 'close','volume', 'Increase_Decrease']]
X = pd.get_dummies(X, columns=['Increase_Decrease'], prefix_sep='=')
y = df['Returns']
# 模型训练
model = LinearRegression()
model.fit(X, y)
# 绘制柱状图
fig = px.bar(
x=X.columns, y=model.coef_, color=colors,
color_discrete_sequence=['red', 'blue'],
labels=dict(x='Feature', y='Linear coefficient'),
title='Weight of each feature for predicting Returns'
)
fig.show()
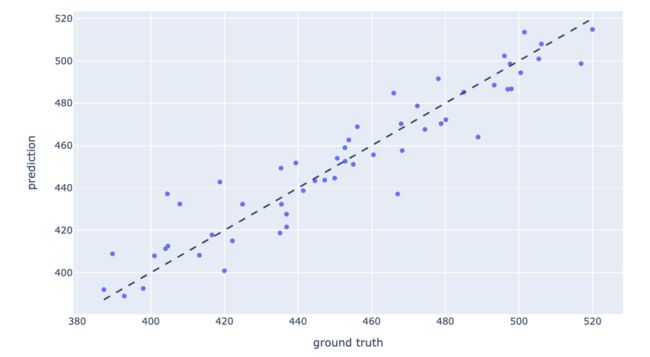
实际点与预测点的比较图
这介绍了比较预测输出与实际输出的最简单方法,即以真实值为x轴,以预测值为y值,绘制二维散点图。从图中看,若理论最优拟合(黑色斜线)附近有大部分的散点则说明模型拟合效果很好。
y_pred = model.predict(X)
# 绘制散点图
fig = px.scatter(x=y, y=y_pred,
labels={'x': 'ground truth',
'y': 'prediction'})
# 绘制理论最优拟合
fig.add_shape(
type="line", line=dict(dash='dash'),
x0=y.min(), y0=y.min(),
x1=y.max(), y1=y.max())
fig.show()
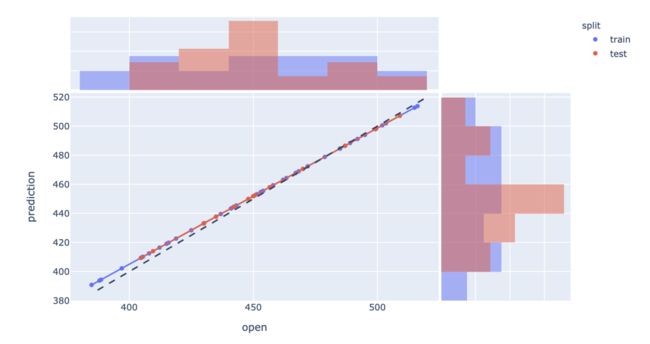
增强的预测误差分析图
通过添加边缘直方图来快速诊断模型可能存在的任何预测误差。通过将模型与理论最优拟合(黑色虚线)进行比较,内置的OLS功能可以可视化模型的泛化程度。
边缘的直方图表示在某个区间内,模型与理论最优拟合之间的误差值,不同的颜色代表不同的数据集。
model = LinearRegression()
model.fit(X_train, y_train)
df['prediction'] = model.predict(X)
# 散点图与拟合虚线
fig = px.scatter(
df, x='open', y='prediction',
marginal_x='histogram', marginal_y='histogram',
color='split', trendline='ols')
# 边缘直方图
fig.update_traces(histnorm='probability', selector={'type':'histogram'})
# 理论最优拟合 黑色虚线
fig.add_shape(
type="line", line=dict(dash='dash'),
x0=y.min(), y0=y.min(),
x1=y.max(), y1=y.max())
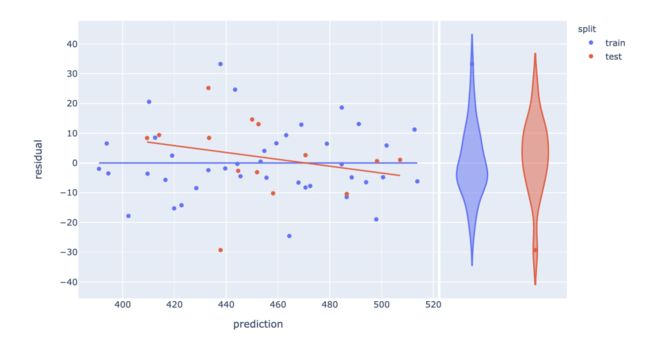
残差图
就像预测误差图一样,使用plotly很容易在几行代码中可视化预测残差。即在常规的散点图中设置预测参数trendline='ols'及预测残差参数marginal_y='violin',并以小提琴的图形展示出来。
# 模型训练
model = LinearRegression()
model.fit(X_train, y_train)
# 模型预测
df['prediction'] = model.predict(X)
df['residual'] = df['prediction'] - df['close']
# 绘制散点图和拟合线
fig = px.scatter(
df, x='prediction', y='residual',
marginal_y='violin', # 设置残差小提琴图
color='split', trendline='ols')
fig.show()
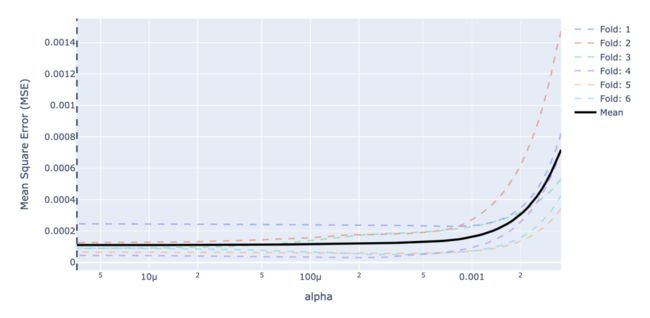
交叉验证可视化
交叉验证是将训练数据再次分配,我们以5折为例,就是说将交叉数据分成五份,每次都选取不同的数据作为验证数据。每一组不同的验证数据都会得出一个准确度,求得五组准确度的平均值,就是某个参数情况下的准确度。
Plotly可以使用Scikit-learn的LassoCV绘制交叉验证结果中各种惩罚值的结果。
from sklearn.linear_model import LassoCV
N_FOLD = 6
# 数据准备
X = df.loc[:,['open', 'close', 'Open_Close',
'High_Low', 'volume',
'Increase_Decrease']]
X = pd.get_dummies(X, columns=['Increase_Decrease'],
prefix_sep='=')
y = df['Returns']
# 模型训练
model = LassoCV(cv=N_FOLD, normalize=True)
model.fit(X, y)
mean_alphas = model.mse_path_.mean(axis=-1)
# 绘制交叉验证均方误差曲线
fig = go.Figure([
go.Scatter(
x=model.alphas_, y=model.mse_path_[:, i],
name=f"Fold: {i+1}", opacity=.5,
line=dict(dash='dash'),
hovertemplate="alpha: %{x}
MSE: %{y}")
for i in range(N_FOLD)])
# 添加交叉验证的平均均方误差
fig.add_traces(go.Scatter(
x=model.alphas_, y=mean_alphas,
name='Mean', line=dict(color='black', width=3),
hovertemplate="alpha: %{x}
MSE: %{y}",))
fig.show()
基于决策树的网格搜索可视化
Scikit-learn机器学习中的GridSearchCV,即GridSearch和CV,网格搜索和交叉验证。
网格搜索,搜索的是参数,即在指定的参数范围内,按步长依次调整参数,利用调整的参数训练学习器,从所有的参数中找到在验证集上精度最高的参数,这其实是一个训练和比较的过程。
Plotly中运用px.density_heatmap 和 px.box,在DecisionTreeRegressor上将网格搜索过程可视化。
网格搜索调参
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeRegressor
N_FOLD = 6
X = df[['open', 'volume']]
y = df['close']
# 定义与训练网格搜索
model = DecisionTreeRegressor()
param_grid = {
'criterion': ['mse', 'friedman_mse', 'mae'],
'max_depth': range(2, 5)}
grid = GridSearchCV(model, param_grid, cv=N_FOLD)
grid.fit(X, y)
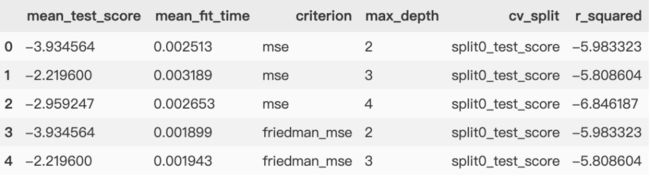
grid_df = pd.DataFrame(grid.cv_results_)
# 将网格的宽格式转换为长格式
单个函数调用来绘制每个图形
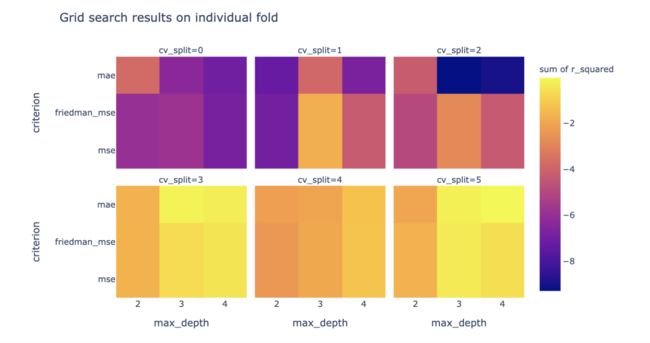
第一个图显示了如何在单个分割(使用facet分组)上可视化每个模型参数的分数。
每个大块代表不同数据分割下,不同网格参数的R方和。而其中每个小块代表相同数据分割下,网格参数:'criterion'与'max_depth'在不同取值组合下的R方和。
fig_hmap = px.density_heatmap(
melted, x="max_depth", y='criterion',
histfunc="sum", z="r_squared",
title='Grid search results on individual fold',
hover_data=['mean_fit_time'],
facet_col="cv_split", facet_col_wrap=3,
labels={'mean_test_score': "mean_r_squared"})
fig_hmap.show()
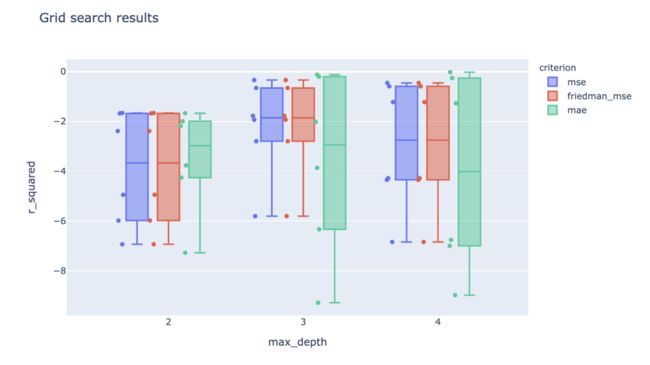
第二个图汇总了所有分割的结果,每个盒子代表一个单一的模型。三组盒子代表三个不同的树深度'max_depth',每组中不同颜色的盒子代表不同的评价标准'criterion'。
fig_box = px.box(
melted, x='max_depth', y='r_squared',
title='Grid search results ',
hover_data=['mean_fit_time'],
points='all',
color="criterion",
hover_name='cv_split',
labels={'mean_test_score': "mean_r_squared"})
fig_box.show()
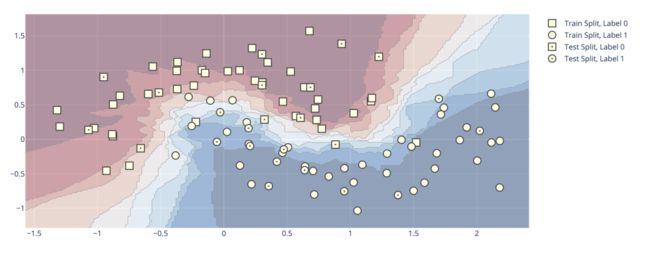
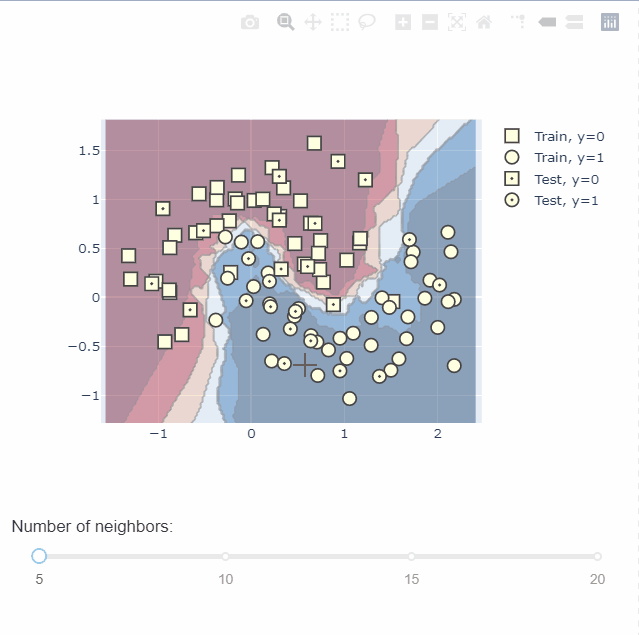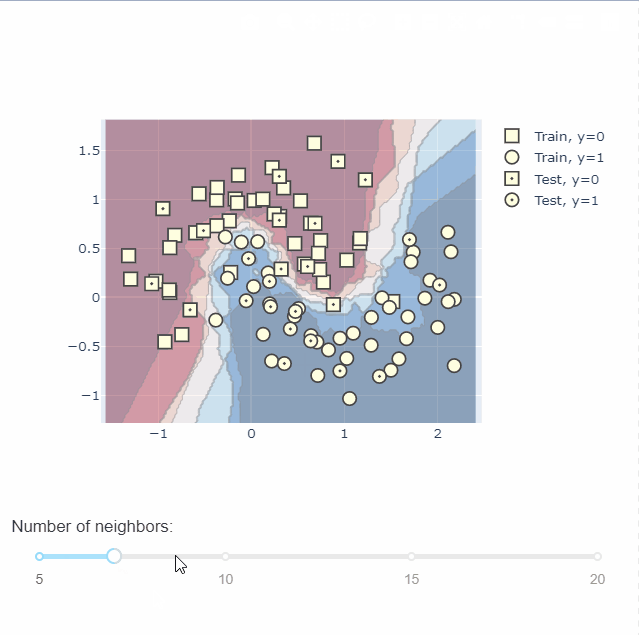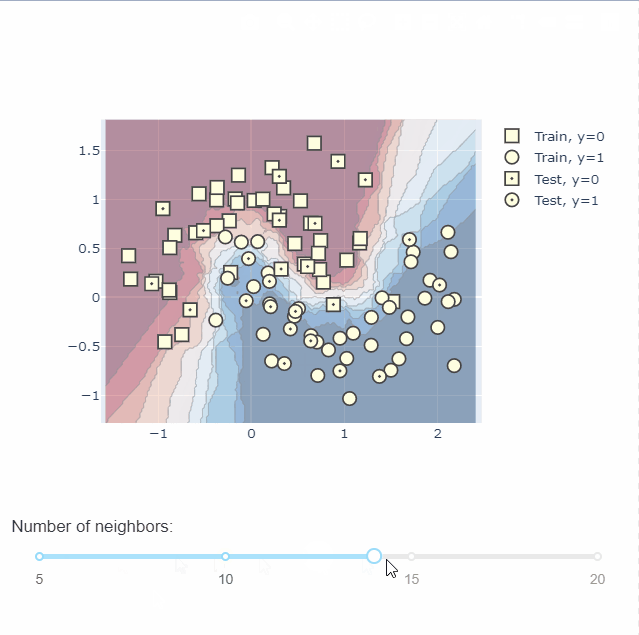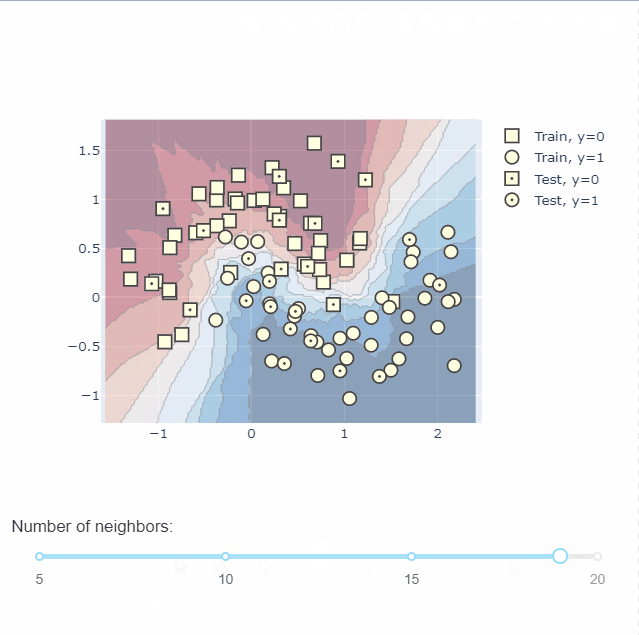
KNN分类可视化
训练一个 K-Nearest Neighbors 分类器,首先模型记录每个训练样本的标签。然后每当给它一个新样本时,它就会从训练集中找k个最接近的样本来找到对应的标签,然后做投票,看看这个区域内,哪个类别标签数量多,以确定标签值并把它赋给新样本。
在图中,将所有负标签显示为正方形,正标签显示为圆形。我们通过在测试数据中心添加一个点来区分训练集和测试集。
通过plotly中的dash还可以绘制交互图,不同参数下不同的决策边界,无疑给我们理解模型提供了一个很好的帮手。具体绘图过程可以到官网查看,这里不做过多的介绍。
模型评价可视化
这里的模型评价主要针对分类模型,回归模型用拟合误差、拟合残差等可以评价回归模型的优劣,前面已经介绍过了。此处主要是将模型的预测概率、模型效果可视化,如假正率真正率曲线图、绘制ROC曲线图等。
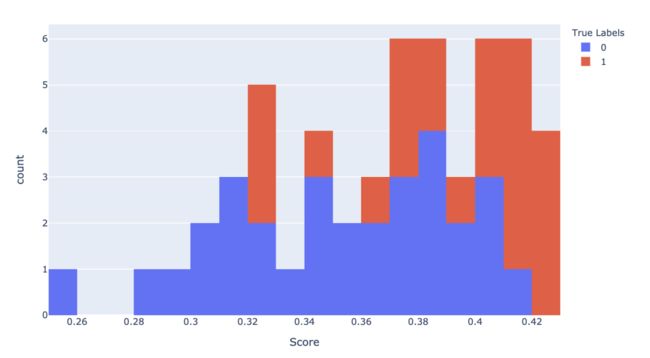
与真实标签相比的分数直方图
from sklearn.metrics import roc_curve, auc
# 二分类逻辑回归建模
model = LogisticRegression()
model.fit(X, y)
# 模型预测概率
y_score = model.predict_proba(X)[:, 1]
# 绘制预测概率直方图
fig_hist = px.histogram(
x=y_score, color=y, nbins=30,
labels=dict(color='True Labels', x='Score'))
fig_hist.show()
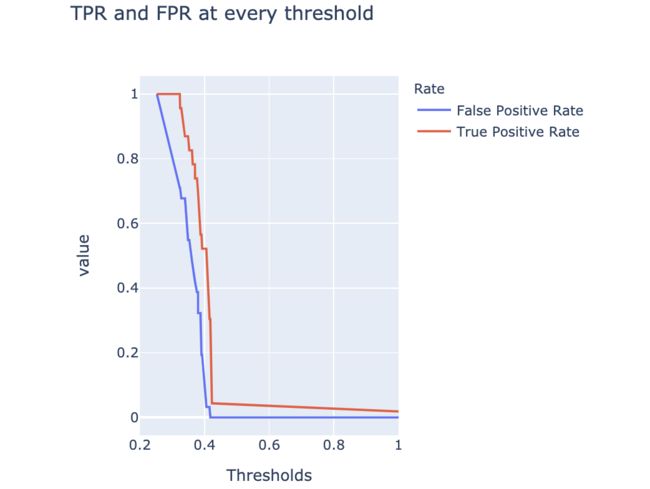
在不同的阈值下评估模型性能
# 计算ROC曲线各个值
fpr, tpr, thresholds = roc_curve(y, y_score)
# 建立阈值数据框
df = pd.DataFrame({
'False Positive Rate': fpr,
'True Positive Rate': tpr}
, index=thresholds)
df.index.name = "Thresholds"
df.columns.name = "Rate"
# 绘制折线图
fig_thresh = px.line(
df, title='TPR and FPR at every threshold',
width=500, height=500)
# 设置x/y轴
fig_thresh.update_yaxes(scaleanchor="x", scaleratio=1)
fig_thresh.update_xaxes(range=[0.2, 1], constrain='domain')
fig_thresh.show()
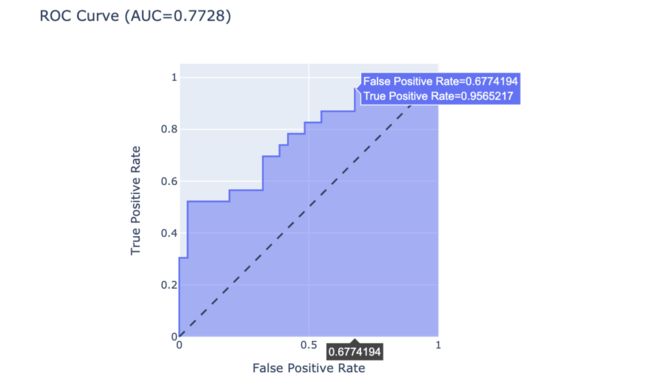
# 绘制面积图
fig = px.area(
x=fpr, y=tpr,
title=f'ROC Curve (AUC={auc(fpr, tpr):.4f})',
labels=dict(x='False Positive Rate',
y='True Positive Rate'),
width=700, height=500)
# 添加理论线 黑色虚线
fig.add_shape(
type='line', line=dict(dash='dash'),
x0=0, x1=1, y0=0, y1=1)
# 更新图表样式
fig.update_yaxes(scaleanchor="x", scaleratio=1)
fig.update_xaxes(constrain='domain')
fig.show()