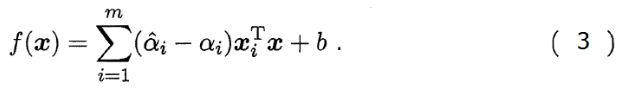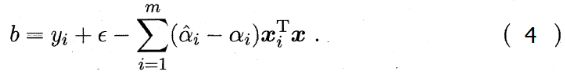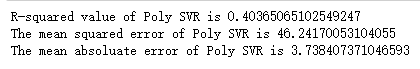python机器学习——支持向量机回归与波士顿房价案例

一、从传统回归模型到支持向量回归模型

我们前面讨论过支持向量机分类模型，在前文的基础上我们来考虑回归问题。给定训练样本 D = {(x1,y1),(x2,y2),…,(xm,ym)}， yi∈R，希望学得一个形如

的回归模型，使得 f(x) 与 y 尽可能接近，ω 和 b 是待确定的模型参数。

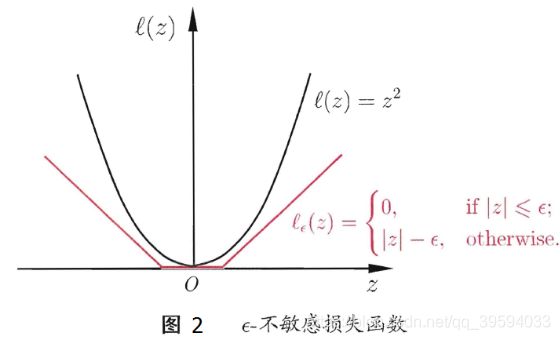
对样本(x,y)，传统回归模型通常直接基于模型输出 f(x) 与真实输出 y 之间的差别来计算损失，当且仅当 f(x) 与 y 完全相同时，损失才为 0。与此不同，支持向量回归(Support Vector Regression，简称 SVR)假设我们能容忍 f(x) 与 y 之间最多有 ε 的偏差，即当 |f(x)-y| > ε时才计算损失。

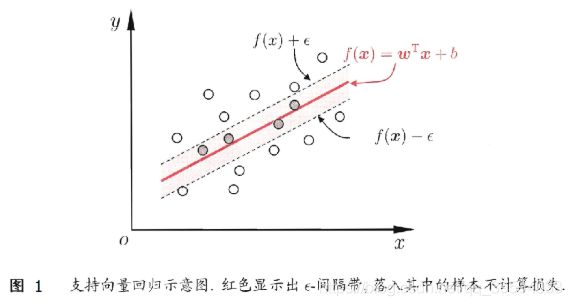
如图 1 所示，这相当于以 f(x) 为中心，构建了一个宽度为 2ε的间隔带，若训练样本落入此间隔带，则认为是被预测正确的。

于是，SVR 问题可形式化为如下优化问题 ：

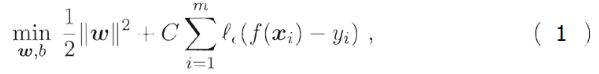
其中 C 为正则化常数，lε 是图2所示的ε-不敏感损失(ε-insensitive loss)函数

引入松弛变量 ζi，可将公式(1)改写为

使用拉格朗日乘子法求解得，SVR 的解形如

能使公式(3)中的

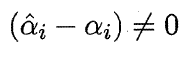
的样本即为 SVR 的支持向量，它必落在ε-间隔带之外。显然，SVR 的支持向量仅是训练样本的一部分，即其解仍具有稀疏性。

理论上，可任选满足 0<αi< C 样本通过

求得 b 。实践中常采用一种更稳健(是指控制系统在一定（结构，大小）的参数摄动下，维持其它某些性能的特性)的方法:选取多个(或所有)满足条件的样本求解 b 后取平均值。

二、核函数

支持向量机回归广泛使用核函数，其目的是通过改变原数据维度，从而可以在新的空间进行线性回归。

当输入样本线性不可分的话，采取的方法是通过 Φ:X↦F 函数映射将输入样本映射到另外一个高维空间并使其线性可分，这个过程可由下图表示：

完成映射之后，原来需要计算,现在转化为需要计算<Φ(xi),Φ(xj)>，这便是核函数的思路和原理。

下面是核函数的具体定义：

核是一个函数 K ，对于所有的 x,x′∈X 满足，K =<Φ(x),Φ( x′)> ，这里的 Φ 为从 X 到内积特征空间 F 的映射。

三、常用的几种核函数

四、SVM 算法的优缺点

主要优点：

(1) 解决高维特征的分类问题和回归问题很有效,在特征维度大于样本数时依然有很好的效果。

(2) 仅仅使用一部分支持向量来做超平面的决策，无需依赖全部数据。

(3) 有大量的核函数可以使用，从而可以很灵活的来解决各种非线性的分类回归问题。

(4) 样本量不是海量数据的时候，分类准确率高，泛化能力强。

主要缺点：

(1) 如果特征维度远远大于样本数，则 SVM 表现一般。

(2) SVM 在样本量非常大，核函数映射维度非常高时，计算量过大，不太适合使用。

(3)非线性问题的核函数的选择没有通用标准，难以选择一个合适的核函数。

(4)SVM 对缺失数据敏感。

五、建模实例

（1）导入数据

# 从 sklearn.datasets 导入波士顿房价数据读取器。
from sklearn.datasets import load_boston
# 从读取房价数据存储在变量 boston 中。
boston = load_boston()

（2）划分训练集测试集

# 从sklearn.cross_validation 导入数据分割器。
from sklearn.model_selection import train_test_split
X = boston.data
y = boston.target
# 随机采样 25% 的数据构建测试样本，其余作为训练样本。
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)

（3）数据标准化

使用线性核函数配置的支持向量机

# 从 sklearn.svm 中导入支持向量机（回归）模型。
from sklearn.svm import SVR
# 使用线性核函数配置的支持向量机进行回归训练，并且对测试样本进行预测。
linear_svr = SVR(kernel='linear')
linear_svr.fit(X_train, y_train)
linear_svr_y_predict = linear_svr.predict(X_test)

使用多项式核函数配置的支持向量机

# 使用多项式核函数配置的支持向量机进行回归训练，并且对测试样本进行预测。
poly_svr = SVR(kernel='poly')
poly_svr.fit(X_train, y_train)
poly_svr_y_predict = poly_svr.predict(X_test)

使用径向基核函数配置的支持向量机

# 使用径向基核函数配置的支持向量机进行回归训练，并且对测试样本进行预测。
rbf_svr = SVR(kernel='rbf')
rbf_svr.fit(X_train, y_train)
rbf_svr_y_predict = rbf_svr.predict(X_test)

from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
print('R-squared value of linear SVR is', linear_svr.score(X_test, y_test))
print('The mean squared error of linear SVR is', mean_squared_error(
    ss_y.inverse_transform(y_test), ss_y.inverse_transform(linear_svr_y_predict)))
print('The mean absoluate error of linear SVR is', mean_absolute_error(
    ss_y.inverse_transform(y_test), ss_y.inverse_transform(linear_svr_y_predict)))

print('R-squared value of Poly SVR is', poly_svr.score(X_test, y_test))
print('The mean squared error of Poly SVR is', mean_squared_error(
    ss_y.inverse_transform(y_test), ss_y.inverse_transform(poly_svr_y_predict)))
print('The mean absoluate error of Poly SVR is', mean_absolute_error(
    ss_y.inverse_transform(y_test), ss_y.inverse_transform(poly_svr_y_predict)))

print('R-squared value of RBF SVR is', rbf_svr.score(X_test, y_test))
print('The mean squared error of RBF SVR is', mean_squared_error(
    ss_y.inverse_transform(y_test), ss_y.inverse_transform(rbf_svr_y_predict)))
print('The mean absoluate error of RBF SVR is', mean_absolute_error(
    ss_y.inverse_transform(y_test), ss_y.inverse_transform(rbf_svr_y_predict)))

性能输出显示：不同核函数的配置下模型在相同测试集上，存在着非常大的性能差异。其中高斯核(Rbf)函数对特征进行非线性映射后，回归性能最佳。

参考文献：

[1] 周志华. 机器学习[M]. 清华大学出版社, 北京, 2016.
[2] 范淼，李超.Python 机器学习及实践[M].清华大学出版社, 北京, 2016.