【Homography Estimation】《Deep Image Homography Estimation》
arXiv-2016
文章目录
- 1 Background and Motivation
- 2 Related Work
- 3 Advantages / Contributions
- 4 Method
- 5 Experiments
-
- 5.1 Datasets
- 5.2 Experiments
- 6 Conclusion
1 Background and Motivation
用卷积直接回归单应性矩阵(transformation estimation,homography estimation),8个自由度
The homography is an essential part of monocular SLAM systems in scenarios such as:
- Rotation only movements
- Planar scenes
- Scenes in which objects are very far from the viewer
2 Related Work
无
3 Advantages / Contributions
利用卷积神经网络学四个点的偏移来进行 Homography Estimation
4 Method
(1)The 4-point homography parameterization
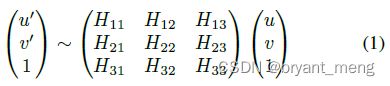
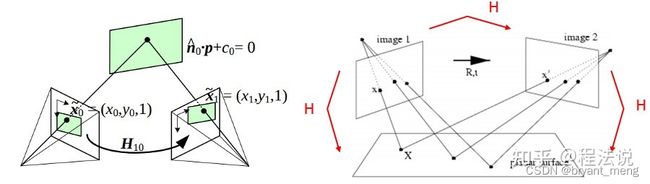
单应性矩阵把图 ( u , v ) (u,v) (u,v) 映射成了 ( u ′ , v ′ ) (u',v') (u′,v′)
H11 H12 H21 H22 与旋转有关,H13 H23 和平移有关
Balancing the rotational and translational terms as part of an optimization problem is difficult
单应性矩阵中 9个参数相互组合有实际意义,没有完全解耦干净, 9 个参数共 8 个自由度,作者直接改学图 ( u , v ) (u,v) (u,v) 映射成了 ( u ′ , v ′ ) (u',v') (u′,v′) 的 4 个坐标的偏移(传统方法也有这么干的)
学到 4 个坐标的偏移后,利用 OpenCV. 的 getPerspectiveTransform() 方法就可以计算出单应性矩阵了
输入来自源图像的 4 个点和加上偏移的 4 个新点,getPerspectiveTransform 将返回一个(3,3) 矩阵
(2)Data Generation for Homography Estimation
applying random projective transformations to a large dataset(MS COCO)


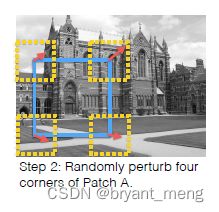
原图上随机选个矩形区域 p,四个顶点随机偏移,根据四个点前后坐标,计算出单应性矩阵,然后把单应性矩阵作用到原图生成新的图,新的图对应的 p 区域 p’ 和 原图的 p 联合送入网络学习原图四个顶点坐标的偏移(step2)进而求出 H A B H^{AB} HAB
import cv2
import numpy as np
im1 = cv2.imread('left.jpg')
im2 = cv2.imread('right.jpg')
src_points = np.array([[581, 297], [1053, 173], [1041, 895], [558, 827]])
dst_points = np.array([[571, 257], [963, 333], [965, 801], [557, 827]])
H, _ = cv2.findHomography(src_points, dst_points)
h, w = im2.shape[:2]
im2_warp = cv2.warpPerspective(im2, H, (w, h))
Managing the training image generation pipeline gives us full control over the kinds of visual effects we want to model
比如加模糊(robust to motion blur),加遮挡(robust to occlusions)
VGG-style
输入两个单通道 concat, 128 ∗ 128 ∗ 2 128*128*2 128∗128∗2
( I A , I B , H A B ) (I_A,I_B,H^{AB}) (IA,IB,HAB) from real images, seemingly infinite dataset
回归网络 the real-valued homography parameters,只有输出结果,无法反应置信度
分类网络 a distribution over quantized homographies and can be used to determine the confidence of an estimated homography
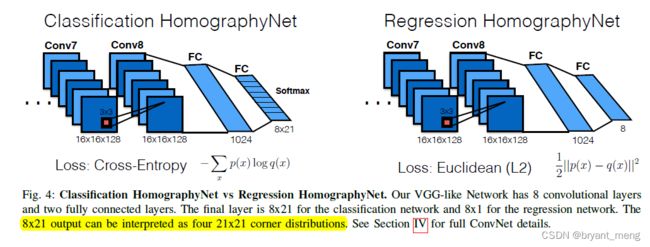

把偏移量化输出到 21 个空间(盲猜一手 5x5 去掉 4 个顶点,25-4 = 21)
When evaluating the Classification HomographyNet, the corner displacement with the highest confidence is chosen.
5 Experiments
5.1 Datasets
warped MS-COCO images(resized to 320x240 and converted to grayscale)
训练集
产生 500,000 pairs 数据,patch 大小 128x128(蓝色实框区域),随机偏移的范围 ρ \rho ρ 设置为了 32(虚线黄色框范围)
5000,resize 成 640x480,patch 大小为 256x256 区域(主要是方便对比传统方法,作者对比的传统方法中 patch 的区域为 128x128 的话难找到特征点)

评价指标,预测出的4 个坐标 和 GT 的均方差
5.2 Experiments
6 Conclusion
作者 We hope that more geometric problems in vision will be tackled using learning paradigms.
节选一些优秀的博文
(1)【相机标定04】单应矩阵的作用
(2)单应性Homograph估计:从传统算法到深度学习
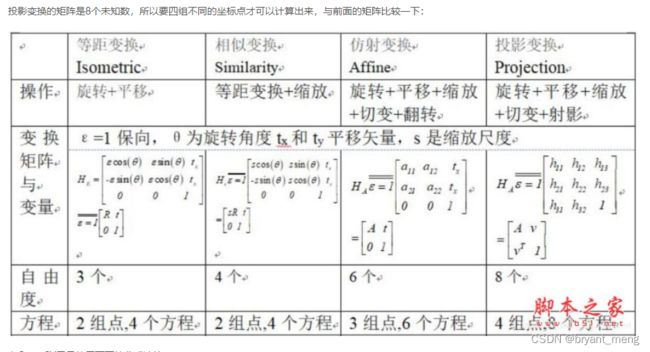
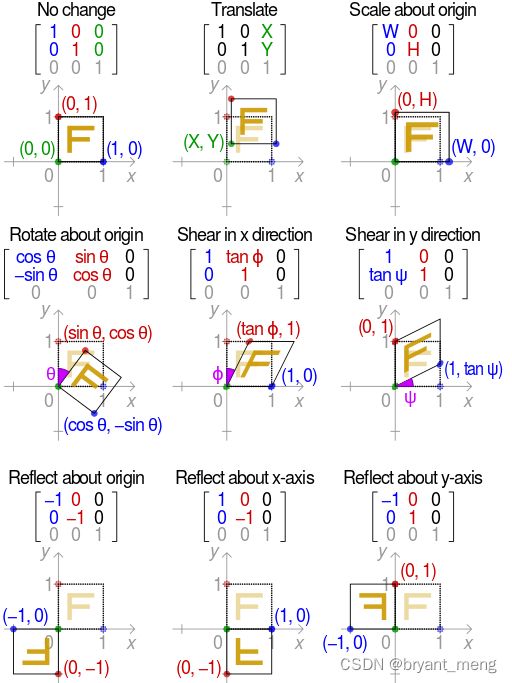
刚体变换:平移+旋转,只改变物体位置,不改变物体形状
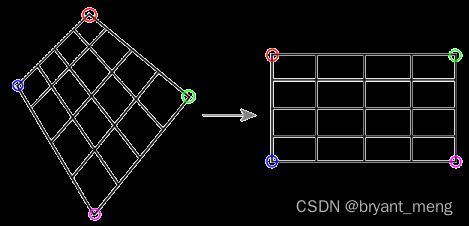
仿射变换:改变物体位置和形状,但是保持“平直性”(原来平行的边依然平行)
投影变换:彻底改变物体位置和形状
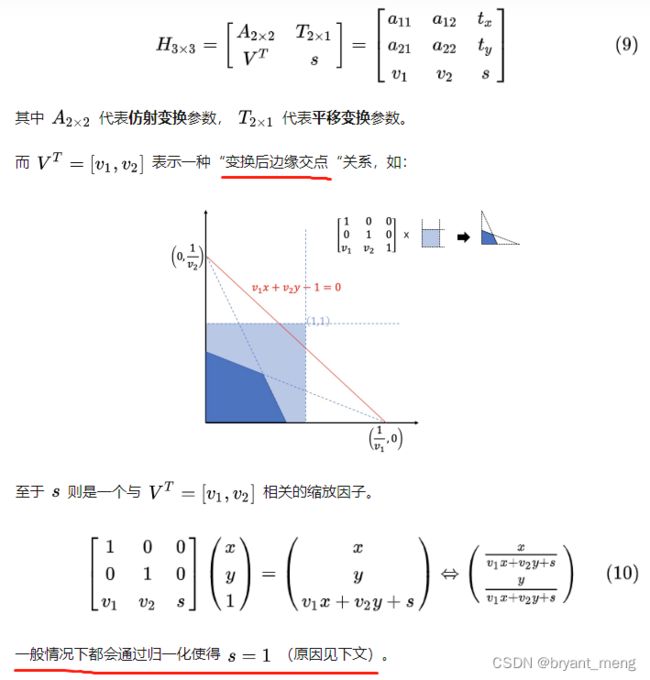
为啥 3x3 矩阵只有 8 个自由度???(单应性Homograph估计:从传统算法到深度学习)
(3)仿射变换和单应矩阵有什么本质的区别?
我就看看看看的回答
gamemonkey的回答
(4)python在OpenCV里实现投影变换效果
(5)仿射变换及其变换矩阵的理解
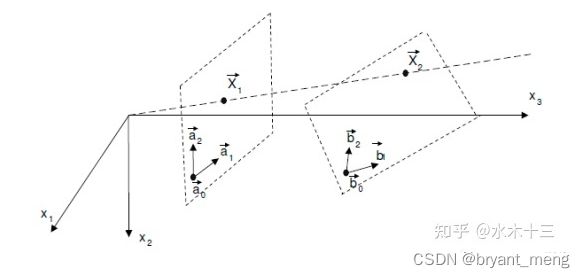
(6)推导四对对应点单应矩阵的计算公式? - 水木十三的回答 - 知乎
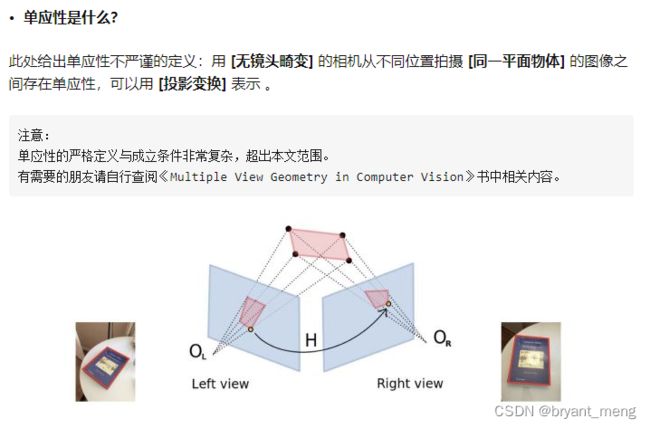
单应性矩阵主要用来解决两个问题,
一是表述真实世界中一个平面与对应它图像的透视变换。
二是通过透视变换实现图像从一种视图变换到另外一种视图。