用python实现遗传算法

Hello，大家好！最近事情比较多，一个月没有写公众号了，但也积累了些不错的内容可以分享，今天就给大家介绍的是遗传算法，并用python加以实现。

在遗传算法的学习过程中，在CSDN上看到一篇已有人分享的python代码，因此直接借鉴过来，并结合《数学建模与数学实验》进行补充。（电子书和原博主链接见文末）

遗传算法介绍

遗传算法（Genetic Algorithm），是由美国的J.Holland教授于1975年首先提出的，是受达尔文的进化论的启发，借鉴生物进化过程而提出的一种启发式搜索算法。

生存竞争，适者生存：对环境适应度高的个体参与繁殖的机会比较多，后代就会越来越多。适应度低的个体参与繁殖的机会比较少，后代就会越来越少。

简单来说就是一个繁殖的过程，会发生基因交叉（Crossover），基因突变（Mutation），适应度（Fitness）低的个体会被逐步淘汰，而适应度高的个体会越来越多。

操作思路

初始化

初始化进化代数计数器t←0，最大进化代数T（一般100_{500），初始化变异概率α（一般0.0001}0.2）、交叉概率β（一般0.4_{0.99），随机生成M个（一般20}100）个体作为初始群体P(t)。

编码

遗传算法中，首要问题就是如何对解进行编码（解的形式），编码影响到交叉、变异等运算，很大程度上决定了遗传算法的效率。

​ 二进制编码：每个基因值为符号0和1所组成的二进制数；

​ 格雷编码：与二进制编码类似，连续两个整数所对应编码仅一码之差；

​ 实数编码：每个基因值用某一范围内的一个实数来表示；

​ 符号编码：染色体编码串中的基因值取自一个无数值含义，而只有代码含义的符号集。

个体评价

计算P(t)中各个个体的适应度值。适应度函数：也称评价函数，是根据目标函数确定的用于区分群体中个体好坏的标准，适应度函数值的大小是对个体的优胜劣汰的依据。

选择

选择运算的作用是对个体进行优胜劣汰：从父代群体中选取一些适应度高个体遗传到下一代群体中。

​ 轮盘赌法：又称比例选择算子，个体i被选中的概率Pi与其适应度成正比：
$$p_i=\frac{f_i}{{\sum }_{i=1}^N{f}_i}$$
​ 两两竞争：从父代中随机地选取两个个体，比较适应度值，保存优秀个体，淘汰较差的个体

​ 排序选择：根据各个体的适应度大小进行排序，然后基于所排序号进行选择。

交叉

是指对两个相互配对的染色体，依据交叉概率按某种方式相互交换其部分基因，从而形成两个新的个体。

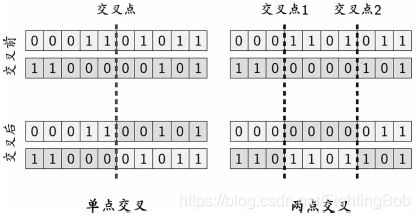
变异

是对群体中的个体的某些基因座上的基因值作变动，模拟生物在繁殖过程，新产生的染色体中的基因会以一定的概率出错。

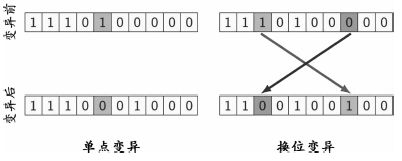
Python实现

初始化

DNA_SIZE = 24
POP_SIZE = 100
CROSSOVER_RATE = 0.8
MUTATION_RATE = 0.005
N_GENERATIONS = 100

编码

在遗传算法中，最常用的就是二进制编码，我们可以利用np.random.randint()来实现：

pop = np.random.randint(2, size = (POP_SIZE, DNA_SIZE*2))

参数说明：

numpy.random.randint(low, high=None, size=None, dtype=‘l’)

1、low：生成的数值最低要大于等于low；当hign = None时，生成的数值要在[0, low)区间内；

2、high：如果使用这个值，则生成的数值在[low, high)区间；

3、size：输出随机数的尺寸。默认是None的，仅仅返回满足要求的单一随机数；

4、dtype：想要输出的格式。如int64、int等等。

一般来说DNA长度越长，所包含的信息越多，结果就越精确，当然还得具体问题具体分析。

虽然二进制编码实现容易，便于操作，但是对于一些连续函数的优化问题，由于其随机性使得其局部搜索能力较差，当解迫近于最优解后，由于其变异后表现型变化很大，不连续，所以会远离最优解，达不到稳定。

格雷码的好处就在于能够提高遗传算法的局部搜索能力，相比二进制精度更高。

因此，给大家介绍如何把二进制转化为格雷码（原理大家自行查阅）：

def BToG(pop):
    pop_g = []
    for i in pop:
        new = [i[0]]
        for j in range(1,len(i)):
            new.append(new[j-1]^i[j])
		pop_g.append(new)
	return np.array(pop_g)

参数说明：

“^”是按位异或运算符：当两对应的二进位相异时，结果为1，相同结果为0。

当然，对其进行编码后还需要再将其解码回二进制：

def jiema(pop_g):
    
    pop = []
    for i in pop_g:
       new = [i[0]]
       for j in range(1,len(i)):
         if i[j] == 0:
           new.append(new[j-1])
         else:
           if new[j-1] == 0:
             new.append(1)
           else:
             new.append(0)
      pop.append(new)
    return np.array(pop)

不同的编码，后续所对应的变换和突变也会有所不同，因为格雷码和二进制码比较相似，因此在这就先介绍这两种，其它编码欢迎加好友一起探讨学习。

个体评价

通常评价函数可以由目标函数直接或间接改造得到。比如，目标函数或目标函数的倒数/相反数经常被直接用作适应度函数。一般情况下，适应度是非负的，并且总是希望适应度越大越好。比较好的适应度函数应单值、连续、非负、最大化。

def get_fitness(pop): 

  x1, x2 = translateDNA(pop)

  pred = F(x1, x2)

  return (pred - np.min(pred))

注：

translateDNA()是自定义的函数，用于将二进制码转换为数值，在测试部分会提到；F()是目标函数。

该评价函数是为了评价最大值的适应度，减去最小的结果是为了避免出现负数的情况；同理，如果我们想要最小值的适应度，就可以改成np.max (pred)-pred即可。

选择

两两竞争和排序选择都容易产生局部最优解的情况，因此遗传算法中更多使用的是轮盘赌法：

def select(pop, fitness):
    idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
                           p=(fitness)/(fitness.sum()))
	return pop[idx]

参数说明：

numpy.random.choice(a, size=None, replace=True, p=None)

1、从a(只要是ndarray都可以，但必须是一维的)中随机抽取数字，并组成指定大小(size)的数组；

2、replace:True表示可以取相同数字，False表示不可以取相同数字；

3、数组p：与数组a相对应，表示取数组a中每个元素的概率，默认为选取每个元素的概率相同。

变异

def mutation(child, MUTATION_RATE=0.003):
   if np.random.rand() < MUTATION_RATE:
   	mutate_point = np.random.randint(0, DNA_SIZE)
   	child[mutate_point] = child[mutate_point]^1

交叉：单点交叉&两点交叉

单点交叉：

def crossover_and_mutation(pop, CROSSOVER_RATE = 0.8):
    new_pop = []
    for father in pop: 
        child = father
        if np.random.rand() < CROSSOVER_RATE:
            mother = pop[np.random.randint(POP_SIZE)]
            cross_points = np.random.randint(low=0, high=DNA_SIZE*2)
            child[cross_points:] = mother[cross_points:] 
            mutation(child) 
            new_pop.append(child)
	return new_pop

两点交叉：

def crossover_and_mutation(pop, CROSSOVER_RATE = 0.8):
    new_pop = []
    for father in pop: 
        child = father
        if np.random.rand() < CROSSOVER_RATE: 
            mother = pop[np.random.randint(POP_SIZE)]
            cross_points_1 = np.random.randint(low=0, high=DNA_SIZE*2)
            cross_points_2 = np.random.randint(low= cross_points_1, high=DNA_SIZE*2)
            child[cross_points_1: cross_points_2] = mother[cross_points_1:cross_points_2]
            mutation(child)
            new_pop.append(child)
    return new_pop

到此，遗传算法中所有的步骤我们均已实现，后面我们就以原博主所用的例子将所有步骤串起来，来进行测试。（此次测试与原博主不同的是采用格雷编码以及两点交叉遗传）

我们再拿原博主的代码跑一次做个对比。

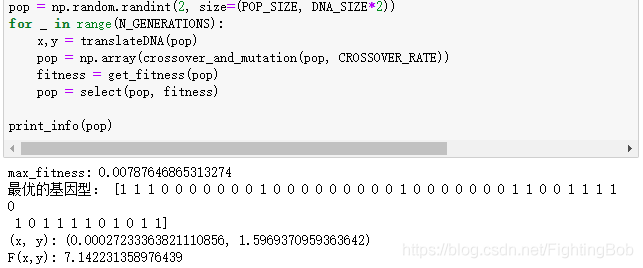
从结果中可以看出，虽然我们用了新的编码和遗传形式进行计算，但结果并没有原博主的好，所以具体问题具体分析，用算法前得多加思考，多加尝试。

参考资料

1、https://blog.csdn.net/u014484715/article/details/40046307

2、《数学建模与数学实验》

获得代码

以下是我的个人公众号，本文完整代码已上传，关注公众号回复“遗传算法”，即可获得，回复“《数学建模与数学实验》”（注意要打“《》”），即可获得该书的电子版，谢谢大家支持。