遗传算法原理及其python实现
遗传算法简介
遗传算法(Genetic Algorithm,GA)最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果
达尔文进化论的原理概括总结如下:
- 变异:种群中单个样本的特征(性状,属性)可能会有所不同,这导致了样本彼此之间有一定程度的差异
- 遗传:某些特征可以遗传给其后代。导致后代与双亲样本具有一定程度的相似性
- 选择:种群通常在给定的环境中争夺资源。更适应环境的个体在生存方面更具优势,因此会产生更多的后代
遗传算法的基本概念
由于遗传算法是由进化论和遗传学机理而产生的搜索算法,所以在这个算法中会用到一些生物遗传学知识,下面是我们将会用一些术语:
由于遗传算法是由进化论和遗传学机理而产生的搜索算法,所以在这个算法中会用到一些生物遗传学知识,下面是我们将会用一些术语:
- 基因型 (Genotype) :在自然界中,通过基因型表征繁殖,繁殖和突变,基因型是组成染色体的一组基因的集合。
- 种群 (Population): 可行解域,根据适应度函数选择的一组解
- 染色体(Chromosome): 对每个可行解的编码
- 变异(Mutation): 突变操作的目的是定期随机更新种群,将新模式引入染色体,并鼓励在解空间的未知区域中进行搜索。
- 选择 (Selection): 保留适应度函数的函数值优的解
- 交叉 (CrossOver): 将两个可行解内的组分随机交叉,产生新解
- 适应性(Fitness): 适应度函数的函数值
算法流程图
python实践
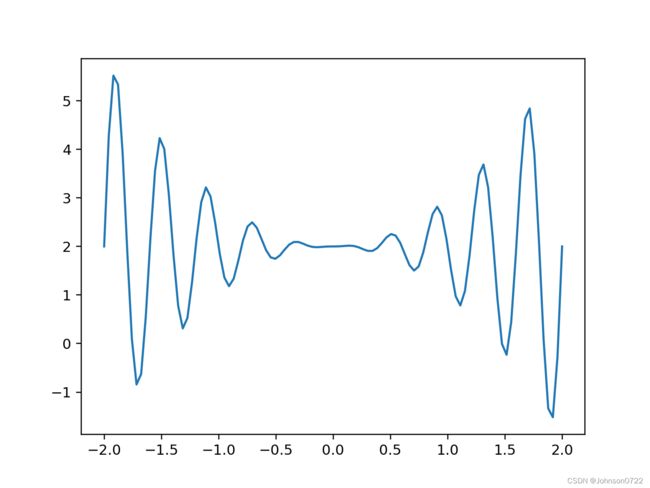
我们来考虑下面这个优化问题,求解
f ( x ) = x 2 ∗ s i n ( 5 π x ) + 2 f(x) = x^2 * sin(5 \pi x) + 2 f(x)=x2∗sin(5πx)+2
在区间[-2, 2]上的最大值。很多单点优化的方法(梯度下降等)就不适合,可能会陷入局部最优的情况,这种情况下就可以用遗传算法(Genetic Algorithm。
问题定义
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def f(x):
return x**2 * np.sin(5*np.pi*x) + 2
x = np.linspace(-2, 2, 100)
plt.plot(x, f(x))
初始化原始种群
遗传算法可以同时优化一批解 (种群), 我们在[-2, 2]的区间内随机生成10个点作为我们的初始种群
np.random.seed(0)
def init_population(size):
return np.random.uniform(low=-2, high=2, size=size)
population = init_population(10)
plt.plot(x, f(x))
plt.plot(population, f(population), '*')
plt.show()
染色体编码和解码
解空间中的解在遗传算法中的表示形式。从问题的解(solution)到基因型的映射称为编码,即把一个问题的可行解从其解空间转换到遗传算法的搜索空间的转换方法。遗传算法在进行搜索之前先将解空间的解表示成遗传算法的基因型串(也就是染色体)结构数据,这些串结构数据的不同组合就构成了不同的点。
常见的编码方法有二进制编码、格雷码编码、 浮点数编码、各参数级联编码、多参数交叉编码等。
简单起见,我们使用二进制编码。为了能编码浮点数,需要扩大倍数转成整数。
def encode(population, scale=1e4, _min=-2, bin_len=15):
_scaled_population = (population - _min) * scale
chroms = np.array([np.binary_repr(x, width=bin_len) for x in _scaled_population.astype(int)])
return chroms
def decode(chroms, _min=-2, scale=1e4):
res = np.array([(int(x, base=2)/scale) for x in chroms])
res += _min
return res
fitness = f(population)
chroms = encode(population)
print(population)
print(decode(encode(population)))
print(fitness)
>>>
[ 0.1953 0.8608 0.4111 0.1795 -0.3054 0.5836 -0.2497 1.5671 1.8547 -0.4662]
[ 0.1953 0.8608 0.4111 0.1795 -0.3054 0.5836 -0.2497 1.5671 1.8547 -0.4662]
[ 2.00281338 2.60488832 2.02931805 2.01019697 2.09293383 2.0867721
2.04387992 0.78660371 -0.60517298 1.81257758]
选择
选择操作从旧群体中以一定概率选择优良个体组成新的种群,以繁殖得到下一代个体。个体被选中的概率跟适应度值有关,个体适应度值越高,被选中的概率越大,常用的选择算法为轮盘赌算法。若种群数位 M M M, 个体 i i i的适应度为 f i f_i fi,则个体 i i i被选中的概率为:
p i = f i ∑ k = 1 M f k p_i = \frac{f_i}{\sum_{k=1}^Mf_k} pi=∑k=1Mfkfi
当个体选择的概率给定后,产生[0,1]之间均匀随机数来决定哪个个体参加交配。若个体的选择概率大,则有机会被多次选中,那么它的遗传基因就会在种群中扩大;若个体的选择概率小,则被淘汰的可能性会大。
def selection(chroms):
probs = fitness/np.sum(fitness)
probs_cum = np.cumsum(probs)
each_rand = np.random.uniform(size=len(fitness))
selected_chroms = np.array([chroms[np.where(probs_cum > rand)[0][0]] for rand in each_rand])
return selected_chroms
selected_chroms = selection(chroms, fitness)
print(f(decode(selected_chroms)))
>>>
[2.04387992 2.00281338 2.04387992 2.0806576 2.00281338 2.04860442
2.00281338 2.04387992 2.09053176 2.0806576 ]
交叉
交叉操作是指从种群中随机选择两个个体,通过两个染色体的交换组合,把父串的优秀特征遗传给子串,从而产生新的优秀个体。
这里在染色体中间进行交叉。
def crossover(selected_chroms, prob=0.6):
# cross over
pairs = np.random.permutation(int(len(selected_chroms)*prob//2*2)).reshape(-1, 2)
center = len(selected_chroms[0])//2
for i, j in pairs:
# 在中间位置交叉
x, y = selected_chroms[i], selected_chroms[j]
selected_chroms[i] = x[:center] + y[center:]
selected_chroms[j] = y[:center] + x[center:]
return selected_chroms
cross_chroms = crossover(selected_chroms)
print(f(decode(cross_chroms)))
>>>
[2.03375504 2.00776988 2.04387992 2.09293383 2.00281338 2.02964522
2.00281338 2.04387992 2.09053176 2.0806576 ]
变异
为了防止遗传算法在优化过程中陷入局部最优解,在搜索过程中,需要对个体进行变异,在实际应用中,主要采用单点变异,也叫位变异,即只需要对基因序列中某一个位进行变异,以二进制编码为例,即0变为1,而1变为0。群体 G t G_t Gt经过选择、交叉、变异运算后得到下一代群体 G t + 1 G_{t+1} Gt+1。
def mutate(chroms, prob=0.1):
clen = len(chroms[0])
m = {'0':'1', '1':'0'}
newchroms = []
each_prob = np.random.uniform(size=len(chroms))
for i, chrom in enumerate(chroms):
if each_prob[i] < prob:
pos = np.random.randint(clen)
chrom = chrom[:pos] + m[chrom[pos]] + chrom[pos+1:]
newchroms.append(chrom)
return np.array(newchroms)
muatate_chroms = mutate(cross_chroms)
print(f(decode(muatate_chroms)))
>>>
[2.03375504 2.00776988 2.04555749 2.09293383 2.00281338 2.02964522
2.00281338 2.04387992 2.09053176 2.0806576 ]
主程序
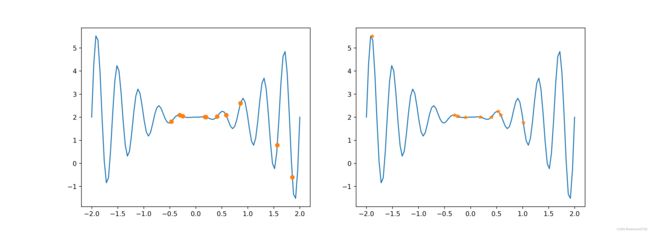
def PltTwoChroms(chroms1, chroms2, fitfun):
Xs = np.linspace(-2, 2, 100)
fig, (axs1, axs2) = plt.subplots(1, 2, figsize=(14, 5))
dechroms = decode(chroms1)
fitness = fitfun(dechroms)
axs1.plot(Xs, fitfun(Xs))
axs1.plot(dechroms, fitness, 'o')
dechroms = decode(chroms2)
fitness = fitfun(dechroms)
axs2.plot(Xs, fitfun(Xs))
axs2.plot(dechroms, fitness, '*')
plt.show()
np.random.seed(0)
population = init_population(10)
chroms = encode(population)
init_chroms = chroms.copy()
best_population = None
best_finess = -np.inf
for i in range(1000):
fitness = f(decode(chroms))
# for fitness to be positive
fitness = fitness - fitness.min() + 0.000001
if np.max(fitness) > np.max(best_finess):
best_finess = fitness
best_population = decode(chroms)
selected_chroms = selection(chroms, fitness)
crossed_chroms = crossover(selected_chroms)
mutated_chroms = mutate(cross_chroms, 0.5)
chroms = mutated_chroms
PltTwoChroms(init_chroms, encode(best_population), f)
关于遗传算法的一些思考
关于遗传算法的应用需要具体问题具体分析。算法的每个步骤(染色体编解码,选择,交叉,变异),以及每个步骤的超参数,都需要根据实际情况来调整, 通过反复的试验找到最优解。
附录
完整代码如下:
import numpy as np
class GeneticTool:
def __init__(self, _min=-2, _max=2, _scale=1e4, _width=10, population_size=10):
self._min = _min
self._max = _max
self._scale = _scale
self._width = _width
self.population_size = population_size
self.init_population = np.random.uniform(low=_min, high=_max, size=population_size)
@staticmethod
def fitness_function(x):
return x**2 * np.sin(5*np.pi*x) + 2
def encode(self, population):
_scaled_population = (population - self._min) * self._scale
chroms = np.array([np.binary_repr(x, width=self._width) for x in _scaled_population.astype(int)])
return chroms
def decode(self, chroms):
res = np.array([(int(x, base=2)/self._scale) for x in chroms])
res += self._min
return res
@staticmethod
def selection(chroms, fitness):
fitness = fitness - np.min(fitness) + 1e-5
probs = fitness/np.sum(fitness)
probs_cum = np.cumsum(probs)
each_rand = np.random.uniform(size=len(fitness))
selected_chroms = np.array([chroms[np.where(probs_cum > rand)[0][0]] for rand in each_rand])
return selected_chroms
@staticmethod
def crossover(chroms, prob):
pairs = np.random.permutation(int(len(chroms)*prob//2*2)).reshape(-1, 2)
center = len(chroms[0])//2
for i, j in pairs:
# cross over in center
x, y = chroms[i], chroms[j]
chroms[i] = x[:center] + y[center:]
chroms[j] = y[:center] + x[center:]
return chroms
@staticmethod
def mutate(chroms, prob):
m = {'0':'1', '1':'0'}
mutate_chroms = []
each_prob = np.random.uniform(size=len(chroms))
for i, chrom in enumerate(chroms):
if each_prob[i] < prob:
# mutate in a random bit
clen = len(chrom)
ind = np.random.randint(clen)
chrom = chrom[:ind] + m[chrom[ind]] + chrom[ind+1:]
mutate_chroms.append(chrom)
return np.array(mutate_chroms)
def run(self, num_epoch):
# select best population
best_population = None
best_finess = -np.inf
population = self.init_population
chroms = self.encode(population)
for i in range(num_epoch):
population = self.decode(chroms)
fitness = self.fitness_function(population)
fitness = fitness - fitness.min() + 1e-4
if np.max(fitness) > np.max(best_finess):
best_finess = fitness
best_population = population
chroms = self.encode(self.init_population)
selected_chroms = self.selection(chroms, fitness)
crossed_chroms = self.crossover(selected_chroms, 0.6)
mutated_chroms = self.mutate(crossed_chroms, 0.5)
chroms = mutated_chroms
# select best individual
return best_population[np.argmax(best_finess)]
if __name__ == '__main__':
np.random.seed(0)
gt = GeneticTool(_min=-2, _max=2, _scale=1e10, _width=10, population_size=10)
res = gt.run(1000)
print(res)