图论(Python networkx)
一、无负权值的单源最短路径模型(Dijkstra)
Dijkstra算法适用于单源、无负权值、有向图或无向图的最短路径模型
1、基本模型
以下图为例,求节点0到其他节点的最短路径
2、代码实现
import networkx as nx
#创建有向图
graph = nx.DiGraph()
#创建下标为0开始的6个节点
graph.add_nodes_from(range(0, 6))
#输入带权边的数据
edges = [(0, 1, 2), (0, 2, 3), (0, 4, 7), (0, 5, 2),
(2, 3, 5), (2, 4, 1),
(4, 3, 3), (4, 5, 2)]
#输入边
graph.add_weighted_edges_from(edges)
#求解
sd = []
sd_path = []
for i in range(0, 6):
sd.append(nx.dijkstra_path_length(graph, 0, i, weight='weight'))
sd_path.append(nx.dijkstra_path(graph, 0, i, weight='weight'))
#输出结果
print("最短路径值为:", sd)
print("最短路径为:", sd_path)3、输出结果
最短路径值为: [0, 2, 3, 7, 4, 2]
最短路径为: [[0], [0, 1], [0, 2], [0, 2, 4, 3], [0, 2, 4], [0, 5]]
二、存在负权值的单源最短路径模型(Bellman-ford)
Bellman-ford算法适用于单源、可有负权值、无负权值环、有向图或无向图的最短路径模型
1、基本模型
以下图为例,求节点0到其他节点的最短路径
2、代码求解
import networkx as nx
#创建有向图
graph = nx.DiGraph()
#创建下标为0开始的6个顶点
graph.add_nodes_from(range(0, 6))
#输入带权边的数据
edges = [(0, 1, 4), (0, 2, 3), (0, 4, 3), (0, 5, 1),
(1, 2, -2),
(2, 3, 5), (2, 4, -2),
(4, 3, 3), (4, 5, 3)]
#输入边
graph.add_weighted_edges_from(edges)
#求解
sd = []
sd_path = []
for i in range(0, 6):
sd.append(nx.bellman_ford_path_length(graph, 0, i, weight='weight'))
sd_path.append(nx.bellman_ford_path(graph, 0, i, weight='weight'))
#输出结果
print("最短路径值为:", sd)
print("最短路径为:", sd_path)3、输出结果
最短路径值为: [0, 4, 2, 3, 0, 1]
最短路径为: [[0], [0, 1], [0, 1, 2], [0, 1, 2, 4, 3], [0, 1, 2, 4], [0, 5]]
三、多源最短路径模型(Floyd)
Floyd算法适用于多源、可有负权值、有向图或无向图的最短路径模型
1、基本模型
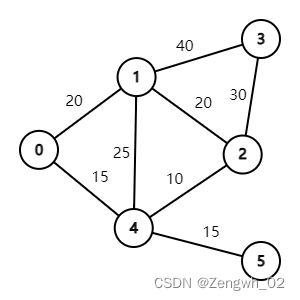
以下图为例,求所有节点之间的最短路径
2、代码求解
import networkx as nx
#创建无向图
graph = nx.Graph()
#创建下标为0开始的6个节点
graph.add_nodes_from(range(0, 6))
#输入带权边的数据
edges = [(0, 1, 20), (0, 4, 15),
(1, 2, 20), (1, 3, 40), (1, 4, 25),
(2, 3, 30), (2, 4, 10),
(4, 5, 15)]
#输入边
graph.add_weighted_edges_from(edges)
#求解
sd = dict(nx.shortest_path_length(graph, weight='weight'))
sd_path = dict(nx.shortest_path(graph, weight='weight'))
#输出结果
for i in range(0, 6):
for j in range(0, 6):
print("{}->{}的最短路径值为{}\t最短路径为:{}".format(i, j, sd[i][j], sd_path[i][j]))3、输出结果
0->0的最短路径值为0 最短路径为:[0]
0->1的最短路径值为20 最短路径为:[0, 1]
0->2的最短路径值为25 最短路径为:[0, 4, 2]
0->3的最短路径值为55 最短路径为:[0, 4, 2, 3]
0->4的最短路径值为15 最短路径为:[0, 4]
0->5的最短路径值为30 最短路径为:[0, 4, 5]
1->0的最短路径值为20 最短路径为:[1, 0]
1->1的最短路径值为0 最短路径为:[1]
1->2的最短路径值为20 最短路径为:[1, 2]
1->3的最短路径值为40 最短路径为:[1, 3]
1->4的最短路径值为25 最短路径为:[1, 4]
1->5的最短路径值为40 最短路径为:[1, 4, 5]
2->0的最短路径值为25 最短路径为:[2, 4, 0]
2->1的最短路径值为20 最短路径为:[2, 1]
2->2的最短路径值为0 最短路径为:[2]
2->3的最短路径值为30 最短路径为:[2, 3]
2->4的最短路径值为10 最短路径为:[2, 4]
2->5的最短路径值为25 最短路径为:[2, 4, 5]
3->0的最短路径值为55 最短路径为:[3, 2, 4, 0]
3->1的最短路径值为40 最短路径为:[3, 1]
3->2的最短路径值为30 最短路径为:[3, 2]
3->3的最短路径值为0 最短路径为:[3]
3->4的最短路径值为40 最短路径为:[3, 2, 4]
3->5的最短路径值为55 最短路径为:[3, 2, 4, 5]
4->0的最短路径值为15 最短路径为:[4, 0]
4->1的最短路径值为25 最短路径为:[4, 1]
4->2的最短路径值为10 最短路径为:[4, 2]
4->3的最短路径值为40 最短路径为:[4, 2, 3]
4->4的最短路径值为0 最短路径为:[4]
4->5的最短路径值为15 最短路径为:[4, 5]
5->0的最短路径值为30 最短路径为:[5, 4, 0]
5->1的最短路径值为40 最短路径为:[5, 4, 1]
5->2的最短路径值为25 最短路径为:[5, 4, 2]
5->3的最短路径值为55 最短路径为:[5, 4, 2, 3]
5->4的最短路径值为15 最短路径为:[5, 4]
5->5的最短路径值为0 最短路径为:[5]
四、稀疏图的最小生成树模型(Kruskal)
Kruskal算法对边进行操作,初始最小生成树边数为0,每迭代一次就将一条满足条件的最小代价边,加入到最小生成树的边集合中。因此,Kruskal算法常用于稀疏图的最小生成树模型。
1、基本模型
以下图为例,求该图的最小生成树
2、代码求解
import networkx as nx
#创建无向图
graph = nx.Graph()
#创建以下标为1开始的5个顶点
graph.add_nodes_from(range(1, 6))
#输入带权边的数据
edges = [(1, 2, 8), (1, 3, 4), (1, 5, 2),
(2, 3, 4),
(3, 4, 2), (3, 5, 1),
(4, 5, 5)]
#输入边
graph.add_weighted_edges_from(edges)
#求解
min_tree = nx.minimum_spanning_tree(graph, weight='weight', algorithm='kruskal')
min_tree_dict = nx.get_edge_attributes(min_tree, 'weight')
tree_size = sum(min_tree_dict.values())
#输出结果
print("最小生成树为:", min_tree_dict)
print("最小生成树大小为:", tree_size)3、输出结果
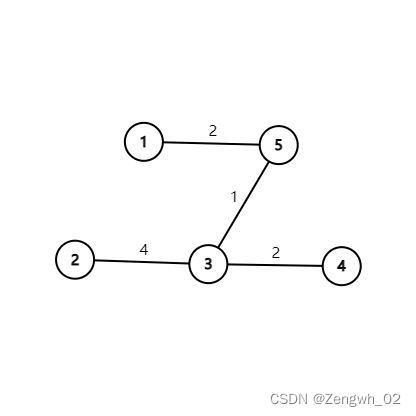
最小生成树为: {(1, 5): 2, (2, 3): 4, (3, 5): 1, (3, 4): 2}
最小生成树大小为: 9
最小生成树如下图所示
五、稠密图的最小生成树模型(Prim)
Prim算法对节点进行操作,初始最小生成树节点为一个任意的开始节点,每迭代一次就将一个满足条件的最小代价节点,加入到最小生成树的节点集合中。因此,Prim算法常用于稠密图的最小生成树模型。
1、基本模型
以下图为例,求该图的最小生成树模型
2、 代码求解
import networkx as nx
import math
#创建无向图
graph = nx.Graph()
#创建以下标为1开始的8个顶点
graph.add_nodes_from(range(1, 9))
#输入带权边的数据
edges = [(1, 2, 1.3), (1, 3, 2.1), (1, 4, 0.9), (1, 5, 0.7), (1, 6, 1.8), (1, 7, 2.0), (1, 8, 1.5),
(2, 3, 0.9), (2, 4, 1.8), (2, 5, 1.2), (2, 6, 2.6), (2, 7, 2.3), (2, 8, 1.1),
(3, 4, 2.6), (3, 5, 1.7), (3, 6, 2.5), (3, 7, 1.9), (3, 8, 1.0),
(4, 5, 0.7), (4, 6, 1.6), (4, 7, 1.5), (4, 8, 0.9),
(5, 6, 0.9), (5, 7, 1.1), (5, 8, 0.8),
(6, 7, 0.6), (6, 8, 1.0),
(7, 8, 0.5)]
#输入边
graph.add_weighted_edges_from(edges)
#求解
min_tree = nx.minimum_spanning_tree(graph, weight='weight', algorithm='prim')
min_tree_dict = nx.get_edge_attributes(min_tree, 'weight')
tree_size = math.fsum(min_tree_dict.values())
#输出结果
print("最小生成树为:", min_tree_dict)
print("最小生成树大小为:", tree_size)3、输出结果
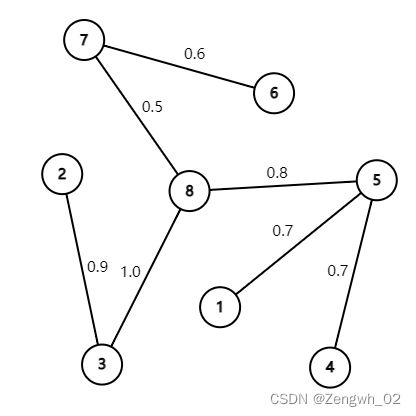
最小生成树为: {(1, 5): 0.7, (2, 3): 0.9, (3, 8): 1.0, (4, 5): 0.7, (5, 8): 0.8, (6, 7): 0.6, (7, 8): 0.5}
最小生成树大小为: 5.2
最小生成树如下图所示