《特征工程入门与实践》--特征选择

《特征工程入门与实践》 -特征选择

元指标

元指标是指不直接与模型预测性能相关的指标，它们试图衡量周遭的性能，包括：

• 模型拟合/训练所需的时间；

• 拟合后的模型预测新实例的时间；

• 需要持久化（永久保存）的数据大小。

为了跟踪这些指标，我们可以创建一个get_best_model_and_accuracy函数以评估若干模型，同时精细到可以提供每个模型的指标。我们会利用函数，完成以下任务：

• 搜索所有给定的参数，优化机器学习流水线；
• 输出有助于评估流水线质量的指标。

# 导入网格搜索模块
from sklearn.model_selection import GridSearchCV

def get_best_model_and_accuracy(model, params, X, y):
    grid = GridSearchCV(model, # 要搜索的模型
                        params, # 要尝试的参数
                        error_score=0.) # 如果报错，结果是0
    grid.fit(X, y) # 拟合模型和参数
    # 经典的性能指标
    print("Best Accuracy: {}".format(grid.best_score_))
    # 得到最佳准确率的最佳参数
    print("Best Parameters: {}".format(grid.best_params_))
    # 拟合的平均时间（秒）
    print("Average Time to Fit (s):  
	{}".format(round(grid.cv_results_['mean_fit_time'].mean(), 3)))
    # 预测的平均时间（秒）
    # 从该指标可以看出模型在真实世界的性能
    print("Average Time to Score (s): 
	{}".format(round(grid.cv_results_['mean_score_time'].mean(), 3)))

我们会用这个函数评估每个特征选择方法，带来一种标准化的感觉。

案例分析：信用卡逾期数据集

import pandas as pd
import numpy as np

# 用随机数种子保证随机数永远一致
np.random.seed(123)

# archive.ics.uci.edu/ml/datasets/default+of+credit+card+clients
# 导入数据集
credit_card_default = pd.read_csv('../data/credit_card_default.csv')

先进行基本的探索性数据分析。检查一下数据集的大小，代码如下：

# 30 000行，24列
credit_card_default.shape

# 描述性统计
# 调用.T方法进行转置，以便更好地观察
credit_card_default.describe().T

default payment next month（下个月逾期）是响应，其他都是特征，特征的尺度迥异，是我们选择数据处理方法和模型时需要考虑的因素。

# 检查缺失值，本数据集中不存在
credit_card_default.isnull().sum()

LIMIT_BAL                     0
SEX                           0
EDUCATION                     0
MARRIAGE                      0
AGE                           0
PAY_0                         0
PAY_2                         0
PAY_3                         0
PAY_4                         0
PAY_5                         0
PAY_6                         0
BILL_AMT1                     0
BILL_AMT2                     0
BILL_AMT3                     0
BILL_AMT4                     0
BILL_AMT5                     0
BILL_AMT6                     0
PAY_AMT1                      0
PAY_AMT2                      0
PAY_AMT3                      0
PAY_AMT4                      0
PAY_AMT5                      0
PAY_AMT6                      0
default payment next month    0
dtype: int64

没有缺失值。接下来设置变量，代码如下：

# 特征矩阵
X = credit_card_default.drop('default payment next month', axis=1)

# 响应变量
y = credit_card_default['default payment next month']

和往常一样创建 $X$ 和 $y$ 变量。$X$ 矩阵有30000行和23列，而 $y$ 是长度为30000的Pandas Series。因为要执行分类任务，所以取一个空准确率，确保机器学习的性能比基准更好。代码如下：

# 取空准确率
y.value_counts(normalize=True)

0    0.7788
1    0.2212

本例需要击败77.88%这个准确率，也就是没有逾期者的比例(0代表没有逾期)。

创建基准机器学习流水线

# 导入4种模型
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier

先建立一些变量，代码如下：

# 为网格搜索设置变量
# 先设置机器学习模型的参数

# 逻辑回归
lr_params = {'C':[1e-1, 1e0, 1e1, 1e2], 'penalty':['l1', 'l2']}

# KNN
knn_params = {'n_neighbors': [1, 3, 5, 7]}

# 决策树
tree_params = {'max_depth':[None, 1, 3, 5, 7]}

# 随机森林
forest_params = {'n_estimators': [10, 50, 100], 'max_depth': [None, 1, 3, 5, 7]}

导入后执行get_best_model_and_accuracy函数，取得每个模型处理原始数据的基准。

因为我们通过函数设置模型，而这会调用一个网格搜索模型，所以只需要创建空白模型即可，代码如下：

# 实例化机器学习模型
lr = LogisticRegression()
knn = KNeighborsClassifier()
d_tree = DecisionTreeClassifier()
forest = RandomForestClassifier()

我们在所有的模型上运行评估函数，了解一下效果的好坏。记住，我们要击败的精确率是0.7788，也就是基线空准确率。运行模型的代码如下：

get_best_model_and_accuracy(lr, lr_params, X, y)

Best Accuracy: 0.809566666667
Best Parameters: {'penalty': 'l1', 'C': 0.1}
Average Time to Fit (s): 0.602
Average Time to Score (s): 0.002

在KNN上做同样的处理：

get_best_model_and_accuracy(knn, knn_params, X, y)

Best Accuracy: 0.760233333333
Best Parameters: {'n_neighbors': 7}
Average Time to Fit (s): 0.035
Average Time to Score (s): 0.88

KNN是按照欧几里得距离进行预测的，在非标准数据上可能会失效，但是其他3个算法不会受此影响.

KNN是基于距离的模型，使用空间的紧密度衡量，假定所有的特征尺度相同，但是我们知道数据并不是这样。因此对于KNN，我们需要更复杂的流水线，以更准确地评估基准性能。代码如下：

# 导入所需的包
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

# 为流水线设置KNN参数
knn_pipe_params = {'classifier__{}'.format(k): v for k, v in knn_params.items()}

# KNN需要标准化的参数
knn_pipe = Pipeline([('scale', StandardScaler()), ('classifier', knn)])


# 拟合快，预测慢
get_best_model_and_accuracy(knn_pipe, knn_pipe_params, X, y)

print(knn_pipe_params)  # {'classifier__n_neighbors': [1, 3, 5, 7]}

Best Accuracy: 0.8008
Best Parameters: {'classifier__n_neighbors': 7}
Average Time to Fit (s): 0.035
Average Time to Score (s): 6.723

在用StandardScalar进行$z$分数标准化处理后，这个流水线的准确率至少比空准确率要高，但是这也严重影响了预测时间，因为多了一个预处理步骤。

从更简单的决策树开始：

get_best_model_and_accuracy(d_tree, tree_params, X, y)

Best Accuracy: 0.820266666667
Best Parameters: {'max_depth': 3}
Average Time to Fit (s): 0.158
Average Time to Score (s): 0.002

决策树的拟合速度比逻辑回归快，预测速度比KNN快。最后测试一下随机森林，代码如下：

get_best_model_and_accuracy(forest, forest_params, X, y)

Best Accuracy: 0.819566666667
Best Parameters: {'n_estimators': 50, 'max_depth': 7}
Average Time to Fit (s): 1.107
Average Time to Score (s): 0.044

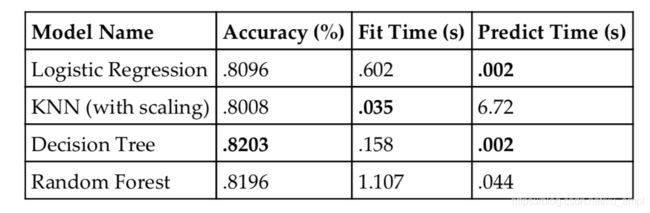
比逻辑回归和KNN好得多，但是没有决策树好。我们汇总一下结果，看看应该使用哪个模型。

决策树的准确率最高，并且预测时间和逻辑回归并列第一，而带缩放的KNN拟合最快。总体而言，决策树应该是最适合下一步采用的模型，因为它在两个最重要的指标上领先：

• 我们想要最高的准确率，以保证预测的准确性；
• 考虑到实时生产环境，预测时间低大有裨益。

特征选择的类型:

选择特征是为了提高预测能力，降低时间成本。所以这里介绍两种类型：基于统计和基于模型的特征选择。基于统计的特征选择很大程度上依赖于机器学习模型之外的统计测试，以便在流水线的训练阶段选择特征。基于模型的特征选择则依赖于一个预处理步骤，需要训练一个辅助的机器学习模型，并利用其预测能力来选择特征。

这两种类型都试图从原始特征中选择一个子集，减少数据大小，只留下预测能力最高的特征。

基于统计的特征选择

通过统计数据，我们可以快速、简便地解释定量和定性数据。本章会使用两个新概念帮我们选择特征：

• 皮尔逊相关系数（Pearson correlations）；
• 假设检验。

这两个方法都是单变量方法。意思是，如果为了提高机器学习流水线性能而每次选择单一特征以创建更好的数据集，这种方法最简便。

皮尔逊相关系数

我们其实已经见过相关系数了，但并非用于特征选择。我们已经知道，可以这样计算相关系数：

credit_card_default.corr()

皮尔逊相关系数（是Pandas默认的）会测量列之间的线性关系。该系数在$-1～1$变化，$0$代表没有线性关系。相关性接近$-1$或$1$代表线性关系很强。

值得注意的是，皮尔逊相关系数要求每列是正态分布的（我们没有这样假设）。在很大程度上，我们也可以忽略这个要求，因为数据集很大（超过500的阈值）$1$。

Pandas的.corr()方法会为所有的列计算皮尔逊相关系数。这个24 × 24的矩阵很难读，我们用热图优化一下：

# 用Seaborn生成热图
import seaborn as sns
import matplotlib.style as style
# 选用一个干净的主题
style.use('fivethirtyeight')
sns.heatmap(credit_card_default.corr())

生成的热图如下图所示。

注意，heatmap函数会自动选择最相关的特征进行展示。不过，我们目前关注特征和响应变量的相关性。我们假设，和响应变量越相关，特征就越有用。不太相关的特征应该没有什么用。

用下面的代码隔离特征和响应变量的相关性：

# 只有特征和响应的相关性
credit_card_default.corr()['default payment next month']

LIMIT_BAL                    -0.153520
SEX                          -0.039961
EDUCATION                     0.028006
MARRIAGE                     -0.024339
AGE                           0.013890
PAY_0                         0.324794
PAY_2                         0.263551
PAY_3                         0.235253
PAY_4                         0.216614
PAY_5                         0.204149
PAY_6                         0.186866
BILL_AMT1                    -0.019644
BILL_AMT2                    -0.014193
BILL_AMT3                    -0.014076
BILL_AMT4                    -0.010156
BILL_AMT5                    -0.006760
BILL_AMT6                    -0.005372
PAY_AMT1                     -0.072929
PAY_AMT2                     -0.058579
PAY_AMT3                     -0.056250
PAY_AMT4                     -0.056827
PAY_AMT5                     -0.055124
PAY_AMT6                     -0.053183
default payment next month    1.000000
Name: default payment next month, dtype: float64

最后一行可以忽略，因为这是响应变量和自己的相关性。我们寻找相关系数接近$-1$或$1$的特征，因为这些特征应该会对预测有用。我们用Pandas过滤出相关系数超过正负$0.2$的特征。
先定义一个Pandas mask作为过滤器：

# 只留下相关系数超过正负0.2的特征

credit_card_default.corr()['default payment next month'].abs() > .2

LIMIT_BAL                     False
SEX                           False
EDUCATION                     False
MARRIAGE                      False
AGE                           False
PAY_0                          True
PAY_2                          True
PAY_3                          True
PAY_4                          True
PAY_5                          True
PAY_6                         False
BILL_AMT1                     False
BILL_AMT2                     False
BILL_AMT3                     False
BILL_AMT4                     False
BILL_AMT5                     False
BILL_AMT6                     False
PAY_AMT1                      False
PAY_AMT2                      False
PAY_AMT3                      False
PAY_AMT4                      False
PAY_AMT5                      False
PAY_AMT6                      False
default payment next month     True
Name: default payment next month, dtype: bool

上面Pandas Series中的False代表特征的相关系数在$-0.2～0.2$，True则代表相关系数超过了正负0.2。我们用下面的代码结合这个mask：

# 存储特征
highly_correlated_features = credit_card_default.columns[credit_card_default.corr()['default payment next month'].abs() > .2]

highly_correlated_features

Index(['PAY_0', 'PAY_2', 'PAY_3', 'PAY_4', 'PAY_5',
       'default payment next month'],
      dtype='object')

highly_correlated_features变量会存储与响应变量高度相关的特征，但是需要删掉响应列的名称，包括这列等于作弊：

# 删掉响应变量
highly_correlated_features = highly_correlated_features.drop('default payment next month')

highly_correlated_features

 Index([u'PAY_0', u'PAY_2', u'PAY_3', u'PAY_4', u'PAY_5'], 
 dtype='object')

留下原始数据集的5个特征，用于预测响应变量。

# 只有5个高度关联的变量
X_subsetted = X[highly_correlated_features]

get_best_model_and_accuracy(d_tree, tree_params, X_subsetted, y)

# 略差一点，但是拟合快了约20倍
Best Accuracy: 0.819666666667
Best Parameters: {'max_depth': 3}
Average Time to Fit (s): 0.01
Average Time to Score (s): 0.002

准确率比要击败的准确率0.8203略差，但是拟合时间快了大概20倍。模型只需要5个特征就可以学习整个数据集，而且速度快得多。

接下来将相关性选择作为预处理阶段的一部分。我们需要创建一个自定义转换器调用刚才的逻辑，并封装为流水线可以使用的类。
将这个类命名为CustomCorrelationChooser，它会实现一个拟合逻辑和一个转换逻辑。

• 拟合逻辑：从特征矩阵中选择相关性高于阈值的列。
• 转换逻辑：对数据集取子集，只包含重要的列。

from sklearn.base import TransformerMixin, BaseEstimator

class CustomCorrelationChooser(TransformerMixin, BaseEstimator):
    def __init__(self, response, cols_to_keep=[], threshold=None):
        # 保存响应变量
        self.response = response
        # 保存阈值
        self.threshold = threshold
        # 初始化一个变量，存放要保留的特征名
        self.cols_to_keep = cols_to_keep

    def transform(self, X):
        # 转换会选择合适的列
        return X[self.cols_to_keep]

    def fit(self, X, *_):
        # 创建新的DataFrame，存放特征和响应
        df = pd.concat([X, self.response], axis=1)
        # 保存高于阈值的列的名称
        self.cols_to_keep = df.columns[df.corr()[df.columns[-1]].abs() > self.threshold]
        # 只保留X的列，删掉响应变量
        self.cols_to_keep = [c for c in self.cols_to_keep if c in X.columns]
        return self

运行下面的新的相关特征选择器：

# 实例化特征选择器
ccc = CustomCorrelationChooser(threshold=.2, response=y)
ccc.fit(X)

ccc.cols_to_keep

['PAY_0', 'PAY_2', 'PAY_3', 'PAY_4', 'PAY_5']

这个类的选择和之前一样。我们在 $X$ 矩阵上应用转换，代码如下：

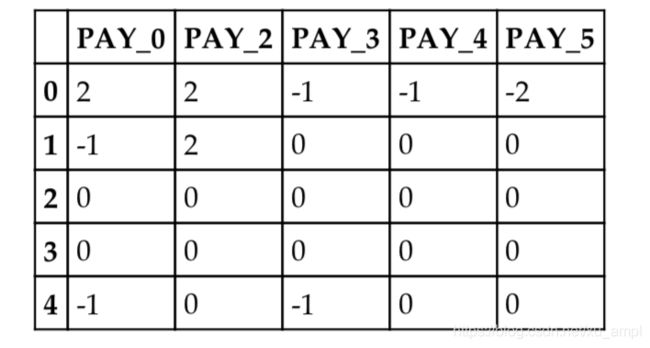
ccc.transform(X).head()

上面代码的输出如下表所示。

我们看见，transform方法删除了其他列，只保留大于0.2阈值的列。现在在流水线中把一切组装起来：

from copy import deepcopy

# 使用响应变量初始化特征选择器
ccc = CustomCorrelationChooser(response=y)

# 创建流水线，包括选择器
ccc_pipe = Pipeline([('correlation_select', ccc),('classifier', d_tree)])

                
tree_pipe_params = {'classifier__max_depth':
      [None, 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]}

# 复制决策树的参数
ccc_pipe_params = deepcopy(tree_pipe_params)

# 更新决策树的参数选择
ccc_pipe_params.update({'correlation_select__threshold':[0, .1, .2, .3]})

print(ccc_pipe_params)  #{'correlation_select__threshold': [0, 0.1, 0.2, 0.3], 'classifier__max_depth': [None, 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]}

# 比原来好一点，而且很快
get_best_model_and_accuracy(ccc_pipe, ccc_pipe_params, X, y)

Best Accuracy: 0.8206
Best Parameters: {'correlation_select__threshold': 0.1, 'classifier__max_depth': 5}
Average Time to Fit (s): 0.105
Average Time to Score (s): 0.003

第一次的特征选择就已经打败了目标。我们的流水线显示，如果把阈值设为0.1，就足以消除噪声以提高准确性，并缩短拟合时间（之前是0.158 s）。
下面看看选择器保留了哪些列：

# 阈值是0.1
ccc = CustomCorrelationChooser(threshold=0.1, response=y)
ccc.fit(X)

# 保留了什么？
ccc.cols_to_keep

['LIMIT_BAL', 'PAY_0', 'PAY_2', 'PAY_3', 'PAY_4', 'PAY_5', 'PAY_6']

选择器保留了我们找到的5列，以及LIMIT_BAL和PAY_6列。这就是scikit-learn中自动化网格搜索的好处，让模型达到最优。

假设检验

假设检验是一种统计学方法，可以对单个特征进行复杂的统计检验。

在特征选择中，假设测试的原则是：“特征与响应变量没有关系”（零假设）为真还是假。我们需要在每个特征上进行检验，并决定其与响应变量是否有显著关系。在某种程度上说，我们的相关性检测逻辑也是这样运作的。我们的意思是，如果某个特征与响应变量的相关性太弱，那么认为“特征与响应变量没有关系”这个假设为真。如果相关系数足够强，那么拒绝该假设，认为特征与响应变量有关。

在将其用于数据之前，需要定义新模块SelectKBest和f_classif，代码如下：

# SelectKBest在给定目标函数后选择k个最高分
from sklearn.feature_selection import SelectKBest

# ANOVA测试
from sklearn.feature_selection import f_classif

# f_classif可以使用负数，但不是所有类都支持
# chi2（卡方）也很常用，但只支持正数
# 回归分析有自己的假设检验

SelectKBest基本上就是包装了一定数量的特征，而这些特征是根据某个标准保留的前几名。在这里，我们使用假设检验的 $p$ 值作为排名依据。

理解 $p$ 值

$p$ 值是介于0和1的小数，代表在假设检验下，给定数据偶然出现的概率。简而言之，$p$ 值越低，拒绝零假设的概率越大。在我们的例子中，$p$ 值越低，这个特征与响应变量有关联的概率就越大，我们应该保留这个特征。

需要注意的是，f_classif 函数在每个特征上单独（单变量测试由此得名）执行一次ANOVA测试（一种假设检验类型），并分配一个 $p$ 值。SelectKBest会将特征按 $p$ 值排列（越小越好），只保留我们指定的 $k$ 个最佳特征。

下面我们用Python试验一下。
首先实例化一个SelectKBest模块。我们手动设定 $k$ 是5，代表只希望保留5个最佳的特征：

# 只保留最佳的5个特征
k_best = SelectKBest(f_classif, k=5)

然后可以像之前使用自定义选择器那样，拟合并转化 $X$ 矩阵，选择需要的特征：

# 选择最佳特征后的矩阵
k_best.fit_transform(X, y)

# 30 000列 × 5行
array([[ 2,  2, -1, -1, -2],
       [-1,  2,  0,  0,  0],
       [ 0,  0,  0,  0,  0],
       ...,
       [ 4,  3,  2, -1,  0],
       [ 1, -1,  0,  0,  0],
       [ 0,  0,  0,  0,  0]])

如果想直接查看 $p$ 值并检查选择了哪些特征，可以深入观察 k_best 变量：

# 取列的p值
k_best.pvalues_

# 特征和p值组成DataFrame
# 按p值排列
p_values = pd.DataFrame({'column': X.columns, 'p_value': k_best.pvalues_}).sort_values('p_value')

# 前5个特征
p_values.head()

可以看到，我们的选择器认为PAY_X是最重要的特征。观察 $p$ 值，我们可以看见，这些特征的$p$值极小，几乎为0。$p$ 值的一个常见阈值是0.05，意思是可以认为$p$值小于0.05的特征是显著的。对于我们的测试，这些列是极其重要的。
用下面的代码看看哪些列的 p_value 较高：

# 高p值的特征
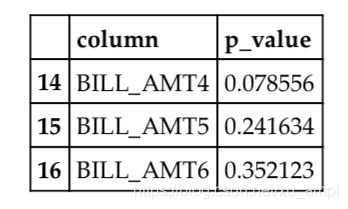
p_values[p_values['p_value'] >= .05]

结果如下表所示。

有3个特征的 $p$ 值较高。我们可以在流水线中应用SelectKBest，看看是否效果更好：

k_best = SelectKBest(f_classif)

# 用SelectKBest建立流水线
select_k_pipe = Pipeline([('k_best', k_best),
 ('classifier', d_tree)])

select_k_best_pipe_params = deepcopy(tree_pipe_params)
# all没有作用
select_k_best_pipe_params.update({'k_best__k':list(range(1,23)) +
['all']})

print(select_k_best_pipe_params) # {'k_best__k': [1, 2, 3, 4, 5, 6,
7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 'all'],
'classifier__max_depth': [None, 1, 3, 5, 7, 9, 11, 13, 15, 17, 19,
21]}

# 与相关特征选择器比较
get_best_model_and_accuracy(select_k_pipe, select_k_best_pipe_params, X, y)

Best Accuracy: 0.8206
Best Parameters: {'k_best__k': 7, 'classifier__max_depth': 5}
Average Time to Fit (s): 0.102
Average Time to Score (s): 0.002

SelectKBest模块和自定义转换器的准确率差不多，但是快了一点。用下面的代码查看选择了哪些特征：

k_best = SelectKBest(f_classif, k=7)

# 最低的7个p值和之前选择的一样
# ['LIMIT_BAL', 'PAY_0', 'PAY_2', 'PAY_3', 'PAY_4', 'PAY_5', 'PAY_6']

p_values.head(7)

代码的结果如下表所示

看起来和之前统计方法的选择相同。我们的统计方法有可能只是按顺序选了这7个特征。

在ANOVA之外，还有其他的测试能用于回归任务，例如卡方检验等。

基于模型的特征选择

本节使用统计方法和测试从原始数据集中选择特征，以优化机器学习流水线的预测性能和时间复杂度。

scikit-learn中CountVectorizer模块可以从文本中构建特征，并用于机器学习流水线。
CountVectorizer有很多参数，在搜索最佳流水线时可以调整。具体来说，有以下几个内置的特征选择参数。

max_features：整数，设置特征构建器可以记忆的最多特征数量。要记忆的特征是由一个排名系统决定的，它依照词项在语料库中的出现次数进行排序。

min_df：浮点数，为词项在语料库中出现的频率设定下限；如果低于该值，则不进行标记。

max_df：浮点数，和min_df类似，设定词项的频率上限。

stop_words：按照内置静态列表对词项类型进行限制。如果词项在stop_words中，那么即使频率在min_df和max_df允许的范围内，也会被省略。

首先引入推文数据集：

# 推文数据集
tweets = pd.read_csv('./twitter_sentiment.csv', encoding='latin1')

我们先创建一个特征和一个响应变量。因为我们处理的是文本，所以特征变量是文本列，而不是二维矩阵：

tweets_X, tweets_y = tweets['SentimentText'], tweets['Sentiment']

可以建立流水线，并用前面使用过的函数get_best_model_and_accuracy进行评估，代码如下：

from sklearn.feature_extraction.text import CountVectorizer
# 导入朴素贝叶斯，加快处理
from sklearn.naive_bayes import MultinomialNB
　
featurizer = CountVectorizer()
　
text_pipe = Pipeline([('featurizer', featurizer),
                      ('classify', MultinomialNB())])
　
text_pipe_params = {'featurizer__ngram_range':[(1, 2)],
                    'featurizer__max_features': [5000, 10000],
                    'featurizer__min_df': [0., .1, .2, .3],
                    'featurizer__max_df': [.7, .8, .9, 1.]}
　
　
get_best_model_and_accuracy(text_pipe, text_pipe_params,
                            tweets_X, tweets_y)
　
Best Accuracy: 0.755753132845
Best Parameters: {'featurizer__min_df': 0.0, 
'featurizer__ngram_range': (1, 2), 'featurizer__max_df': 0.7, 
'featurizer__max_features': 10000}
Average Time to Fit (s): 5.808
Average Time to Score (s): 0.957

数据不错（空准确率是0.564），但是上一章使用FeatureUnion模块来组合TfidfVectorizer和CountVectorizer，比这次的分数还高。
我们测试一下新技术，用SelectKBest和CountVectorizer组合一个流水线。看看这次能否不依赖内置的CountVectorizer选择特征，而是用统计测试：

# 更基础，但是用了SelectKBest的流水线
featurizer = CountVectorizer(ngram_range=(1, 2))
　
select_k_text_pipe = Pipeline([('featurizer', featurizer),
                               ('select_k', SelectKBest()),
                               ('classify', MultinomialNB())])
　
select_k_text_pipe_params = {'select_k__k': [1000, 5000]}
　
　
get_best_model_and_accuracy(select_k_text_pipe,
                            select_k_text_pipe_params,
                            tweets_X, tweets_y)
　
Best Accuracy: 0.755703127344
Best Parameters: {'select_k__k': 10000}
Average Time to Fit (s): 6.927
Average Time to Score (s): 1.448

看起来SelectKBest对于文本数据效果不好。如果没有FeatureUnion，我们不能达到上一章的准确率。无论使用何种方式，拟合和预测的时间都很长：这是因为统计单变量方法在大量特征（例如从文本向量化中获取的特征）上表现不佳。

使用机器学习选择特征

在文本处理中，CountVectorizer内置的特征选择工具表现不错，但是一般处理的是已经有行列结构的数据。我们已经看到了基于纯统计方法的特征选择非常强大，现在研究如何使用这些方法让机器学习变得更好。本节主要使用的两类模型是基于树的模型和线性模型。这两类模型都有特征排列的功能，在对特征划分子集时很有用。

在进一步研究前，我们需要强调，虽然这些方法的逻辑并不相同，但是目标一致：找到最佳的特征子集，优化机器学习流水线。 我们要介绍的第一个方法会涉及拟合训练数据时算法（例如训练决策树和随机森林）内部指标的重要性。

针对基于树的模型

在拟合决策树时，决策树会从根节点开始，在每个节点处贪婪地选择最优分割，优化节点纯净度指标。默认情况下，scikit-learn每步都会优化基尼指数（gini metric）。每次分割时，模型会记录每个分割对整体优化目标的帮助。因此，在树形结构中，这些指标对特征重要性有作用。
为了进一步说明，我们拟合一个决策树，并输出特征重要性，如下所示：

# 创建新的决策树分类器
tree = DecisionTreeClassifier()

tree.fit(X, y)

拟合后，可以用 feature_importances_ 属性展示特征对于拟合树的重要性：

# 注意：还有其他特征

importances = pd.DataFrame({'importance': tree.feature_importances_,
'feature':X.columns}).sort_values('importance', ascending=False)

importances.head()

上表显示，拟合中最重要的特征是PAY_0，和上一章统计模型的结果相匹配。更值得注意的是第2、第3和第5个特征，这3个特征在进行统计测试前没有显示出重要性。这意味着，这种特征选择方法有可能带来一些新的结果。

之前我们使用scikit-learn内置的包装器SelectKBest，基于排序函数（例如ANOVA的 $p$ 值）取前 $k$ 个特征。下面会引入一个新的包装器SelectFromModel，和SelectKBest一样选取最重要的前 $k$ 个特征。但是，它会使用机器学习模型的内部指标来评估特征的重要性，不使用统计测试的 $p$ 值。 我们用下面的代码定义SelectFromModel：

# 和SelectKBest相似，但不是统计测试
from sklearn.feature_selection import SelectFromModel

SelectFromModel和SelectKBest相比最大的不同之处在于不使用 $k$（需要保留的特征数）：SelectFromModel使用阈值，代表重要性的最低限度。通过这种方式，这种基于模型的选择器可以脱离人工筛选的过程，只保留与流水线所需同等数量的特征。我们实例化这个类：

#实例化一个类，按照决策树分类器的内部指标排序重要性，选择特征
select_from_model = SelectFromModel(DecisionTreeClassifier(),threshold=.05)

然后在SelectFromModel上拟合数据，调用transform方法，观察数据选择后的子集：

selected_X = select_from_model.fit_transform(X, y)

selected_X.shape

(30000, 9)

了解了模块的基本原理后，我们可以在流水线中应用选择功能。我们需要击败的准确率是0.8206，之前的相关性选择器和ANOVA都得到了这个准确率（因为选择的特征相同）：

# 为后面加速
tree_pipe_params = {'classifier__max_depth': [1, 3, 5, 7]}
　
from sklearn.pipeline import Pipeline

# 创建基于DecisionTreeClassifier的SelectFromModel
select = SelectFromModel(DecisionTreeClassifier())
　
select_from_pipe = Pipeline([('select', select), ('classifier', d_tree)])
                            　
select_from_pipe_params = deepcopy(tree_pipe_params)
　
select_from_pipe_params.update({
 'select__threshold': [.01, .05, .1, .2, .25, .3, .4, .5, .6, 
 "mean", "median","2.*mean"],
 'select__estimator__max_depth': [None, 1, 3, 5, 7]
 })
　
print(select_from_pipe_params)  
# {'select__threshold': [0.01, 0.05, 0.1, 'mean', 'median', '2.*mean'], 'select__estimator__max_depth': 
[None, 1, 3, 5, 7], 'classifier__max_depth': [1, 3, 5, 7]}
　
get_best_model_and_accuracy(select_from_pipe,select_from_pipe_params, X, y)
　
# 没有比原来的更好
Best Accuracy: 0.820266666667
Best Parameters: {'select__threshold': 0.01, 'select__estimator__max_depth': None, 'classifier__max_depth': 3}
Average Time to Fit (s): 0.192
Average Time to Score (s): 0.002

首先注意，我们可以用一些保留字作为阈值参数的一部分，并不是必须选择表示最低重要性的浮点数。例如，mean的阈值只选择比均值更重要的特征，median的阈值只选择比中位数更重要的特征。我们还可以用这些保留字的倍数，例如2.*mean代表比均值重要两倍的特征。

现在查看基于决策树的选择器选出了哪些特征，可以使用SelectFromModel的get_support()方法。这个方法会返回一个数组，其中的每个布尔值代表一个特征，从而告诉我们保留了哪些特征，如下所示：

# 设置流水线最佳参数
select_from_pipe.set_params(**{'select__threshold': 0.01,
 'select__estimator__max_depth': None,
 'classifier__max_depth': 3})
　
# 拟合数据
select_from_pipe.steps[0][1].fit(X, y)
　
# 列出选择的列
X.columns[select_from_pipe.steps[0][1].get_support()]
　
[u'LIMIT_BAL', u'SEX', u'EDUCATION', u'MARRIAGE', u'AGE', u'PAY_0', 
u'PAY_2', u'PAY_3', u'PAY_6', u'BILL_AMT1', u'BILL_AMT2', 
u'BILL_AMT3', u'BILL_AMT4', u'BILL_AMT5', u'BILL_AMT6', u'PAY_AMT1',
u'PAY_AMT2', u'PAY_AMT3', u'PAY_AMT4', u'PAY_AMT5', u'PAY_AMT6']

这棵树选择了除了两个特征外的所有其他特征，但是和什么都不选的树性能没什么区别。

我们可以继续尝试几种基于树的模型，例如RandomForest（随机森林）和ExtraTreesClassifier（极限随机树）等，但是效果应该比不基于树的方法差。

线性模型和正则化

SelectFromModel可以处理任何包括feature_importances_或coef_属性的机器学习模型。基于树的模型会暴露前者，线性模型则会暴露后者。在拟合后，线性回归、逻辑回归、支持向量机（SVM，support vector machine）等线性模型会将一个系数放在特征的斜率（重要性）前面。SelectFromModel会认为这个系数等同于重要性，并根据拟合时的系数选择特征。
然而，在使用模型之前，我们需要引入正则化的概念，以选择真正有用的特征。

正则化简介

L1正则化也称为lasso正则化，会使用L1范数（参见上面的公式）将向量条目绝对值的和加以限制，使系数可以完全消失。如果系数降为0，那么这个特征在预测时就没有任何意义，而且肯定不会被SelectFromModel选择。

L2正则化也称为岭正则化，施加惩罚L2范数（向量条目的平方和），让系数不会变成0，但是会非常小。

正则化也有助于解决多重共线性的问题，也就是说，数据中有多个线性相关的特征。L1惩罚可以强制其他线性相关特征的系数为0，保证选择器不会选择这些线性相关的特征，有助于解决过拟合问题。

另一个特征重要性指标：线性模型参数和之前用树的方法一样，我们可以用L1和L2正则化为特征选择寻找最佳系数。我们用逻辑回归模型作为选择器，在L1和L2范数上进行网格搜索：

# 用正则化后的逻辑回归进行选择
logistic_selector = SelectFromModel(LogisticRegression())
　
# 新流水线，用LogistisRegression的参数进行排列
regularization_pipe = Pipeline([('select', logistic_selector), ('classifier', tree)])
　
regularization_pipe_params = deepcopy(tree_pipe_params)
　
# L1和L2正则化
regularization_pipe_params.update({
 'select__threshold': [.01, .05, .1, "mean", "median", "2.*mean"],
 'select__estimator__penalty': ['l1', 'l2'],
 })
　
print(regularization_pipe_params)  # {'select__threshold': [0.01, 
0.05, 0.1, 'mean', 'median', '2.*mean'], 'classifier__max_depth': 
[1, 3, 5, 7], 'select__estimator__penalty': ['l1', 'l2']}
　
　
get_best_model_and_accuracy(regularization_pipe,
 regularization_pipe_params,
 X, y)
　
# 比原来的好，实际上是目前最好的，也快得多
Best Accuracy: 0.821166666667
Best Parameters: {'select__threshold': 0.01, 'classifier__max_depth': 5, 'select__estimator__penalty': 'l1'}
Average Time to Fit (s): 0.51
Average Time to Score (s): 0.001

现在的准确率终于超过统计测试选择器了。再次使用SelectFromModel的get_support()方法，列出选择的特征：

# 设置流水线最佳参数
regularization_pipe.set_params(**{'select__threshold': 0.01,'classifier__max_depth': 5,'select__estimator__penalty': 'l1'})
　
# 拟合数据
regularization_pipe.steps[0][1].fit(X, y)
　
# 列出选择的列
X.columns[regularization_pipe.steps[0][1].get_support()]
　
Index(['SEX', 'EDUCATION', 'MARRIAGE', 'PAY_0', 'PAY_2', 'PAY_3', 
'PAY_4','PAY_5'],dtype='object')

基于逻辑回归的选择器选择了大部分的PAY_X特征，也发现了性别、教育和婚姻状况可以帮助预测。

接下来用SelectFromModel模块在支持向量机分类器上进行测试。

支持向量机是分类模型，在空间中绘制线性边界，对二分数据进行分类。这些线性边界叫作支持向量。目前看来，逻辑回归分类器和支持向量分类器（SVC）的最大区别在于，后者会最大优化二分类项目的准确性，而前者对属性的建模更好。像之前决策树和逻辑回归一样，我们用scikit-learn实现一个线性SVC模型，代码如下：

# SVC是线性模型，用线性支持在欧几里得空间内分割数据
# 只能分割二分数据
from sklearn.svm import LinearSVC
　
# 用SVC取参数
svc_selector = SelectFromModel(LinearSVC())
　
svc_pipe = Pipeline([('select', svc_selector),
 ('classifier', tree)])
　
svc_pipe_params =
deepcopy(tree_pipe_params)
　
svc_pipe_params.update({
 'select__threshold': [.01, .05, .1, "mean", "median", "2.*mean"],
 'select__estimator__penalty': ['l1', 'l2'],
 'select__estimator__loss': ['squared_hinge', 'hinge'],
 'select__estimator__dual': [True, False]
 })
　
print(svc_pipe_params)  # 'select__estimator__loss': ['squared_hinge', 'hinge'],'select__threshold': [0.01, 0.05, 0.1, 'mean', 'median', '2.*mean'], 
'select__estimator__penalty': ['l1', 'l2'], 
'classifier__max_depth': [1, 3, 5, 7],  'select__estimator__dual': [True, False]}
　
get_best_model_and_accuracy(svc_pipe,svc_pipe_params, X, y)
　
# 刷新了纪录
Best Accuracy: 0.821233333333
Best Parameters: {'select__estimator__loss':'squared_hinge','select__threshold': 0.01,'select__estimator__penalty': 'l1', 'classifier__max_depth': 5,'select__estimator__dual': False}
Average Time to Fit (s): 0.989
Average Time to Score (s): 0.001

SVC达到了最高的准确率。可以看见拟合时间受到了影响，但是如果能把最快的预测和最好的准确率结合，那么机器学习流水线就会很出色了：基于SVC，利用正则化为决策树分类器找到最佳特征。

下面看看选择器选择了哪些特征来达到目前的最佳准确率：

# 设置流水线最佳参数
svc_pipe.set_params(**{'select__estimator__loss': 'squared_hinge',
 'select__threshold': 0.01,
 'select__estimator__penalty': 'l1',
 'classifier__max_depth': 5,
 'select__estimator__dual': False})
　
# 拟合数据
svc_pipe.steps[0][1].fit(X, y)
　
# 列出选择的列
X.columns[svc_pipe.steps[0][1].get_support()]
　
[u'SEX', u'EDUCATION', u'MARRIAGE', u'PAY_0', u'PAY_2', u'PAY_3', u'PAY_5']

与逻辑回归比，唯一的区别是PAY_4特征。但是可以看到，移除单个特征不会影响流水线的性能。

最后一个很自然的问题是：应该如何选用特征选择方法？理论上说，最理想的状况是，你可以像本章这样多次尝试，但我们知道这样是不可行的。下面是一些经验，可以在判断特征选择方法的优劣时参考。

• 如果特征是分类的，那么从SelectKBest开始，用卡方或基于树的选择器。
• 如果特征基本是定量的（例如本例），用线性模型和基于相关性的选择器一般效果更好。
• 如果是二元分类问题，考虑使用SelectFromModel和SVC，因为SVC会查找优化二元分类任务的系数。

在手动选择前，探索性数据分析会很有益处。不能低估领域知识的重要性。