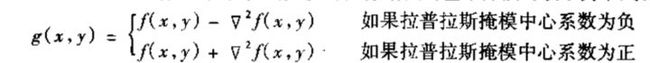【图像处理】边缘检测算子有哪些以及它们之间的对比
这个问题应该是做过传统图像处理的人都接触过的吧。粗略总结下,应该也不会问太细,面试官大概就考察下大家的知识面吧。
综述
边缘检测是图像处理和计算机视觉中,尤其是特征提取中的一个研究领域。图像边缘检测大幅度地减少了数据量,并且剔除了可以认为不相关的信息,保留了图像重要的结构属性。
图像边缘是图像最基本的特征,所谓边缘(Edge) 是指图像局部特性的不连续性。灰度或结构等信息的突变处称之为边缘。例如,灰度级的突变、颜色的突变,、纹理结构的突变等。边缘是一个区域的结束,也是另一个区域的开始,利用该特征可以分割图像。
有许多方法用于边缘检测,它们的绝大部分可以划分为两类:基于查找一类和基于零穿越的一类。
基于查找的方法通过寻找图像一阶导数中的最大和最小值来检测边界,通常是将边界定位在梯度最大的方向。
基于零穿越的方法通过寻找图像二阶导数零穿越来寻找边界,通常是Laplacian过零点或者非线性差分表示的过零点。
当然还有第三种例如被大规模使用的 canny 算子,这个会更加复杂些。
在检测物体边缘时,先对其轮廓点进行粗略检测,然后通过链接规则把原来检测到的轮廓点连接起来,同时也检测和连接遗漏的边界点及去除虚假的边界点。
图像梯度
图像梯度是边缘检测的基础知识,因此在讲边缘算子之前先复习下图像梯度的知识。
一幅图像 f f f 在位置 ( x , y ) (x,y) (x,y) 处的梯度定义如下:
因为图像是一种离散分布,因此求导其实就是做差分, g x g_x gx 和 g y g_y gy 定义如下:
g x = ∂ f ( x , y ) ∂ x = f ( x + 1 , y ) − f ( x , y ) g y = ∂ f ( x , y ) ∂ y = f ( x , y + 1 ) − f ( x , y ) g_x = \frac{\partial f(x,y)}{\partial x} = f(x+1,y) - f(x,y) \\ g_y = \frac{\partial f(x,y)}{\partial y} = f(x,y+1) - f(x,y) gx=∂x∂f(x,y)=f(x+1,y)−f(x,y)gy=∂y∂f(x,y)=f(x,y+1)−f(x,y)
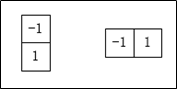
其实上面的这两个公式可以使用下图的一维模板对图像 f ( x , y ) f(x,y) f(x,y) 进行滤波得到。
梯度 ∇ f \nabla f ∇f 表示的是图像 f f f 在位置 ( x , y ) (x,y) (x,y) 处的梯度向量。梯度的方向以及梯度的大小表示如下:
梯度方向:
Θ = a r g t a n ( g y g x ) \Theta=argtan(\frac{g_y}{g_x}) Θ=argtan(gxgy)
梯度大小:
一阶导数的边缘算子
Roberts 算子
Roberts算子是一种利用局部交叉差分寻找边缘的算子,常用来处理具有陡峭的低噪声图像,当图像边缘接近于正45度或负45度时,该算法处理效果更理想。
**优点:**从图像处理的实际效果来看,边缘定位较准,对噪声敏感。适用于边缘明显且噪声较少的图像分割。
**缺点:**提取的边缘线条较粗。
Roberts算子的模板分为水平方向和垂直方向,如下式所示,从其模板可以看出,Roberts算子能较好的增强正负45度的图像边缘。
例如,下面给出Roberts算子的模板,在像素点 P5 处 x x x 和 y y y 方向上的梯度大小 g x g_x gx 和 g y g_y gy 分别计算如下:
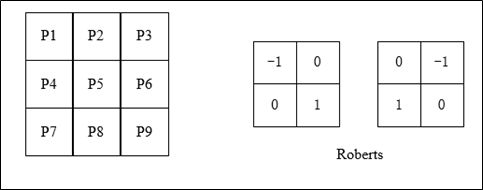
g x = ∂ f ∂ x = P 9 − P 5 g y = ∂ f ∂ y = P 8 − P 6 g_x = \frac{\partial f}{\partial x}=P9-P5 \\ g_y = \frac{\partial f}{\partial y} =P8-P6 gx=∂x∂f=P9−P5gy=∂y∂f=P8−P6
在代码实现方面,便可以如同卷积一样构造两个滤波器矩阵对图像进行卷积,假设使用第一个模板卷积后得到的结果为 f y f_y fy ,使用第二个模板卷积后得到的结果为 f x f_x fx ,那么最终的结果为这两个中间结果的加权平均,例如 0.5 ∗ f x + 0.5 ∗ f y 0.5*f_x +0.5*f_y 0.5∗fx+0.5∗fy 。下同!
Prewitt 算子
Prewitt算子采用 3x3 模板对区域内的像素值进行计算,而Robert算子的模板为 2x2 ,故Prewitt算子的边缘检测结果在水平方向和垂直方向均比Robert算子更加明显。Prewitt算子适合用来识别噪声较多、灰度渐变的图像。
**优点:**Prewitt算子对噪声有抑制作用,抑制噪声的原理是通过像素平均。
**缺点:**该算子具有平滑的作用,但是像素平均相当于对图像的低通滤波,所以Prewitt算子对边缘的定位不如Roberts算子。
同样,下面给出 Prewitt 算子的模板,在像素点 P5 处 x x x 和 y y y 方向上的梯度大小 g x g_x gx 和 g y g_y gy 分别计算如下:

g x = ∂ f ∂ x = ( P 7 + P 8 + P 9 ) − ( P 1 + P 2 + P 3 ) g y = ∂ f ∂ y = ( P 3 + P 6 + P 9 ) − ( P 1 + P 4 + P 7 ) g_x = \frac{\partial f}{\partial x}=(P7+P8+P9)-(P1+P2+P3) \\ g_y = \frac{\partial f}{\partial y}=(P3+P6+P9)-(P1+P4+P7) gx=∂x∂f=(P7+P8+P9)−(P1+P2+P3)gy=∂y∂f=(P3+P6+P9)−(P1+P4+P7)
Sobel 算子
Sobel算子在Prewitt算子的基础上增加了权重的概念,认为相邻点的距离远近对当前像素点的影响是不同的,距离越近的像素点对应当前像素的影响越大,从而实现图像锐化并突出边缘轮廓。因为Sobel算子结合了高斯平滑和微分求导(分化),因此结果会具有更多的抗噪性,当对精度要求不是很高时,Sobel算子是一种较为常用的边缘检测方法。
优点:由于该算子中引入了类似局部平均的运算,因此对噪声具有平滑作用,能很好的消除噪声的影响,边缘定位效果不错。Sobel算子对于象素的位置的影响做了加权,与Prewitt算子、Roberts算子相比因此效果更好。
**缺点:**但检测出的边缘容易出现多像素宽度。
同样,下面给出 Sobel 算子的模板,在像素点 P5 处 x x x 和 y y y 方向上的梯度大小 g x g_x gx 和 g y g_y gy 分别计算如下:
![]()
g x = ∂ f ∂ x = ( P 7 + 2 ∗ P 8 + P 9 ) − ( P 1 + 2 ∗ P 2 + P 3 ) g y = ∂ f ∂ y = ( P 3 + 2 ∗ P 6 + P 9 ) − ( P 1 + 2 ∗ P 4 + P 7 ) g_x = \frac{\partial f}{\partial x}=(P7+2*P8+P9)-(P1+2*P2+P3) \\ g_y = \frac{\partial f}{\partial y}=(P3+2*P6+P9)-(P1+2*P4+P7) gx=∂x∂f=(P7+2∗P8+P9)−(P1+2∗P2+P3)gy=∂y∂f=(P3+2∗P6+P9)−(P1+2∗P4+P7)
二阶微分的边缘算子
Laplacian 算子
Laplace算子是一种各向同性算子,不能检测出边的方向。Laplace算子对孤立象素的响应要比对边缘或线的响应要更强烈,因此只适用于无噪声图象。存在噪声情况下,使用Laplacian算子检测边缘之前需要先进行低通滤波。所以,拉普拉斯算子一般不会用于边的检测,而是常用来判断边缘像素位于图像的明区或暗区。
Laplacian 算子的定义:
L a p l a c i a n ( f ) = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 ∂ 2 f ∂ x 2 = f ( x + 1 ) − f ( x ) ∂ x = [ f ( x + 2 ) − f ( x + 1 ) ] − [ f ( x + 1 ) − f ( x ) ] ∂ 2 f ∂ y 2 = f ( y + 1 ) − f ( y ) ∂ y = [ f ( y + 2 ) − f ( y + 1 ) ] − [ f ( y + 1 ) − f ( y ) ] Laplacian(f)=\frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2} \\ \frac{\partial^2f}{\partial x^2} = \frac{f(x+1)-f(x)}{\partial x} = [f(x+2)-f(x+1)]-[f(x+1)-f(x)] \\ \frac{\partial^2f}{\partial y^2} = \frac{f(y+1)-f(y)}{\partial y} = [f(y+2)-f(y+1)]-[f(y+1)-f(y)] Laplacian(f)=∂x2∂2f+∂y2∂2f∂x2∂2f=∂xf(x+1)−f(x)=[f(x+2)−f(x+1)]−[f(x+1)−f(x)]∂y2∂2f=∂yf(y+1)−f(y)=[f(y+2)−f(y+1)]−[f(y+1)−f(y)]
理论上计算公式是上面那样,但是计算出来后重心感觉有点偏移,为了便于计算以及直观形象,很多教程往往会表示成下面这样:(这是我自己的看法,目前没看到有这样的说法)
∂ 2 f ∂ x 2 = f ( x + 1 ) − f ( x ) ∂ x = [ f ( x + 1 ) − f ( x ) ] − [ f ( x ) − f ( x − 1 ) ] ∂ 2 f ∂ y 2 = f ( y + 1 ) − f ( y ) ∂ y = [ f ( y + 1 ) − f ( y ) ] − [ f ( y ) − f ( y − 1 ) ] \frac{\partial^2f}{\partial x^2} = \frac{f(x+1)-f(x)}{\partial x} = [f(x+1)-f(x)]-[f(x)-f(x-1)] \\ \frac{\partial^2f}{\partial y^2} = \frac{f(y+1)-f(y)}{\partial y} = [f(y+1)-f(y)]-[f(y)-f(y-1)] ∂x2∂2f=∂xf(x+1)−f(x)=[f(x+1)−f(x)]−[f(x)−f(x−1)]∂y2∂2f=∂yf(y+1)−f(y)=[f(y+1)−f(y)]−[f(y)−f(y−1)]
两个方向加起来的话:
∇ 2 ( f ) = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 = [ f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) ] − 4 f ( x , y ) \nabla^2(f)=\frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2} =[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)]-4f(x,y) ∇2(f)=∂x2∂2f+∂y2∂2f=[f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)]−4f(x,y)
上述是数学表达形式的拉普拉斯算子,那么我们可以将其表达为模板的形式:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Jkv5iWlJ-1670937566389)(https://raw.githubusercontent.com/xn1997/picgo/master/jqWOwnrSLoE5C3d.jpg)]
从以上的计算过程可以看出,该算子对孤立点或端点更为敏感,因此特别适用于以突出图像中的孤立点、孤立线或线端点为目的的场合。同梯度算子一样,拉普拉斯算子也会增强图像中的噪声,有时用拉普拉斯算子进行边缘检测时,可将图像先进行平滑处理。
由于拉普拉斯是一种微分算子,它的应用可增强图像中灰度突变的区域,减弱灰度的缓慢变化区域。因此,锐化处理可选择拉普拉斯算子对原图像进行处理,产生描述灰度突变的图像,再将拉普拉斯图像与原始图像叠加而产生锐化图像。
拉普拉斯锐化的基本方法可以由下式表示:
我们发现Laplacian算子进行边缘检测并没有像Sobel或Prewitt那样的平滑过程,所以它会对噪声产生较大的响应,并且无法分别得到水平方向、垂直方向或者其他固定方向的的边缘。但是它只有一个卷积核,所以计算成本会更低。
图像的一阶导数可以用于检测图像中的一个点是否在斜坡上;二阶导数的符号可以用于判断一个边缘点是在边缘亮的一边还是暗的一边。观察下面这张图可以得到答案:当一个边缘点的二阶函数的符号为负时,说明它在亮的一边,符号为正时,在暗的一边。(可以直接死记硬背:亮度跟二阶函数的正负号刚好相反)。
一条连接二阶导数正极值和负极值的虚构直线将在边缘中点附近穿过零点,据此可以用于确定粗边线的中心。
图片来源
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8zRbEdoi-1670937566776)(null)]
Canny
这大概是传统图像里被用的最多的边缘检测算子了。Canny提出了一个对于边缘检测算法的评价标准,包括:
- 以低的错误率检测边缘,也即意味着需要尽可能准确的捕获图像中尽可能多的边缘。
- 检测到的边缘应精确定位在真实边缘的中心。
- 图像中给定的边缘应只被标记一次,并且在可能的情况下,图像的噪声不应产生假的边缘。
简单来说就是,检测算法要做到:边缘要全,位置要准,抵抗噪声的能力要强。
该算子求边缘点的具体算法步骤如下:
- 用高斯滤波器平滑图像:边缘检测算子受噪声的影响都很大。那么,我们第一步就是想到要先去除噪声,因为噪声就是灰度变化很大的地方,所以容易被识别为伪边缘。
- 用一阶偏导有限差分计算梯度幅值和方向,例如 Sobel
- 对梯度幅值进行非极大值抑制:sobel算子检测出来的边缘太粗了,我们需要抑制那些梯度不够大的像素点,只保留最大的梯度,从而达到瘦边的目的。通常灰度变化的地方都比较集中,将局部范围内的梯度方向上,灰度变化最大的保留下来,其它的不保留,这样可以剔除掉一大部分的点。将有多个像素宽的边缘变成一个单像素宽的边缘。即“胖边缘”变成“瘦边缘”。
- 用双阈值算法检测和连接边缘:通过非极大值抑制后,仍然有很多的可能边缘点,进一步的设置一个双阈值,即低阈值(low),高阈值(high)。灰度变化大于high的,设置为强边缘像素,低于low的,剔除。在low和high之间的设置为弱边缘。对每一个弱边缘进一步判断,如果其领域内有强边缘像素,保留,如果没有,剔除。
参考资料
几种边缘检测算子的比较Roberts,Sobel,Prewitt,LOG,Canny
数字图像处理(19): 边缘检测算子(Roberts算子、Prewitt算子、Sobel算子 和 Laplacian算子)
图像处理常用边缘检测算子总结
Laplacian算子-Log算子-Dog算子边缘检测原理合集及实现
Canny边缘检测