Matlab数字图像处理学习记录【2】——亮度变换与空间滤波

一.背景知识

空间域技术则是直接对图像的像素进行操作。有表达式：
$g(x,y)=T[f(x,y)]$ 其中f是输入，g是输出。
还有点(x,y)的临近点定义为.是中心位于(x,y)的正方形或长方形。（这就有意思了，边界可能不填充）

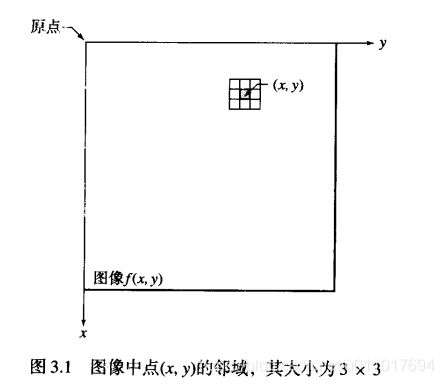
二.亮度变换函数

在灰度图里，亮度就是灰度，而彩色图里，则是每个通道的颜色分量。

2.1函数imadjust

该函数语法:g = imadjust(f, [low_in high_in], [low_out high_out], gamma)

• 简单点来讲，就是将in的值映射到out的值，就可以理解为数学上的那种定义域变化。这俩矩阵的范围都是0~1与图像类型无关，会自适应。
• gamma决定了映射方式是否为线性，可省略，默认值为1。
  
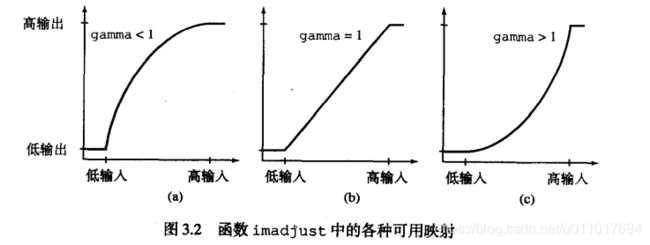
• 若high_out < low_out则亮度还会反转。

2.2对数和对比度拉伸变换

对数缩放是指：如果高频太多，则在图像查看的时候，低频段的东西是不占优势的，高频占了主导，低频就会抑制。所以得想出一种办法对其缩放。后面会介绍这个函数。
而基于此想法，衍生出一种对比度拉伸变换函数。就高频一个高值，低频一个低值，然后中频就由对数级数缩放或者直接阶跃，阶跃情况下，图像则会变成二值图像。
这种方法的函数表达式为：
$s=T(r)=\frac{1}{1+(m/r{)}^E}$ E则是缩放函数的斜率
matlab可以如下表示：
g = 1./(1 + (m./(double(f) + eps)).^E)
简单点，可以直接使用
g = im2uint8(mat2gray (log(1 + double (f))));

2.3整合

我们可以通过自己编写一个函数intrans来实现将前面所学的功能负片、对数、gamma、对比度拉伸变换全部整合：

function g = intrans(f, varargin)
error(nargchk(2, 4, nargin));
classin = class(f);
if strcmp(class(f), 'double') & max(f(:)) > 1 & ~strcmp(varargin{1}, 'log')
    f = mat2gray(f);
else
    f = im2double(f);
end
method = varargin{1};
switch method
    case 'neg'
        g = imcomplement(f);
    case 'log'
        if length(varargin) == 1
            c = 1;
        elseif length(varargin) == 2
            c = varargin{2};
        elseif length(varargin) == 3
            c = varargin{2};
            classin = varargin{3};
        else
            error('Incorrect number of inputs for the log option')
        end
        g = c*(log(1 + double(f)));
    case 'gamma'
        if length(varargin) < 2
            error('Not enough inputs for the gamma option')
        end
        gam = varargin{2};
        g = imadjust(f, [ ], [ ], gam);
    case 'stretch'
        if length(varargin) == 1
            m = mean2(f);
            E = 4.0;
        elseif length(varargin) == 3
            m = varargin{2};
            E = varargin{3};
        else
            error('Incorrect number of inputs for the stretch option')
        end
        g = 1./(1+(m./(f + eps)).^E);
    otherwise
        error('Unknown method')
end
g = changeclass(classin, g);

然后是changeclass这个函数需要自己写：

function image = changeclass(class, varargin)
switch class
case 'uint8'
    image = im2uint8(varargin{:});
case 'uint16'
    image = im2uint16(varargin{:});
case 'double'
    image = im2double(varargin{:});
otherwise
    error('Unsupported IPT data class.');
end

这样我们就可以调用这个整合的函数了：

f = imread('gray.jpg');
g = intrans(f, 'stretch', mean2(im2double(f)), 0.9);
subplot(1,2,1);
imshow(f);
subplot(1,2,2);
imshow(g);

三.直方图处理与绘图函数

按目前来说，直方图在增强，压缩，分割，描述方面扮演着基础性的角色，其他应用后续会介绍，目前是学如何绘制。

3.1生成并绘制直方图

简单来说，就是按照亮度级进行离散化的划分。在[0,G]里有L个亮度级。
具体函数为h = imhist(f, b)
b是要分成多少级，若为空，则默认为G+1
而通过numel(f)可获取f有多少元素，即h = imhist(f, b)/numel(f)即可对直方图归一化。
直接调用imhist(f, b);可以获得直方图，但是这个图很不好看，所以常用其他的绘图方式：
bar(horz, v, width)

• v是我们要绘制的直方图的点组成的行向量
• horz则是一个与v维度相同的向量，用于标记水平标度值，若为空，则默认为length(v)。、
• width默认的是直方图的柱的宽度

axis([horzmin horzmax vertmin vertmax])
则是水平、垂直坐标轴的最小最大值
set(gca, 'xtick\ytick', [])
则可以通过行向量来调整坐标轴的刻度
text(xloc, yloc, 'text str', 'fontsize', 'size')
可以为坐标轴添加文字
title('str')
可以添加标题
有类似的，杆状图：stem(horz, v, 'color_style_marker', 'fill')，fill为是否填充坐标点
还有plot(horz, v, 'color_style_marker')。
其中color_style_marker则是与Python中的参数一致：

最终样式则如下：

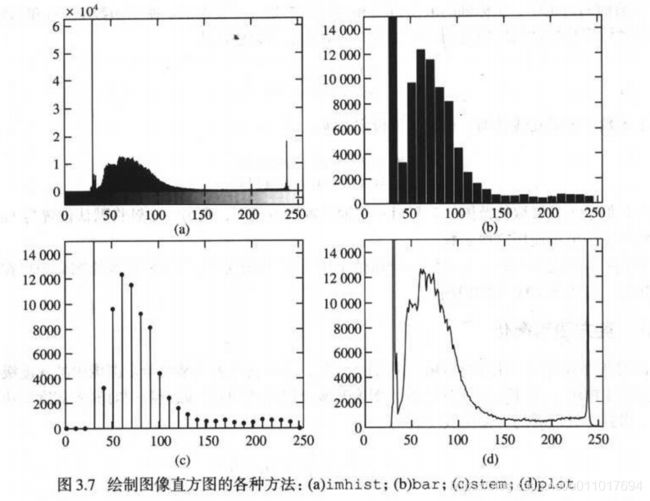
3.2直方图均衡化

假设灰度级归一化至范围[0,1]的连续量，则p_rr表示某给定图像中的灰度级的概率密度函数(PDF)，则对输入灰度级做如下变换，得到输出的灰度级s：
$s=T(r)={\int }_0^r{p}_r(w)dw$ 其中式中w是积分的哑分量，可以看出输出的灰度级的概率密度函数是均匀的:
$$p_s(S)=\{\begin{array}{l}1,0\le s\le 1\\ 0,其他\end{array}$$
反正总的来说，直方图均衡化后，会加局部不够明显的地方，比如画面过亮，则会变暗，过暗则会变，它具有高对比度。
一般来说我们使用函数g = histeq(f, nlev)
其中nlev默认为64.但是为了有最好的效果，需将灰度级设置为最大的可能数量，比如256.
这里可以看看效果:
通过执行代码：

f = imread('gray.jpg');
h = imhist(f);
h1 = h(1:10:256);
axis([0 256 0 15000]);
subplot(2,2,1);
plot(h);
subplot(2,2,3);
imshow(f);
g = histeq(f, 256);
h2 = imhist(g);
subplot(2,2,2);
plot(h2);
subplot(2,2,4);
imshow(g);
figure(2);
hnorm = imhist(f)./numel(f);
cdf = cumsum(hnorm);
x = linspace(0,1,256);
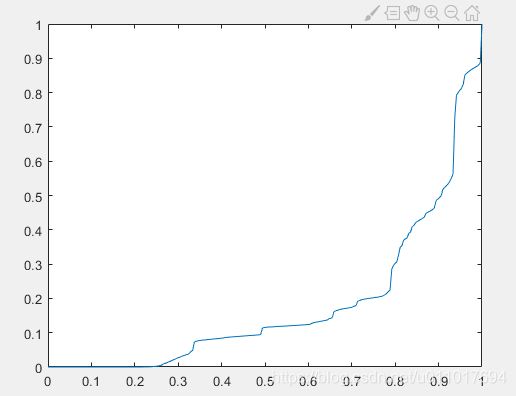
plot(x, cdf);
axis([0 1 0 1]);

由于原图像偏亮，所以我们均衡化后的图像，变得更暗，且可以看到我们cdf的变换函数

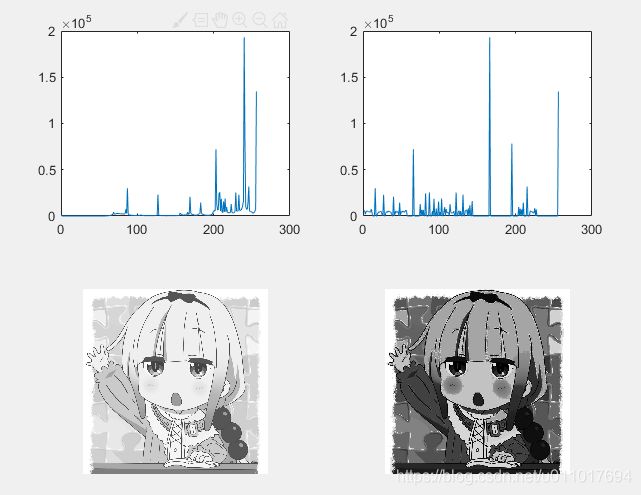
3.2直方图匹配

直方图匹配则就是将图的直方图按给定的直方图进行调整，函数任然用histeq(f, [])后面那个参数不跟数字而是一个行向量。

四.空间滤波

4.1线性空间滤波

说白了就是卷积。先翻转再平移。将卷积核旋转180°后进行对每一个像素平移。
那么可以用该函数：g = imfilter(f, w, mode, boundary, size)

• f是原图像
• w是卷积核
• mode可为：corr或conv。前者是相关对核无操作，后者是卷积会对卷积核旋转180°。
• boundary：边界选项。P边界填充值P、'replicate' 复制边界拓展、symmetric镜像反射其边界拓展、circular将图像看为一个二维周期函数的一个周期进行拓展。
• size：大小选项。'full'则按拓展后，也就是填充后的图像输出，'same'则与输入图像大小一致。

4.2非线性空间滤波

非线性空间滤波是指：类似于线性空间滤波，只不过对每个像素点的操作包含了一个邻域的像素，比如取核内像素的最大值。有俩函数，colfilt和nlfilter一般来说追求速度用colfilt。它会生成一个最大的mn×MN的矩阵A，也就是邻域×图像大小的矩阵。在该矩阵中，每一列对应于中心位于图像内某个位置的邻域所包围的像素。
语法为：g = colfilt(f, [m n], 'sliding', @func, parameters)
@func说的叫函数句柄，也就是C语言中的函数指针。parameters则是func要用到的参数。
函数func则必须对矩阵的每一列操作，返回一个包含所有列的行向量v，v的第k个元素表示的是对A中的第k列进行func操作后的结果。所以A中可以有MN列，v的最大维度为1×MN。
所以我们可以用padarray进行填充：
g = padarray(f, [r c ], method, direction)
r c 是要增加的行列数

比如：

f = [1 2;3 4];
fp = padarray(f, [3 2], 'replicate', 'post');
disp(fp);
%%
     1     2     2     2
     3     4     4     4
     3     4     4     4
     3     4     4     4
     3     4     4     4
%%

五.IPT的标准空间滤波器

5.1线性空间滤波器

生成滤波器的语法w = fspecial('type', parameters)

5.2非线性空间滤波器

ordfilt2可以对图像领域中所包含的像素进行排序，然后使用排序结果确定的值来代替邻域中心像素的值。其他非线性滤波器后面会讲。
语法g = ordfilt2(f, order, domain)

• 使用领域的一组排序元素中的第order来代替f中的元素。邻域由domain中的非零元素指定
• domain是由0 1组成的矩阵。且能指定具体的“邻域”。
  比如最小值滤波：g = ordfilt2(f, 1, ones(m, n))
  也有最大值滤波：g = ordfilt2(f, m * n, ones(m, n))
  当然也有中值滤波：g = ordfilt2(f, median(1:m*n), ones(m, n))
median可以按行向量求出每个行向量的中值，最后得到一个中值列向量。但。用ceil((m*n)/2)也行啊，用median还更费时间。。。