Graph Transformer Networks(图Transformer网络)
Graph Transformer Networks与2019年发表在NeurIPS上
文章目录
- 摘要
- 一、Introduction
- 二、Related Works
- 三、Method
-
- 3.1准备工作
- 3.2 Meta-Path Generation
- 3.3 Graph Transformer Networks
- Conclusion
- 个人总结
摘要
图神经网络(GNNs)已被广泛应用于图形的表示学习,并在节点分类和链路预测等任务中取得了最先进的性能。然而,大多数现有的神经网络被设计来学习固定和同构图上的节点表示。当学习由各种类型的节点和边组成的错误图或异构图的表示时,这些限制尤其成问题。在本文中,我们提出了能够生成新的图结构的Graph Transformer Networks(GTNs),包括识别原始图中未连接节点之间的有用连接,同时以端到端的方式学习新图上的有效节点表示。Graph Transformer layer是GTNs的核心层,它学习边的类型和复合关系的软选择,以生成有用的多跳连接,即所谓的元路径。我们的实验表明,GTNs学习新的图形结构,基于数据和任务,没有领域知识,并产生强大的节点表示通过卷积对新的图形。在没有特定领域的图预处理的情况下,相对于需要来自领域知识的预定义元路径的最先进的方法,GTNs在所有三个基准节点分类任务中实现了最佳性能。
一、Introduction
近年来,图神经网络(GNNs)已被广泛应用于各种图形上的任务,如图分类[11,21,40],链路预测[18,30,42]和节点分类[3,14,33]。GNNs学习的表征已经被证明在各种图形数据集上实现最先进的性能是有效的,例如社交网络[7,14,35],引用网络[19,33],大脑的功能结构[20],推荐系统[1,27,39]。底层图结构被神经网络利用,通过将节点特征[12,14]传递给邻居,直接在图上进行卷积,或者使用给定图的傅立叶基,即拉普拉斯算子[9,15,19]的特征函数,在谱域中进行卷积。
然而,大多数神经网络的一个限制是,它们假设操作神经网络的图形结构是固定的和同构的。由于上面讨论的图卷积是由固定的图结构决定的,具有缺失/虚假连接的噪声图导致与图上错误邻居的无效卷积。此外,在一些应用中,构建一个图形来操作GNNs并不容易。例如,引用网络具有多种类型的节点(例如,作者、论文、会议)和由它们的关系(例如,作者-论文、论文-会议)定义的边,并且它被称为异构图。一种天真的方法是忽略节点/边类型,并将其视为同构图(一种具有一种类型的节点和边的标准图)。这显然是次优的,因为模型不能利用类型信息。最近的补救措施是手动设计元路径,这是与异类边连接的路径,并进行变换将异构图转换为由元路径定义的同构图。然后传统的神经网络可以在变换同构图上运行[37,43]。这是一个两阶段的方法,需要为每个问题手工创建元路径。下游分析的准确性会受到这些元路径选择的显著影响。
在这里,我们开发了Graph Transformer Networks(GTN),它学习将异构输入图形转换为每个任务的有用元路径图形,并以端到端的方式学习图形上的节点表示。GTNs可视为空间变换网络的图形模拟[16],它明确学习输入图像或特征的空间变换。将异构图转换为由元路径定义的新图结构的主要挑战是元路径可以具有任意长度和边类型。例如,引文网络中的作者分类可能受益于元路径,即作者-论文-作者(APA)或作者-论文-会议论文-作者(APCPA)。此外,引用网络是有向图,其中相对较少的图神经网络可以操作。为了应对这些挑战,我们需要一种模型,该模型基于与异构图中的软选择边缘类型相关联的复合关系生成新的图结构,并通过对给定问题的已学习图结构的卷积来学习节点表示。
我们的贡献如下:(1)我们提出了一个新的框架Graph Transformer Networks,学习一个新的图结构,包括识别有用的元路径和多跳连接,以学习有效的节点表示图。(二)图生成是可解释的,模型能够提供关于预测的有效元路径的见解。(三)我们证明了由Graph Transformer Networks(学习的节点表示的有效性,相对于在异构图上的所有三个基准节点分类中额外使用领域知识的最先进的方法,产生了最佳的性能。
二、Related Works
图神经网络。近年来,已经为广泛的任务开发了许多类GNNs。它们分为两种方法:谱图方法[5,9,15,19,22,38]和非谱图方法[7,12,14,26,29,33]。基于谱图理论,布鲁纳等人[5]提出了一种利用给定图的傅里叶基在谱域执行卷积的方法。Kipf等人[19]利用谱图卷积的一阶近似简化了GNNs。另一方面,非谱方法利用空间上的近邻直接在图上定义卷积运算。例如,维克维等人[33]对不同程度的节点应用不同的权重矩阵,汉密尔顿等人[14]提出了可学习的聚集器函数,该函数为图形表示学习总结邻居的信息。
用GNNs进行节点分类。节点分类研究了几十年。传统上,手工制作的特征已经被使用,例如简单的图形统计[2],图形内核[34],以及来自局部邻居结构的工程特征[23]。这些功能不灵活,性能差。为了克服这个缺点,最近在DeepWatch[28]、LINE [32]和node2vec [13]中提出了通过图的随机游走的节点表示学习方法,这些方法采用了来自深度学习模型的技巧(例如,skip-gram),并且在性能上获得了一些改进。然而,所有这些方法仅仅基于图结构来学习节点表示。这些表示没有针对特定任务进行优化。由于CNN在表征学习方面取得了显著的成功,GNN为给定的任务和数据学习了强大的表征。为了提高性能或可扩展性,已经研究了基于谱卷积的广义卷积[4,26],对邻居的注意机制[25,33],二次采样[6,7]和大图的归纳表示[14]。虽然这些方法显示出突出的结果,但所有这些方法都有一个共同的局限性,即只处理同构图。
然而,许多现实世界的问题往往不能用一个单一的同构图来表示。这些图是一个异构的图,有各种类型的节点和边。由于大多数GNN是为单个同构图设计的,一个简单的解决方案是两阶段方法。它使用元路径作为预处理,将异构图转换为同构图,然后学习表示。metapath2vec [10]通过使用基于元路径的随机行走来学习图形表示,HAN [37]通过将异构图形转换为由元路径构建的同构图形来学习图形表示学习。然而,这些方法由领域专家手动选择元路径,因此可能无法捕获每个问题的所有有意义的关系。此外,性能可能受到元路径选择的显著影响。与这些方法不同,我们的Graph Transformer Networks可以在异构图形上运行,并为任务转换图形,同时以端到端的方式学习转换图形上的节点表示。
三、Method
我们的框架——Graph Transformer Networks的目标是生成新的图结构,并同时学习所学图上的节点表示。与大多数假设图是给定的图上CNN不同,GTN使用多个候选邻接矩阵来寻找新的图结构,以执行更有效的图卷积并学习更强大的节点表示。学习新的图结构包括识别有用的元路径,即与异构边连接的路径和多跳连接。在介绍我们的框架之前,我们简要总结了GCNs中元路径和图卷积的基本概念。
3.1准备工作
我们的框架的一个输入是具有不同类型的节点和边的多个图结构。设 T v T_v Tv和Te分别为节点类型和边类型的集合。输入图可以被视为异构图[31] G = ( V , E ) G = (V,E) G=(V,E),其中V是一组节点,E是一组具有节点类型映射函数Fv:V→Tv和边类型映射函数fe: E → Te的观察边。每个节点vi∈ V有一个节点类型,即fv(vi) ∈ Tv。同样,对于eij∈ E,fe(eij) ∈ Te。当|Te| = 1且|Tv| = 1时,它成为标准图形。本文考虑|Te| > 1的情形。设N表示节点数,即|V |。异构图可以用一组邻接矩阵{ Ak } K k =来表示,其中K = |Te|,Ak∈ RN×Ni当存在从j到I的第K型边时,Ak[i,j]是非零的邻接矩阵。更简洁地说,它可以写成张量A ∈ RN×N×K。我们还有一个特征矩阵X∈rn×D,它表示每个节点的D维输入特征。
由p表示的元路径[37]是异构图G上与异构边连接的路径,即v1 t1→v2 T2→。。。TL→VL+1,其中tl∈ Te是元路径的第l个边类型。它定义了一个复合关系R = t1♀T2。。。节点v1和v1+1之间的t1,其中R1表示关系R1和R2的组成。给定复合关系R或边类型序列(t1,t2,.。。元路径P的邻接矩阵APof通过邻接矩阵的乘法获得,如下
![]()
元路径的概念包含了多跳连接,我们框架中的新图结构由邻接矩阵表示。例如,元路径作者论文会议(APC)可以表示为A AP→P P C→C,它通过AAP和AP C的多重选择生成邻接矩阵AAP Cbc。
图卷积网络(GCN)。在这项工作中,图卷积网络(GCN) [19]被用来学习端到端方式的节点分类的有用表示。设H(l)为格网第1层的特征表示,则前向传播变为
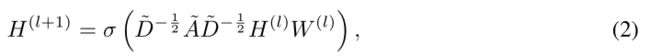
其中,A = A + I ∈ RN×N是图G的自连接增加后的邻接矩阵A,D是A的度矩阵,即Dii = P I∈Aij,W(l)∈ Rd×d是可训练权重矩阵。人们可以很容易地观察到,图中的卷积运算是由给定的图结构决定的,除了节点线性变换H(l)W(l)之外,它是不可学习的。因此,卷积层可以解释为一个固定卷积的组合,然后是图中的激活函数σ,经过节点线性变换。因为我们学习图结构,所以我们的框架受益于不同的卷积,即从学习的多个邻接矩阵˜D−12˜A˜D−12获得的。该架构将在本节稍后介绍。对于一个有向图(即非对称邻接矩阵),式(2)中的≘A可以用度内对角矩阵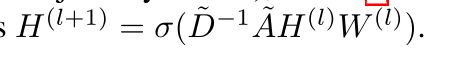
来归一化。
3.2 Meta-Path Generation
以前的工作[37,43]需要手动定义元路径,并在元路径图上执行图神经网络。相反,我们的Graph Transformer Networks(GTNs)为给定的数据和任务学习元路径,并在学习的元路径图上操作图卷积。这提供了找到更有用的元路径的机会,并使用多个元路径图来产生各种各样的图卷积。
图1中Graph Transformer GT)层中新的元路径图生成有两个组件。首先,GT层从候选邻接矩阵A中轻轻地选择两个图结构Q1和Q2。其次,它通过两个关系的组合(即两个邻接矩阵Q1Q2的矩阵乘法)学习一个新的图结构。
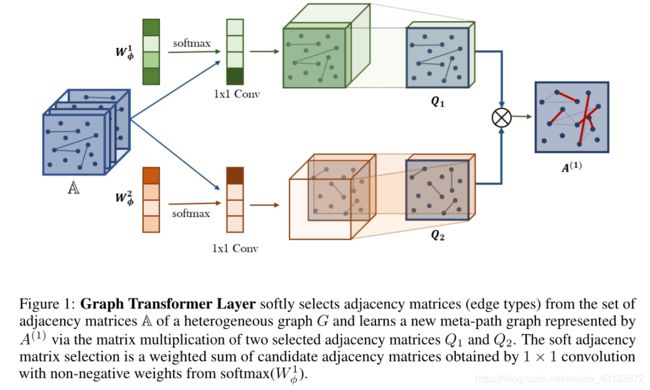
它通过1×1卷积计算邻接矩阵AsP t1∈Teα(l)tlAtlin(4)的凸组合,如图1所示,来自softmax函数的权重为
![]()
其中φ是卷积层,Wφ∈ R1×1×K是φ的参数。这个技巧类似于[8]中低成本图像/动作识别的通道注意力集中。给定两个软选择邻接矩阵Q1Q2和Q2,元路径邻接矩阵通过矩阵乘法Q1q 2计算。为了数值稳定性,矩阵通过其度矩阵归一化为A(l)= d1q 1q 2。
现在,我们需要检查GTN是否能够学习关于边类型和路径长度的任意元路径。任意长度l元路径的邻接矩阵可以通过下式计算
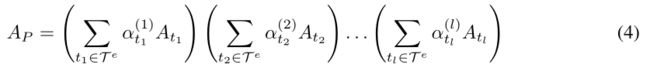
其中,α表示元路径的邻接矩阵,Te表示一组边类型,α(l)是第1层GT层边类型的权重。当α不是单热向量时,AP可以看作所有长度为l的元路径邻接矩阵的加权和。因此,l个GT层的堆叠允许学习任意长度的l元路径图结构,如图2所示的GTN体系结构。这种构造的一个问题是,添加GT层总是增加元路径的长度,这不允许原始边。在某些应用中,长元路径和短元路径都很重要。为了学习包括原始边在内的短元路径和长元路径,我们包括了同一性A中的矩阵I,即A0= I。当堆叠l个GT层时,该技巧允许GTN学习高达l + 1的任意长度的元路径。
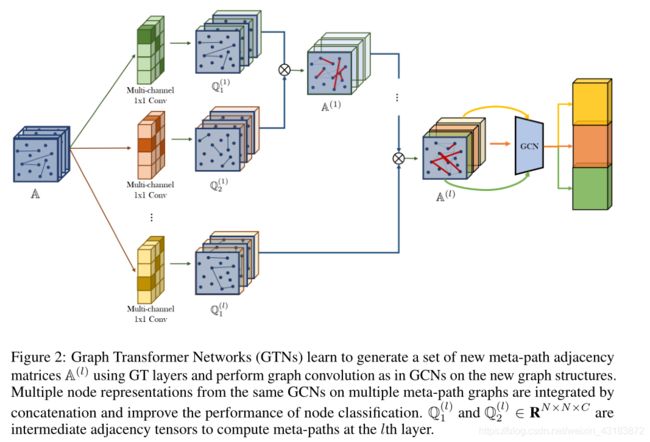
3.3 Graph Transformer Networks
这里我们介绍Graph Transformer Networks的体系结构。为了同时考虑多种类型的元路径,图1中1×1卷积的输出通道被设置为C。然后,GT层产生一组元路径,中间邻接矩阵Q1和Q2成为图2中的邻接张量Q1和Q2∈ RN×N×C。通过多个不同的图结构学习不同的节点表示是有益的。在堆叠l个层之后,将GCN应用于元路径张量A(l)∈ RN×N×C的每个通道,并且将多个节点表示连接为

其中,||是连接运算符,C表示通道数,I = I+I是从A(l)的第一个通道开始的邻接矩阵,Diis是A(l) i的度矩阵,W∈Rd×d是跨通道共享的可训练权重矩阵,X∈RN×d是特征矩阵。z包含来自不同元路径图的节点表示,长度可变,最多l + 1。它用于顶部的节点分类,并使用两个密集层和一个softmax层。我们的损失函数是一个标准的交叉熵,在节点上有基本真理标签。这种体系结构可以被看作是由成组层学习的多个元路径图上的一个集合。
Conclusion
我们提出了用于学习异构图上节点表示的Graph Transformer Networks。我们的方法将异构图转换为由元路径定义的多个新图,元路径具有任意边类型和任意长度,最多比图转换器层数少一层,同时它通过对学习的元路径图进行卷积来学习节点表示。学习的图结构导致更有效的节点表示,从而在异构图上的所有三个基准节点分类上产生最先进的性能,而没有来自领域知识的任何预定义元路径。由于我们的Graph Transformer 层可以与现有的图神经网络相结合,我们相信我们的框架为图神经网络自己优化形结构开辟了新的途径,以便根据数据和任务进行卷积,而无需任何手动操作。感兴趣的未来方向包括研究与不同类别的神经生长因子结合的神经生长因子层的功效,而不是神经生长因子。此外,由于最近针对其他网络分析任务研究了几个异构图形数据集,如链接预测[36,41]和图形分类[17,24],将我们的几何网络应用于其他任务可能是有趣的未来方向。
个人总结
需要多看两遍,细品。。。。。。