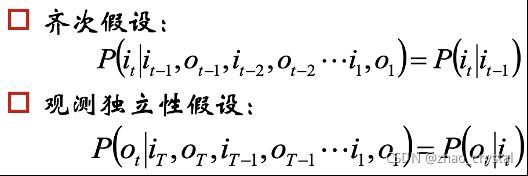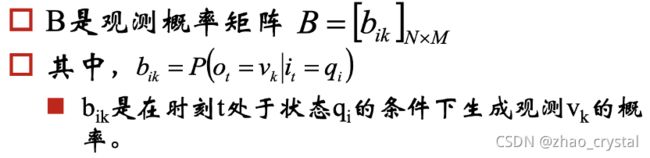隐马尔科夫模型（HMM）
目录
1.隐马尔科夫模型求解步骤（其它大部分模型也均遵循如下路径）
2. HMM定义
2.1 HMM的两个基本性质
2.2 HMM的确定
3. HMM的三个基本问题
3.1 概率计算问题
3.1.1直接计算（暴力算法）
3.1.2前向算法和后向算法
3.2 参数估计/学习
3.2.1若训练数据包括观测序列和状态序列，则HMM的学习非常简单，是监督学习
3.2.2若训练数据只有观测序列，则HMM的学习需要使用EM算法，是非监督学习
3.3 模型的预测
3.3.1预测的近似算法
3.3.2 Viterbi算法
4. HMM的应用——中文分词
5. HMM总结
6.GMHMM
7. 参考文献
隐马尔科夫模型，Hidden Markov Model，缩写HMM
1.隐马尔科夫模型求解步骤（其它大部分模型也均遵循如下路径）
概率计算
参数估计
模型预测
这里以logistic回归为例，具体说一下以上三个过程
2. HMM定义
（1）隐马尔科夫模型可用于标注问题，在语音识别，NLP，生物信息，模式识别等领域被实践证明是有效的算法。
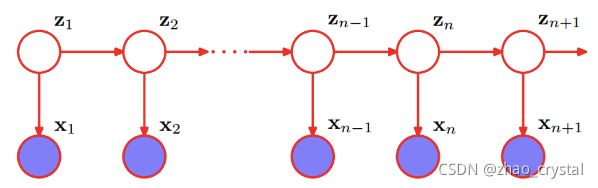
（2）HMM是关于时序的概率模型，描述由一个隐藏的马尔科夫链生成不可观测的状态随机序列，再由各个状态生成观测随机序列的过程。
（3）隐马尔科夫模型随机生成的状态随机序列，称为状态序列；每个状态生成的一个观测，由此产生的观测随机序列，称为观测序列。
序列的每个位置可看作是一个时刻。
其中，在z1，z2不可观察的前提下，x1和z2不独立，x1和x2也不独立，即观测序列x1，x2，……xn是结构化的。结构化的空间连续或时间连续的数据，就可以尝试使用HMM。
2.1 HMM的两个基本性质
假设状态序列为：
，观测序列为
2.2 HMM的确定 
HMM可以用三元符号表示，称为HMM三要素：
3. HMM的三个基本问题
3.1 概率计算问题
3.1.1直接计算（暴力算法）
3.1.2前向算法和后向算法
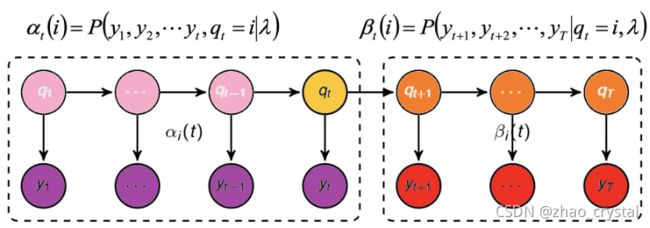
定义前向概率——后项概率
（1）前向算法
（2）后向算法
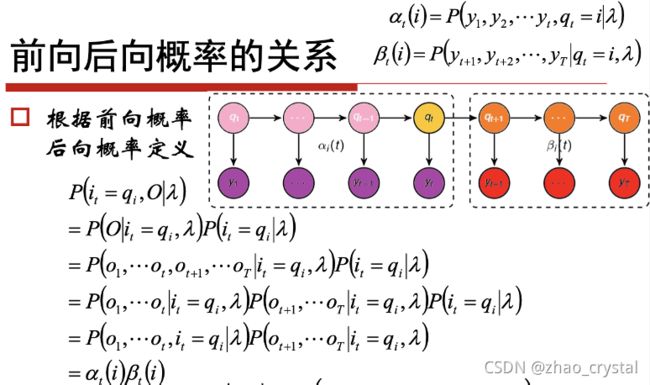
（3）前向后向概率的关系
单个状态的概率
两个状态的联合概率
3.2 参数估计/学习
3.2.1若训练数据包括观测序列和状态序列，则HMM的学习非常简单，是监督学习
大数定理
假设已给定训练数据包含S个长度相同的观测序列和对应的状态序列{(O1,I1), (O2,I2), ……(O3,I3)}, 那么可以直接利用Bernoulli大数定理的结论“频率的极限是概率”，给出HMM的参数估计。
3.2.2若训练数据只有观测序列，则HMM的学习需要使用EM算法，是非监督学习
3.3 模型的预测
求出参数λ ，有观测值o，求隐变量。
3.3.1预测的近似算法
3.3.2 Viterbi算法
Viterbi算法实际是用动态规划解HMM预测问题，用DP求概率最大的路径（最优路径），这是一条路径对应一个状态序列。
定义变量δt(i) :在时刻t状态为i的所有路径中，概率的最大值。
4. HMM的应用——中文分词
状态序列{Begin, Middle, End, single}, 表示的意思分别是一个词的开始，中间，结束，但字成词。
观测序列{0,1,2,……65535}表示共有0——65535个字
可以用如下已经分词好的文章，计算λ=(π,A,B) , 训练数据包括观测序列和状态序列,用大数定理计算参数
注意1：防止概率越乘越小，导致下溢出，故使用对数来解决这个问题
初始概率：
，同理，转移概率和观测概率也均需求对数。
以上可叫做对数正则。
注意2: Pi 只要统计一句话的第一个字。且一句话的第一个字肯定不是Middle 和 End，只有可能是Begin 和single。
5. HMM总结
(1)马尔科夫模型可以用来同意解释贪心法和动态规划
(2)HMM解决标注问题，在语音识别，NLP，生物信息，模式识别等领域被广泛应用。
思考：可否使用深度学习代替HMM
思考：如果观测状态是连续值，可否将多项分布改成高斯分布或者混合高斯分布。
(3) HMM是一个生成模型
6.GMHMM
HMM要求和状态序列是离散的，观测值不要求是离散，若观测值连续，且符合高斯分布，则——>高斯分布隐马尔科夫模型。
