多通道语音增强笔记

多通道语音增强笔记

1. 固定波束形成：利用阵列对特定方向进行波束增强（即目标语音方向），若噪声和目标语音同向，则无显著效果。

   • 麦克风接受信号：$Y_m(\omega ,\theta )=H_m(\omega ,\theta )\ast exp(-k\omega {\tau }_m(\theta ))\ast S(\omega )$

     $H_m$是麦克风的指向性，${\tau }_m$是麦克风时延带来的在频域是上的延迟，$S(\omega )$是原信号，上式可写为：

     $Y(\omega ,\theta )=d(\omega ,\theta )\ast S(\omega )$，$d(\omega ,\theta )=[H_1(\omega ,\theta )exp(-j{\tau }_1(\theta )),...,H_M(\omega ,\theta )exp(-j{\tau }_M(\theta ))]$为导向向量，当麦克风为全指向性时，$H$全都为1

   • 麦克风经滤波后的输出信号：$Z(\omega ,\theta )=F^H(\omega ,\theta )Y(\omega ,\theta )=F^H(\omega )d(\omega ,\theta )S(\omega )$，$F$为滤波器

   • 性能指标：

     • 噪声增益：$G(\omega ,\theta )=\frac{SN{R}_o}{SN{R}_i}=\frac{|F^{H}d(\omega ,\theta ){|}^2}{F^H(\omega ){\Gamma }_{noise}F(\omega )}$，若为白噪则${\Gamma }_{noise}=I$

     • 指向性：$DI(\omega ,\theta )=\frac{|F^{H}d(\omega ,\theta ){|}^2}{F^H{\Gamma }_{noise}^{diffuse}F(\omega )}$

     • 通常我们可以最大化白噪声增益，即：$F(\omega )=\arg \max \frac{|F^{H}d(\omega ,\theta ){|}^2}{F^H(\omega )F(\omega )}$，可将问题转化为：
       $$F(\omega )=\arg \min F^H(\omega )F(\omega )s.t.|F^H(\omega )d(\omega ,\theta )=1|$$
       也即期望方向信号增益为0 dB，并最小化噪声输出，最优解为$F(\omega )=\frac{d(\omega ,\theta )}{|d(\omega ,\theta ){|}^2}$

     • 对于一般噪声，其解为：$\frac{{\Gamma }^{-1}d(\omega ,\theta )}{d^H(\omega ,\theta ){\Gamma }^{-1}d(\omega ,\theta )}$，$\Gamma$表示噪声相关阵

   • 固定波束的系数是提前计算好的，不需要进行系数更新，计算速度快

2. 后滤波器算法：使用一个维纳系数$w_{post}$进一步一直波束形成算法中的残留非点源噪声，即$\hat{Z}(\omega ,\theta )=w_{post}{F}^H(\omega )Y(\omega ,\theta ),w_{post}=\frac{{\sigma }_s^2(\omega ,\theta )}{{\sigma }_s^2(\omega ,\theta )+{\sigma }_n^2(\omega ,\theta )}$，${\sigma }_s^2(\omega ,\theta )$和${\sigma }_n^2(\omega ,\theta )$分别代表目标语音信号和噪声的功率谱密度，问题的关键在于：如何让利用多通道信号求解上述功率谱密度

   • Zelinski等人在论文中的求解：
     $$\begin{gathered} {\sigma }_s^2(\omega ,\theta )=\frac{2}{M(M-1)}\sum _{i=1}^{M-1}\sum _{j=i+1}^M\mathcal{R}\{{\hat{\varphi }}_{y_i{y}_j}(\omega ,\theta )\} \\ {\sigma }_n^2=[\frac{1}{M}\sum _{i=1}^M{\hat{\varphi }}_{y_i{y}_j}(\omega ,\theta )]-{\sigma }_s^2(\omega ,\theta )] \end{gathered}$$
     在时频域表示：${\hat{\varphi }}_{y_i{y}_j}(t,f)=\alpha {\hat{\varphi }}_{y_i{y}_j}(t-1,f)+(1-\alpha )y_i(t,f)y_j^{\ast }(t,f)$为观测信号的互功率谱密度$(i\ne j)$或自功率谱密度$(i=j)$，$\mathcal{R}$为取实部操作

   • McCowan等人针对散射噪声的求解：
     $$\begin{gathered} {\sigma }_s^2(t,f)=\frac{2}{M(M-1)}\sum _{i=1}^{M-1}\sum _{j=i+1}^M\Theta (t,f) \\ {\sigma }_n^2(t,f)=[\frac{1}{M}\sum _{i=1}^M{\hat{\varphi }}_{y_i{y}_j}(t,f)-{\sigma }_s^2(t,f)] \end{gathered}$$
     其中$\Theta =\frac{\mathcal{R}\{{\hat{\varphi }}_{y_i{y}_j}(t,f)\}-\frac{1}{2}{\gamma }_{ij,diffuse}(f)({\hat{\varphi }}_{y_i{y}_i}(t,f)+{\hat{\varphi }}_{y_j{y}_j}(t,f))}{1-{\gamma }_{ij,diffuse}(f)}$

   • 不足：后滤波器算法可能会像单通道维纳滤波一样引入频谱损伤

3. 多通道线性预测算法：一种用于降混响的算法

   • 其在STFT域下的信号模型如下：$y_1(t)=x_1(t)+c^H{y}_{\tau ,L_c}(t)$，$y_1(t)$为第一个麦克风的观测信号，$x_1(t)$为第一个麦克风的目标语音信号。$y_{\tau ,L_c}$为历史观测向量（含全部麦克风）。$c$为滤波器系数向量（对每个频带单独处理，忽略索引$f$）。即若估计出$c$便可得到降混响后的语音信号$x_1(t)$

   • Naktani等人对$c$的估计，假设目标语音服从高斯分布，利用最大似然估计$c$：
     $$c={\mathrm{argmin}}_c\sum _{t=1}^T\frac{|y_1(t)-c^H{y}_{\tau ,L_c}^T(t){|}^2}{{\sigma }_x^2(t)}$$
     但是以此式难以求得$c$的解析解，因此常用迭代交替更新$c$和${\sigma }_x^2$：

     • 初始化${\sigma }_x^2=\max \{|y_1^2(t)|,ϵ\}$

     • 重复下列操作直至收敛：
       $$\begin{gathered} (1)c=[\sum _{t=1}^T\frac{y_{\tau ,L_c}(t)y_{\tau ,L_c}^T(t)}{{\sigma }_x^2(t)}{]}^{-1}\sum _{t=1}^T\frac{y_{\tau ,L_c}(t)y_1^T(t)}{{\sigma }_x^2(t)} \\ (2)x_1(t)=y_1(t)-c^H{y}_{\tau ,L_c}(t) \\ (3){\sigma }_x^2=\max \{|x_1^2(t),ϵ|\} \end{gathered}$$

4. MVDR：最小无失真响应（Minimum Variance Distortionless Response）

   和固定波束算法思路类似，但是其具有自适应能力，即可通过空间扫描来寻找出功率最强的方向

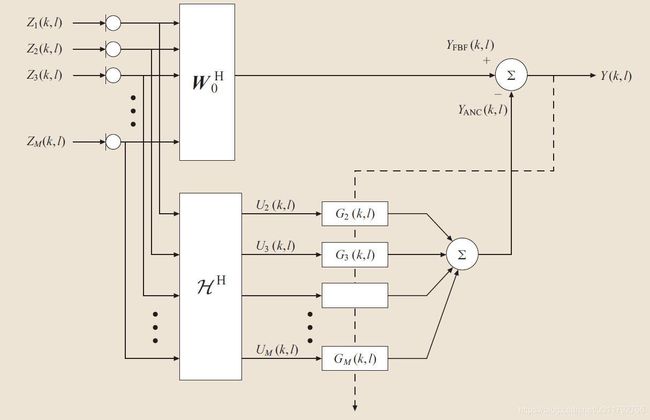
5. 广义旁瓣相消：是MVDR的另一种形式，两者已经在数学上被证明是等价的：

   

   其中$W_0$为固定波束，$\mathcal{H}$是分块矩阵，$G$是自适应的噪声抵消器，虚线即自适应过程，论文中的表述为：
   $$w_{gsc}=w_{dsb}(t,f)-N(t,f)w_{nc}(t,f)$$
   其中$w_{dsb}(t,f)=\frac{h(t,f)}{||h(t,f)|{|}^2},w_{nc}(t,f)=(N^H(t,f)R_n(t,f)N(t,f){)}^{-1}{N}^H(t,f)R_n(t,f)w_{dsb}(t,f)$

   $w_{dsb}$为延时求和的股东波束形成器，$N(t,f)$是一个阻塞目标信号的阻塞矩阵，$w_{nc}(t,f)$为噪声抵消器

6. LCMV：线性约束最小方差：在满足条件的情况下使输出功率最小，也即方差最小：
   $$J=\sum _{k=0}^{M-1}\sum _{i=0}^{M-1}{w}_k^{\ast }{w}_{i}r(i-k)+Re[{\lambda }^{\ast }(\sum _{k=0}^{M-1}{w}_k^{\ast }{e}^{-j{\theta }_{0}k}-g)]$$
   $w$为波束形成器的权值，需要最小化$J$，使用Lagrange乘子法：${\nabla }_{k}J=2{\sum }_{i=0}^{M-1}{w}_{i}r(i-k)+{\lambda }^{\ast }{e}^{-j{\theta }_{0}k}$，令$w_{o,i}$为最优权向量第$i$个元素则波束形成器最优性条件描述为：
   $$\sum _{i=0}^{M-1}{w}_{o,i}r(i-k)=-\frac{{\lambda }^{\ast }}{2}{e}^{-j{\theta }_{0}k},k=0,1,...,M-1$$
   矩阵形式为：
   $$R{w}_0=-\frac{{\lambda }^{\ast }}{2}s({\theta }_0),s({\theta }_0)=[1,e^{-j{\theta }_0},...,e^{-j(M-1){\theta }_0}{]}^T$$
   可得$w_o=-\frac{{\lambda }^{\ast }}{2}{R}^{-1}s({\theta }_0)(\ast )$，其中$R$为接收信号的相关矩阵（非奇异），由线性约束条件$w_o^{H}s({\theta }_0)$对$(\ast )$两边进行Hermite变换，再乘以$s({\theta }_0)$，利用上式可得：
   $$\lambda =-\frac{-2g}{s^H({\theta }_0)R^{-1}s({\theta }_0)}$$
   最终得到：
   $$w_o=\frac{g^{\ast }{R}^{-1}s({\theta }_0)}{s^H({\theta }_0)R^{(}-1)s({\theta }_0)}$$
   由于是再约束条件下使输出功率最小，故沿不同于${\theta }_0$方向上的信号会被削弱，此被称为线性约束最小方差(LCMV)波束形成器

   • 亦可引出MVDR：$g=1$时，$w_o=\frac{R^{-1}s({\theta }_0)}{s^H({\theta }_0)R^{-1}s({\theta }_0)}$，沿着对应于${\theta }_0$的方向产生无失真响应，此时$J_{min}=w_o^{H}R{w}_o$将$w_o$代入有：$J_{m}in=\frac{1}{s^H(\theta )R^{-1}s(\theta )}$，将$J_{min}$表示为$\theta$的函数，推广此结果并获得以方向为变量的方差估值函数，MVDR的（空间）功率谱为：
     $$S_{MVDR}=\frac{1}{s^H({\theta }_0)R^{-1}s({\theta }_0)},s(\theta )=[1,e^{-j\theta },...,e^{-j(M-1)\theta }]$$

   • 《自适应滤波器原理》中的广义旁瓣相消如下，其中$w_q$是权向量$w$满足约束条件的部分，$w_a$是不受约束的部分，提供了滤波器设计的自由度，$w_q$类似固定的约束无失真响应滤波器，$C_a$为信号阻塞矩阵，阻断了角频率处的接收信号，其功能是消除静态权向量为$w_q$的带通滤波器旁瓣渗透出的干扰

   

7. 盲源分离：观测信号由多种未知信号混合而成，想要将这些信号分离，例子：
   $$\begin{gathered} x_1(t)=a_{11}{s}_1(t)+a_{12}{s}_2(t)+a_{13}{s}_3(t) \\ {x}_2(t)=a_{21}{s}_1(t)+a_{22}{s}_2(t)+a_{23}{s}_3(t) \\ {x}_3(t)=a_{31}{s}_1(t)+a_{32}{s}_2(t)+a_{33}{s}_3(t) \end{gathered}$$
   其中$x$为观测信号，$s$为源信号，若系数矩阵是可逆的，则：
   $$\begin{gathered} s_1(t)=w_{11}{x}_1(t)+w_{12}{x}_2(t)+w_{13}{x}_3(t) \\ {s}_2(t)=w_{21}{x}_1(t)+w_{22}{x}_2(t)+w_{23}{x}_3(t) \\ {s}_3(t)=w_{31}{x}_1(t)+w_{32}{x}_2(t)+w_{33}{x}_3(t) \end{gathered}$$
   独立假设：若信号非高斯，课决定$w$使得$y_i=w_{i1}{x}_1(t)+w_{i2}{x}_2(t)+w_{i3}{x}_3(t)$之间是统计独立的，则可认为源信号是统计独立的

   • 独立成分分析（ICA）：$X=AS$，只知道观测样本$X$，在源信号$S$和混合矩阵$A$未知的条件下，假设源信号$s_i$之间统计独立，来求解混合矩阵$A$和源信号$S$

     • 假设条件：

       a. 各个成分之间是统计独立的

       b. 独立成分是服从非高斯分布的（只允许一个成分副总高斯分布，若有两个及以上则无法分离）

       c. 假设混合矩阵是方阵

     • 无法确定的因素：不能确定独立成分的方差和能量，不能确定独立成分顺序

     • ICA有许多不同的算法

   b. 独立成分是服从非高斯分布的（只允许一个成分副总高斯分布，若有两个及以上则无法分离）

   c. 假设混合矩阵是方阵

   • 无法确定的因素：不能确定独立成分的方差和能量，不能确定独立成分顺序

   • ICA有许多不同的算法