基于Python的一个疫情传播可视化模拟实验
大家好!
新冠疫情已经持续有快两年了,给大家的工作和生活都带了极大的影响。在疫情之初,我曾经看到过一个对疫情传播发展的可视化模拟。现在回头看,确实如模拟中所示,只要疫情没完全消除,都存在再度传播的风险。但在各项防疫措施和全民协作之下,疫情得到了有效控制,并没有发生所模拟的最坏情况。
今天在这里给大家分享一下这个案例,既是一个数据可视化的不错学习案例,也再次提醒大家,疫情仍未结束,打疫苗、戴口罩、少聚集,坚持到底。
本案例来自公众号:Crossin的编程教室,之前被人民日报转载过。作者 Crossin 做 Python 方面的教程和案例文章已经有8年多了,在知乎上的回答累计有十多万赞,在他那儿入了 Python 门的人,加起来估计得有好几万。如果有想学习用Python做数据分析的朋友,可以点击上方的公众号链接关注一波。
这一个月来,大家最关注的就是新冠病毒疫情的发展了。令人欣慰的是,最近国内不少省市都没有新增确诊病例甚至病例数“清零”,已调低了防控级别,逐步复工复产。(编者注:文中指2020年2月)
这时我发现,在朋友圈中分化出了两种截然不同的观点:
一种认为,病毒还没完全消失,这时候就出门,很可能带来第二次传播,所以应该继续延续之前的封闭式管理;
而另一种则认为,目前湖北以外地区的疫情已基本得到控制,风险已经不高,而如果继续限制出行则会给经济带来更大的损失,应该放开管控。
这两个观点我个人觉得都有道理但都不能走极端。既没有必要过度恐慌,也不能对防控麻痹大意。尤其现在国外疫情扩散的情况下,我们更要注意潜在的风险。
这段时间在家里,我也自己做了一个模拟人群行为和病毒传播过程的程序,或许可以给大家一些参考。(代码获取方式见文末)
1. 出行模型
在流行病学中,已经有一些成熟的模型和公式。但我并非相关专业人士,所以我并没有套公式,而是用了一种简单粗暴的方法:模拟群体中每一个人的行为。
这个模型的基本要素是区域和人,这里是10万个人分布在1万个区域上的效果。图上点的大小反应了这一区域里人数的多少。考虑到现实中人群不是均匀分布的,这里我们让80%的人集中在了中间25%的区域中。
然后,让其中的每一个人都移动起来。我给这个二次元世界的人们设定了这样的规则:
1. 在每个时间段中,有一定概率会出行,否则将留在原地。这个概率我们称之为出行意愿,可以在程序中修改。对应现实中,我们上班、上学、逛街、坐公交、去饭馆,都是一种出行,都会在某个时刻与一群人在同一个区域
2. 每个人会有3~6个常驻区域,在出行时,会有大概率在常驻区域中移动,但也有一定几率会去新区域。这就好比,大多数人主要在办公室、食堂、公交、家等几个固定区域移动,同时也不可避免去其他一些地方
3. 如果去新区域,那么大概率会在周边一格区域;但也有一定几率会去随机位置。对于随机位置,你可以理解为火车、飞机等长途交通,现代人有可能在一天之内去到世界上任何一座大城市。
基于上述规则,我们的世界就动起来了。为了方便确认,我们标记出3个人,来观察下他们的行为是否符合预期
大部分时候,每个人都会在邻近的几个区域移动,偶尔也会出个远门。
2. 传染模型
定义了人的行为,我们还要来定义另一个主角:病毒。我们设定如下规则:
1. 疾病具有一定的潜伏期和发病期,潜伏期无症状,难以识别。但潜伏期不代表没有传染性,所以我们会用另一个参数来设定传染期的开始时间
2. 在每个时间点上,人们会接触部分同区域的人,处在传染期的人就有一定几率传染给其他接触者。
3. 随着时间推进,被感染的人会依次经历潜伏期、发病期。发病期有一定几率会发展成重症,重症则有一定几率会导致病亡。
4. 我们假定这些基本都是可自愈的。如果能坚持到发病期结束,则会康复。
这其中牵涉的各环节几率,我们都可以在程序的开始处设定好。
潜伏期分布 = (5, 2) # 正态分布
发病期分布 = (10, 3) # 正态分布
传染起始日 = -1 # 以潜伏期结束为基准
传播概率 = 0.5
免疫概率 = 0.1
重症概率 = 0.05
病亡概率 = 0.1说明:因为代码中用到的参数很多,为了便于理解,我把所有参数变量都用了中文命名。
首先尝试设定潜伏期为5天左右,发病期为10天左右,在潜伏期结束前一天具备传播性的情况。
我们用颜色来标记一个地区的整体情况,红色表示感染的人群的比例,绿色表示康复人群的比例
可以看到整个地图上经历了从最初小范围转播,到大面积爆发,再到逐步自愈康复的过程。
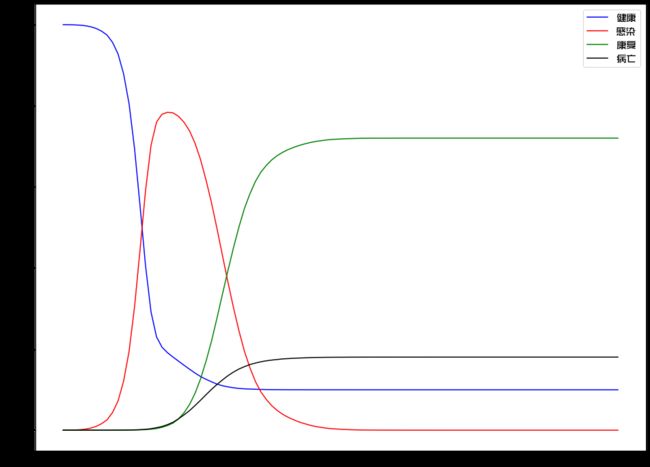
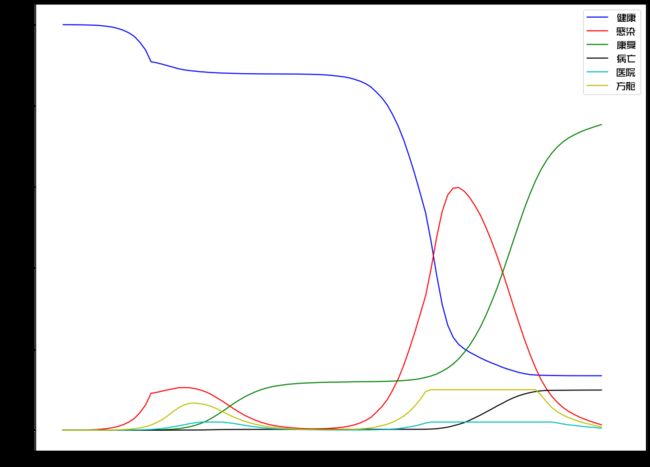
统计每个时间点上不同状况人群的数量,绘制出这样几条曲线:
其中蓝色为健康人群、红色为被感染者、绿色为康复人群、黑色则是不幸病亡人的数量。虽然我没有设定任何数学公式,但这一曲线的形态与流行病学的经典模型是相符合。这也从侧面验证了我们的模拟具备一定的可参考性。
【模拟参数】
潜伏期分布 = (5, 2)
发病期分布 = (10, 3)
传染起始日 = -1
传播概率 = 0.5
免疫概率 = 0.1
重症概率 = 0.05
病亡概率 = 0.1
戴口罩意愿 = 0
出行意愿 = 0.8
接触比例 = 0.5
入院意愿 = 0.1
【模拟结果】
被感染:72019
病亡:18018
病亡率:20.0%
在这个比较粗放的模型中,如果不加以干预任其发展,最后除了我们预先设定了一定比例的天然免疫人群外,其余人最终都会被全部传染。最终的病亡人数就单纯取决于该疾病的致命性。这在现实中自然是不可能的。
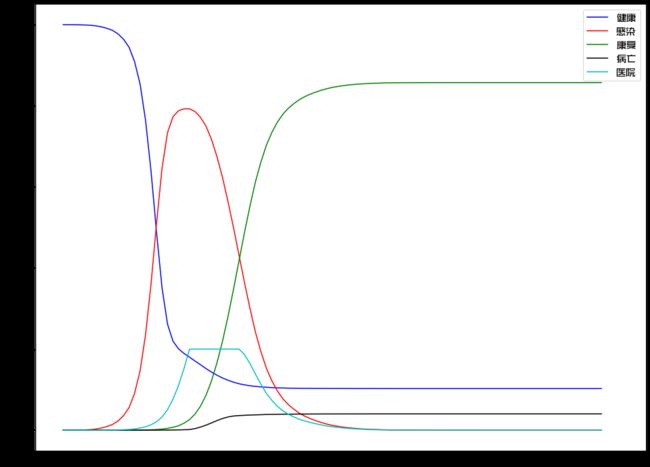
于是,我们再给这个模型增加额外的参数:医院
在这个世界中,我们增加2万张床位。当一个人有了发病表现之后,就很可能去医院就医。一旦进入医院,那么他将不再出行,同时病亡的可能性将大大下降。
再次模拟运行后可以看出,如果有充足的医疗资源,病亡率低很多。
【模拟参数】
医院床位 = 20000
入院意愿 = 0.1
救治概率 = 0.95
其他同上
【模拟结果】
被感染:85867
病亡:3944
病亡率:4.4%
但是!
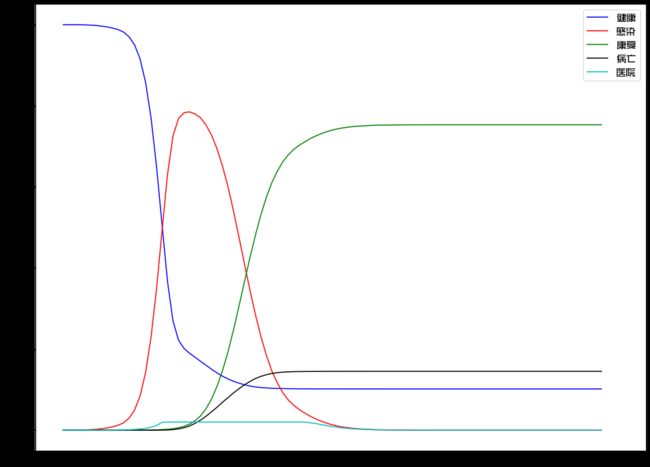
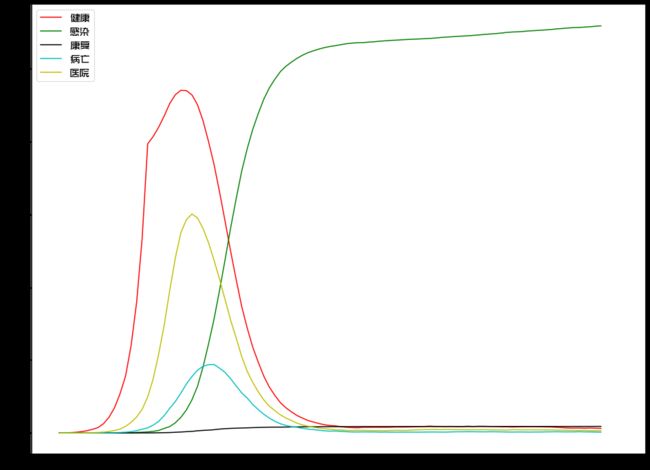
在现实中,医疗资源是有限的,当遭遇到传播性强、甚至潜伏期无症状时就会传播的疾病,医疗资源会在短期内迅速耗尽,失去对疫情的控制:
【模拟参数】
医院床位 = 2000
其他同上
【模拟结果】
被感染:80901
病亡:8956
病亡率:10.0%
3. 防控模型
所以,抗疫不能仅靠医院。当发病人数达到一定阈值之后,我们开启防控模式:
1. 大幅降低人群的出行意愿,并减少同一区域的人群接触比例
2. 让大多数人带上口罩,降低传播几率
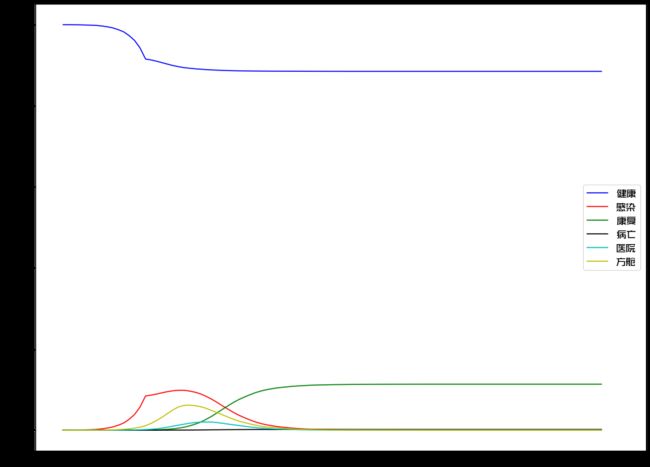
3. 另外很重要的一点是,增加方舱这个设定:将所有发病人员尽可能收入方舱,阻止进一步传播;同时也把有限的医院资源留给重症病人
在多措并举的努力下,可大大抑制疫情的扩散。
【模拟参数】
医院床位 = 2000
方舱床位 = 10000
警戒人数 = 1000
戴口罩意愿 = 0.9
出行意愿 = 0.2
接触比例 = 0.2
入院意愿 = 1
其他同上
【模拟结果】
被感染:11343
病亡:173
病亡率:1.5%
4. 放松警惕
那么,是否到了可以放松的时候呢?
如果现在我们稍稍改动一下程序,在进展到40天之后,把人们的出行意愿、戴口罩意愿、接触几率都恢复到平常的水准。那么,疫情将会再次出现一波扩散。这还是考虑到已康复人不会再次感染的情况。真实情况下,潜在的风险可能更大。
【模拟参数】
解除时间 = 40
其他同上
【模拟结果】
被感染:76083
病亡:9901
病亡率:11.5%
所以啊,万不可放松警惕,复工复产很重要,也要记得戴口罩,开窗通风勤洗手,别往人多地方跑。
即便不继续维持之前高级别的防控措施,我们只要保证大多数人还在戴口罩,适当降低不必要的外出,那么疫情就会得到有效的控制。并非一定要休克式的严防死守。在做好重点地区疫情防控的前提下,相对安全地区的人做好个人防护,有序复工才是更加可持续的应对方式。
【模拟参数】
解除时间 = 40
戴口罩意愿 = 0.9
出行意愿 = 0.8
接触比例 = 0.5
入院意愿 = 1
其他同上
【模拟结果】
被感染:11212
病亡:181
病亡率:1.6%
以上就是对疫情的可视化模拟。
经过近两年的持续努力,我们已经对疫情防控有了更多的认识,加上疫苗的普及,可以说已经基本控制住了疫情。但毕竟疫情仍未结束,部分地区还出现零星传播病例。所以仍不可大意,需要我们继续努力,理性抗疫,齐心协力,共克时艰。
文中案例的详细参数和模拟逻辑,大家可结合代码来理解。建议使用 Jupyter 来运行代码。
获取代码请在公众号(Crossin的编程教室)里回复关键字 病毒
Crossin还有很多寓教于乐的有趣教学文章,涉及数据分析、Web开发、游戏开发、微信小程序、图像处理等领域,欢迎大家关注:
如何用100行Python代码做出魔性声控游戏“八分音符酱”
Python有嘻哈:Crossin教你用代码写出押韵的verse
弹幕君,别挡着我看小姐姐!
王校长一分钟能吃多少热狗?| 小游戏
用 Python 实现抖音尬舞机
一段蛋疼的代码:超不清视频播放器
用python模拟地球飞越木星