【建模算法】Python调用scikit-opt工具箱中的遗传算法求解TSP问题

【建模算法】Python调用scikit-opt工具箱中的遗传算法求解TSP问题

TSP (traveling salesman problem，旅行商问题)是典型的NP完全问题，即其最坏情况下的时间复杂度随着问题规模的增大按指数方式增长，到目前为止还未找到一个多项式时间的有效算法。本文探讨了Python调用scikit-opt工具箱中的遗传算法求解TSP问题。

一、问题描述

​ 本案例以31个城市为例，假定31个城市的位置坐标如表1所列。寻找出一条最短的遍历31个城市的路径。

城市编号	X坐标	Y坐标	城市编号	X坐标	Y坐标
1	1.304	2.312	17	3.918	2.179
2	3.639	1.315	18	4.061	2.37
3	4.177	2.244	19	3.78	2.212
4	3.712	1.399	20	3.676	2.578
5	3.488	1.535	21	4.029	2.838
6	3.326	1.556	22	4.263	2.931
7	3.238	1.229	23	3.429	1.908
8	4.196	1.044	24	3.507	2.376
9	4.312	0.79	25	3.394	2.643
10	4.386	0.57	26	3.439	3.201
11	3.007	1.97	27	2.935	3.24
12	2.562	1.756	28	3.14	3.55
13	2.788	1.491	29	2.545	2.357
14	2.381	1.676	30	2.778	2.826
15	1.332	0.695	31	2.37	2.975
16	3.715	1.678

二、scikit-opt工具箱简介

scikit-opt工具箱是一个封装了7种启发式算法的 Python 代码库，包含差分进化算法、遗传算法、粒子群算法、模拟退火算法、蚁群算法、鱼群算法、免疫优化算法。官网链接：https://scikit-opt.github.io/scikit-opt/#/zh/

三、调用scikit-opt工具箱中遗传算法求解TSP问题的步骤

1.安装工具箱

pip install scikit-opt

2.编写自定义问题

主要是将自己问题的数据输入到封装的代码中，操作简单，修改码量很少
其中只有两行代码需要修改

num_points = 30                #num_points指需要遍历的节点个数
points_coordinate = np.random.rand(num_points, 2)    #points_coordinate是自定义问题中的节点坐标信息

3.调用遗传算法进行求解

其中的best_points表示最短距离的num_points点的序列（即points_coordinate矩阵中第几个点，但没有回到起点）

from sko.GA import GA_TSP

ga_tsp = GA_TSP(func=cal_total_distance, n_dim=num_points, size_pop=50, max_iter=500, prob_mut=1)
best_points, best_distance = ga_tsp.run()

4.绘制近似最优路径图像

其中的best_points_ 表示从起点出发并回到起点的路径。
（其实与best_points差别就是在best_points后加入起点（best_points的第一个点））

fig, ax = plt.subplots(1, 2)
best_points_ = np.concatenate([best_points, [best_points[0]]])
best_points_coordinate = points_coordinate[best_points_, :]
ax[0].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], 'o-r')
ax[1].plot(ga_tsp.generation_best_Y)
plt.show()

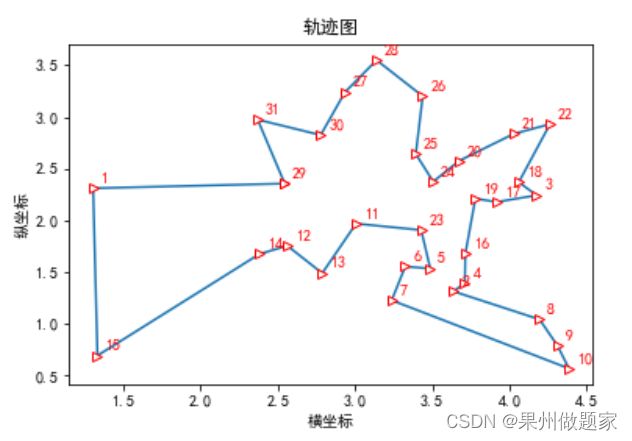
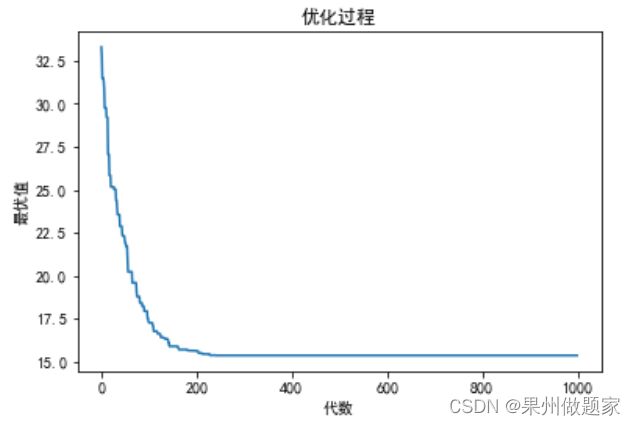
四、求解结果

城市序列与距离：

TSP图和Loss图：

五、完整源代码

python源码：

#遗传算法求解31座城市的TSP问题完整代码：
import numpy as np
from scipy import spatial
import matplotlib.pyplot as plt
from sko.GA import GA_TSP
from time import perf_counter

def cal_total_distance(routine):
    '''计算总距离：输入路线,返回总距离.
    cal_total_distance(np.arange(num_points))
    '''
    num_points, = routine.shape
    return sum([distance_matrix[routine[i % num_points], routine[(i + 1) % num_points]] for i in range(num_points)])

def print_route(best_points):
    result_cur_best=[]
    for i in best_points:
        result_cur_best+=[i]
    for i in range(len(result_cur_best)):
        result_cur_best[i] += 1
    result_path = result_cur_best
    result_path.append(result_path[0])
    return result_path

if __name__=="__main__":
    file_name = 'data.csv'    #31座城市坐标数据文件
    points_coordinate = np.loadtxt(file_name, delimiter=',')
    num_points = points_coordinate.shape[0]
    distance_matrix = spatial.distance.cdist(points_coordinate, points_coordinate, metric='euclidean')
    
    start=perf_counter()       #计时开始
    # 执行遗传(GA)算法
    ga_tsp = GA_TSP(func=cal_total_distance, n_dim=num_points, size_pop=300, max_iter=1000, prob_mut=1)   #调用工具箱
    
     # 结果输出
    best_points, best_distance = ga_tsp.run()
    print("运行时间是: {:.5f}s".format(perf_counter()-start))   #计时结束
    print("最优路线：", print_route(best_points))
    print("最优值：", best_distance[0])

    best_points_ = np.concatenate([best_points, [best_points[0]]])
    best_points_coordinate = points_coordinate[best_points_, :]

    #绘图
    plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置中文显示
    plt.rcParams['axes.unicode_minus'] = False

    fig1, ax1 = plt.subplots(1, 1)
    ax1.set_title('轨迹图', loc='center')
    line=ax1.plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], marker='>', mec='r', mfc='w')
    for i in range(num_points):
        plt.text(best_points_coordinate[:, 0][i] + 0.05, best_points_coordinate[:, 1][i] + 0.05, str(best_points[i]+1), color='red')
    ax1.set_xlabel("横坐标")
    ax1.set_ylabel("纵坐标")

    fig2, ax2 = plt.subplots(1, 1)
    ax2.set_title('优化过程', loc='center')
    ax2.plot(ga_tsp.generation_best_Y)
    ax2.set_xlabel("代数")
    ax2.set_ylabel("最优值")
    plt.show()