【Deep Learning 1】GA遗传算法

本文以一个案例题目出发，详细描述了遗传算法过程，并做了两个实验复现题目

实验一：纯手打原生代码复现案例

实验二：使用第三方库scikit-opt复现案例

一、Introduction

遗传算法源自自然界生物的遗传和进化过程：通过染色体之间的选择、交叉和变异来形成。同时符合自然界优胜劣汰的规则。因此遗传算法本质上是一种全局优化搜索算法，即已知评价方程和参数范围，求解目标函数最优解。

二、 Principle

2.1 算法总体流程

算法流程

1 设计编码器和解码器

2 初始化种群 

3 个体适应度评价

4 交叉运算

5 变异运算

6 选择运算

7 判断遗传进化是否达到迭代阈值

接下来我们使用GA来解决以下问题

 题目：求解以下函数的最小值

题目分析：我们目标是求解该函数的最小值。限制条件为x的取值范围在-20~20

2.2 编码器和解码器

GA最先要做的事情就是对自变量X编码成字符串，每个字符类似于生物学中的染色体，而一条字符串就是一个个体。该题目中变量x整数为20-（-20）=40个。很多时候我们变量是有精度，因此我们需要对其进行扩充，如40*10=400个。

接下来我们要考虑使用什么规则来对X进行编码，最常见的方法是使用0、1构成的二进制编码

因此我们采用9位二进制数表示x值。

代码上我们设计Encoder编码器函数和Decoder解码器函数进行编码和解码。

2.2 初始化种群

初始化种群主要是随机产生几个个体。假设我们随机产生了4个个体

个体编码	数值	染色体
1号	11.7	100111101
2号	-11.6	001010100
3号	-6.9	010000011
4号	6.2	100000110

2.3 个体适应度评价

衡量一条染色体质量的指标即适应度，通常来说就是将个体代入目标函数的函数值

个体编码	数值	染色体	f(x)
1号	11.7	100111101	273.78
2号	-11.6	001010100	269.12
3号	-6.9	010000011	95.22
4号	6.2	100000110	76.88

2.4 交叉

染色体在进化的过程中会不断进行两两交叉配对。染色体具体交叉配对的过程为从几号位置染色体交换染色体

个体编码	染色体	f(x)	交换个体编码对象	交换位置
1号	100111101	273.78	3号	5
2号	001010100	269.12	4号	4
3号	010000011	95.22	1号	8
4号	100000110	76.88	2号	8

交换后的结果为

个体编码	染色体	f(x)
1号	100110011	228.97
2号	001000110	338.0
3号	010000011	95.22
4号	100000110	76.88

2.5 变异

看过《异形》的小伙伴都知道生物可能会发生变异。而变异的具体过程就是染色体发生突变。本例子中我们需要设定一个变异概率的值，某条染色体0、1互换。若变异后的超出变量x的阈值，则变异失败

个体编码	染色体	是否发生变异	变异位置	是否成功变异	变异结果
1号	100110011	是	3	是	100010011
2号	001000110	否	-	-	-
3号	010000011	否	-	-	-
4号	100000110	否	-	-	-

2.6 选择

在自然界中有着优胜劣汰的规则，因此我们需要挑选出适应度高的个体。在自然界中，有着良好基因的个体往往有更大概率存活下来，根据该规律，传统的使用的是轮盘赌算法，即适应度与被选择的概率成正比，适应度越高，被选择的概论也就越高。

但是因为所求的是最小值，即函数值越高，概率越低，因此需要特别设计一个规则。

作者想出了两种方案

第一种方案，是从适应度函数下手如下，那么求解最小值等价于求解该适应度函数的最大值，这样可以继续使用传统的轮盘赌算法 

第二种方案，是从轮盘赌算法下手，f(x)概率越小，分子越小,f(x0值越小，种群适应度越高。且概率之和为1，下述的代码也是采用本方案。这里的n是初始化种群的个体数量

注意这里被选中次数之和与选中前的个数总和一致

个体编码	数值	染色体	f(x)	被选择的概率	被选中的次数
1	7.5	100010011	112.5	0.2056	1
2	-13.0	001000110	338.0	0.2078	-
3	-6.9	010000011	95.22	0.2889	1
4	6.2	100000110	76.88	0.2974	2

选择之后进行繁衍，更新表格数据为

个体编码	染色体	f(x)	初始f(x)（这里做对比）
1	100010011	112.5	273.78
2	010000011	95.22	269.12
3	100000110	76.88	95.22
4	100000110	76.88	76.88

可以看到经过一轮的遗传进化之后，种群的f(x)普遍降低，种群的适应度总体提高不少

最后判断是否达到最大迭代次数，若没有，则重新回到2.3 步骤

三、Experiment

3.1 方案一：原生代码

Code

import numpy as np
from matplotlib import pyplot as plt

PRECISION = 10.0  # 自变量精度
INDIVIDUALS_NUM = 50  # 初始化个体数量
EVOLUTION_NUM = 10000  # 进化次数
LOWER_LIMIT = -20  # 染色体下限值
UPPER_LIMIT = 20  # 染色体上限值
CROSS_RATE = 0.6  # 交叉概率
MUTATION_RATE = 0.005  # 变异概率


def encoder(x):
    result = []
    for i in x:
        i = bin(int((i + 20) * PRECISION))[2:]
        for j in range(9 - len(i)):
            i = '0' + i
        result.append(i)
    return result


def decoder(x):
    result = []
    for i in x:
        i = int(i, 2) - 200
        i = i / PRECISION
        result.append(i)
    return result


def initialize():
    def transform(x):
        return (x - 200) / PRECISION

    p = np.random.randint(0, 400, size=INDIVIDUALS_NUM)
    p = encoder(list(map(transform, p)))
    return p


def choose(x, ada):
    x, ada = np.asarray(x), np.asarray(ada)
    #print('概率情况',(1-ada / ada.sum())/(INDIVIDUALS_NUM-1))
    index = np.random.choice(np.arange(INDIVIDUALS_NUM), size=INDIVIDUALS_NUM, replace=True, p=(1-ada / ada.sum())/(INDIVIDUALS_NUM-1))
    #print('\nChoose index:', index)
    return x[index]


def threshold_limit(x):
    l = []
    l.append(x)
    x = decoder(l)[0]
    if x >= -20 and x <= 20:
        return True
    else:
        return False


def cross(x):
    result = []
    for chromosome in x:
        chromosome_A = list(chromosome)
        if np.random.rand() < CROSS_RATE:
            chromosome_B = x[np.random.randint(INDIVIDUALS_NUM)]
            cross_points = np.random.randint(low=0, high=8)
            # 观察交叉后的数据会不会超过自变量x的阈值
            fake = chromosome_A
            fake[cross_points:] = list(chromosome_B)[cross_points:]
            if threshold_limit(''.join(fake)):
                chromosome_A = fake
        result.append(''.join(chromosome_A))
    return result


def mutations(x):
    result = []
    for chromosome in x:
        if np.random.rand() < MUTATION_RATE:
            mut_points = np.random.randint(0, 8)
            chromosome = list(chromosome)
            # 观察变异后的数据会不会超过自变量x的阈值
            fake = chromosome
            fake[mut_points] = '1' if chromosome[mut_points] == '0' else '0'
            if threshold_limit(''.join(fake)):
                chromosome = fake
        result.append(''.join(chromosome))
    return result


def adaptability(list):
    result = []
    for i in list:
        result.append(2 * pow(i, 2))
    return result


def best_chr(x):
    dec = decoder(x)
    ada = adaptability(dec)
    best_index = np.argmin(ada)
    return (ada[best_index])


if __name__ == '__main__':
    # 初始化种群
    pop = initialize()
    #print(decoder(pop))
    print('Initializing Populations', pop)
    best=[]
    for i in range(EVOLUTION_NUM):
        ada = adaptability(decoder(pop))
        #print('Adaptability', ada)
        pop = cross(pop)
        #print('Cross', pop)
        pop = mutations(pop)
        #print('Chromosome',pop)
        #print('hanshuzhi',decoder(pop))
        pop = choose(pop, ada)
        #print('Choose', pop)
        best.append(best_chr(pop))

    plt.plot(range(EVOLUTION_NUM), best)
    plt.ylabel('f(x)')
    plt.xlabel('Epoch')
    plt.show()

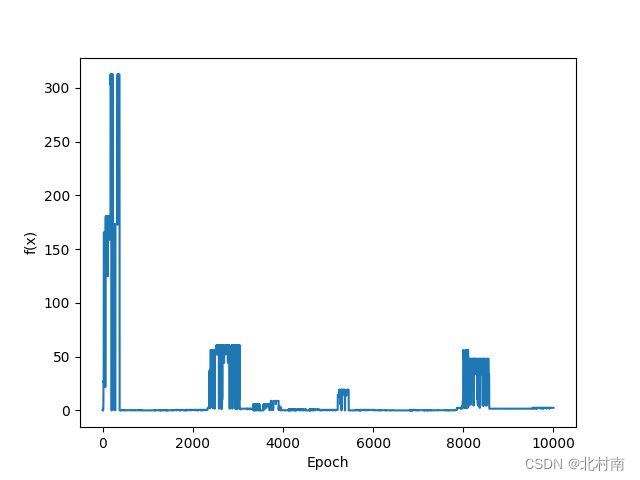
Result

这个结果非常有意思

1 目标函数值最优解为0,所求的结果大部分接近0，且最终也趋向于0，说明该算法是有效的

2 中间有几个凸集，主要是因为有染色体变异的情况，但最终还是趋向于0了

3 这其实反映了生物进化的过程，有些时候发生了生物变异，它具有很强的适应性，在某个时期具有一定的地位。但是随着生物的不断遗传进化，物竞天择的自然规律，最终，最适应的染色体始终占据了主导地位

3.2 方案二：第三方库

安装第三方库

pip install scikit-opt

Code

from sko.GA import GA

def adapt(x):
    return 2 * pow(x, 2)

# func 适应度函数
# n_dim 自变量的个数
# size_pop 种群初始化个体数量
# max_iter 进化迭代次数
# prob_mut 变异概率
# lb 自变量下限
# ub 自变量上限
# precision 精度
ga = GA(func=adapt, n_dim=1, size_pop=50, max_iter=800, prob_mut=0.001, lb=-20, ub=20, precision=1e-2)
best_x, best_y = ga.run()
print('best_x:', best_x, '\n', 'best_y:', best_y)