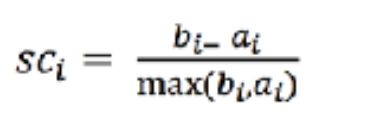k-means算法简介

k-means算法简介

一.什么是k-means

我们假设有这样一个场景。有一大堆硬币毫无任何规则的散落在那里，你事先并不知道这些硬币都是哪个国家的硬币。但是你却想按照国家对这些硬币进行分门别类。该怎么办？

这个时候就需要k-means算法的支持。回到上述例子，我们首先事先并不知道有哪些类别的硬币，即：并不知道目标值是什么，所以k-means算法是一种无监督的学习方式。同时，把不同国家队硬币分门别类，故，这是一种分类算法。“物以类聚，币以国分”，所以k-means这种算法又是“聚类”算法的一种。

二.k-means算法的步骤

k-means算法有如下步骤：

• step1、随机设置K个特征空间内的点作为初始的聚类中心点。说到这里，应该能想到：这个K是一个超参数，需要自己指定。如果不好拿捏，那么可以运用交叉验证和网格搜索的方式进行处理。

• step2、对于其他每个点，分别计算到它们到K个中心的距离（即：每个点都要经过k次计算），每个点经过k次计算之后，在这k个计算结果当中选择最近的一个聚类中心点作为标记类别

• step3、接着对着标记的聚类中心之后，重新计算出每个聚类的新中心点（平均值），并且与旧的中心点作比较

• step4、如果计算得出的新中心点与原中心点一样，那么结束，否则重新进行第二步过程

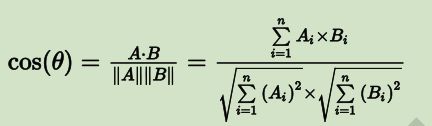
在step2当中，提到了一个名词：中心距离。那么K-means算法当中的这个中心距离是怎么衡量的呢？

与k-近邻算法一样，可以是欧氏距离，可以是曼哈顿距离，也可以是余弦距离。这个也被称为相似度算法，对于这个，不止这三个，具体看：聚类算法第一部分

其中，A，B代表属性向量。

三.k-means性能评估指标

k-means属于聚类算法的一种，关于聚类算法的评估指标，有不止一种方式，这里，只简单的介绍一些轮廓系数，它的公式如下：

其他的评估指标，具体见：聚类算法第四部分
对于每个点i为聚类数据中的样本 ，bi 为i 到其它族群的所有样本的距离的最小值，ai为i 到本身簇的距离平均值

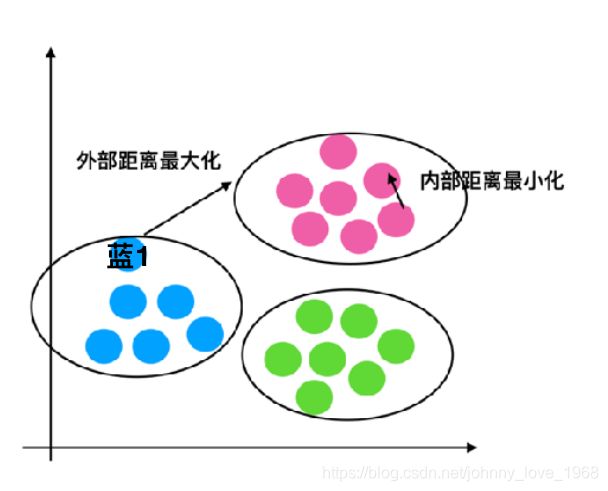
最终计算出所有的样本点的轮廓系数平均值。这个值越接近1，说明性能越好，越接近-1，则说明性能越差。k-means所要达到的最终的目的：外部距离（即：不同类别之间的距离）要尽可能的大，但是内部距离（即：相同类别的点之间的距离）要尽可能的小，如下图所示：

在sklearn中，为我们提供了k-means性能评估指标的API如下：

sklearn.metrics.silhouette_score

sklearn.metrics.silhouette_score(X, labels) #计算所有样本的平均轮廓系数
"""
X：特征值
labels：被聚类标记的目标值
"""

四.k-means的使用

4.1 相关API

sklearn中k-means的api如下：

sklearn.cluster.KMeans

sklearn.cluster.KMeans(n_clusters=8,init=‘k-means++’) #k-means聚类
"""
n_clusters:开始的聚类中心数量
init:初始化方法，默认为'k-means ++’
labels_:默认标记的类型，可以和真实值比较（不是值比较）
"""

4.2 具体案例

有几个表格，记录了一个商场客户买东西的情况，根据所买东西类别，判断用户类型

import pandas as pd
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_score

# 读取四张表的数据
prior = pd.read_csv("./Data/Instacart/order_products__prior.csv")
products = pd.read_csv("./Data/Instacart/products.csv")
orders = pd.read_csv("./Data/Instacart/orders.csv")
aisles = pd.read_csv("./Data/Instacart/aisles.csv")

# 将四张表合并成一个表
_mg = pd.merge(prior,products,on = ['product_id','product_id'])
_mg = pd.merge(_mg,orders, on = ['order_id','order_id'])
mt = pd.merge(_mg,aisles,on = ['aisle_id','aisle_id'])

#交叉表
#将user_id作为列，aisle作为行，形成了一个二维表,这样就把每个用户都买了什么类别的商品展示出来了
cross = pd.crosstab(mt['user_id'],mt['aisle'])

# 主成分分析，先进行降维处理
pca = PCA(n_components=0.9)
data = pca.fit_transform(cross)
# 减少样本数量
x = data[:500]

# k-means算法，将数据分成四个类别
km = KMeans(n_clusters=4)
km.fit(x)
#预测
predict = km.predict(x) #predict为一个np二维数组，元素值相同的为一类

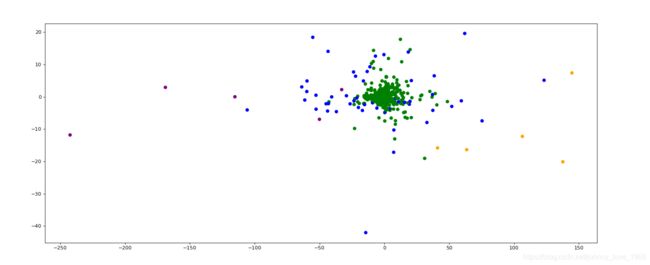
# 画图
plt.figure(figsize=(20,8),dpi = 80)

# 四个类别分别用四个颜色表示
colors = ['orange','green','blue','purple']
colr = [colors[i] for i in predict]
plt.scatter(x[:,1],x[:,20],color = colr)

plt.show()

# 评估聚类效果，计算轮廓系数
silhouette_score(x, predict)

输出结果如下：