【论文笔记】DSCN:基于深度孪生神经网络的光学航空图像变化检测模型
本文是论文《Change Detection Based on Deep Siamese Convolutional Network for Optical Aerial Images》的阅读笔记。
一、相关工作
根据网络的结构,现在变化检测的模型主要有三类,一是基于孪生神经网络的,二是基于伪孪生神经网络的,三是基于两通道的,孪生神经网络的两个分支是共享参数的,而伪孪生神经网络的两个分支是不共享参数的,两通道的是先把图像在通道维度concatenate起来,然后进行处理。在特征提取任务中,孪生神经网络更好有更好的解释性,因为两个分支共享参数,这意味着它们使用相同的方法从两张图像中提取特征,而由于变化检测中的两张图像是同源、具有相同属性的,所以通过相同方式提取特征更为自然。
二、方法和网络结构
文章贡献有:使用孪生神经网络来提取特征,使用加权对比损失来减少样本的不平衡,即不仅未变化的像素,而且变化的像素也被充分考虑到目标函数中。加权对比损失的优点是变化像素对的特征向量会远离彼此,而未变化像素对的特征向量会靠近彼此。
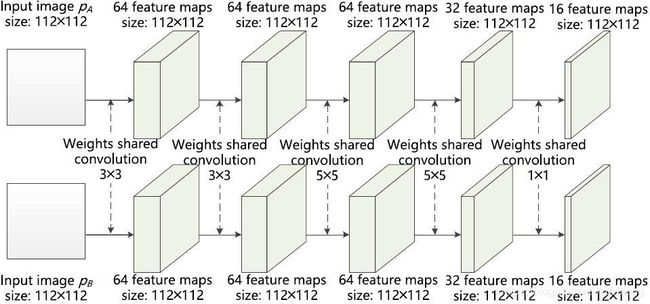
设计的孪生神经网络的具体结构如上。
1. 标记
-
X X X:输入图像
-
x ( i , j ) x(i,j) x(i,j):输入图像在 ( i , j ) (i,j) (i,j)位置处的灰度值向量
-
G w ( X ) G_w(X) Gw(X):输出特征向量
-
D w ( X 1 , X 2 ) D_w(X_1,X_2) Dw(X1,X2):两张输入图像之间的距离图
-
D w ( X 1 , X 2 ) i , j D_w(X_1,X_2)_{i,j} Dw(X1,X2)i,j:像素 x 1 ( i , j ) x_1(i,j) x1(i,j)和 x 2 ( i , j ) x_2(i,j) x2(i,j)之间参数化的距离函数(欧氏距离),简写为 D i , j D_{i,j} Di,j,其公式如下:
D w ( X 1 , X 2 ) i , j = ∥ G w ( X 1 ) i , j − G w ( X 2 ) i , j ∥ 2 D_{w}\left(X_{1}, X_{2}\right)_{i, j}=\left\|G_{w}\left(X_{1}\right)_{i, j}-G_{w}\left(X_{2}\right)_{i, j}\right\|_{2} Dw(X1,X2)i,j=∥∥∥Gw(X1)i,j−Gw(X2)i,j∥∥∥2 -
Y Y Y:二值GT图, y ( i , j ) = 0 y(i,j)=0 y(i,j)=0表示相关图像对未变化, y ( i , j ) = 1 y(i,j)=1 y(i,j)=1表示变化
-
( Y , X 1 , X 2 ) k (Y,X_1,X_2)^k (Y,X1,X2)k:第 k k k个标记的训练样本对
-
L U , L C L_U,L_C LU,LC:分别表示为未变化像素对和变化像素对的损失函数
-
P P P:训练样本对的个数
-
m m m:margin,边际
2. 损失函数
损失函数定义如下:
ℓ ( W ) = ∑ k = 1 P L ( W , ( Y , X 1 , X 2 ) k ) = ∑ k = 1 P ∑ i , j ( 1 − y i , j k ) L U ( D i , j k ) + y i , j k L C ( D i , j k ) \begin{aligned}\ell(W) &=\sum_{k=1}^{P} L\left(W,\left(Y, X_{1}, X_{2}\right)^{k}\right) \\&=\sum_{k=1}^{P} \sum_{i, j}\left(1-y_{i, j}^{k}\right) L_{U}\left(D_{i, j}^{k}\right)+y_{i, j}^{k} L_{C}\left(D_{i, j}^{k}\right)\end{aligned} ℓ(W)=k=1∑PL(W,(Y,X1,X2)k)=k=1∑Pi,j∑(1−yi,jk)LU(Di,jk)+yi,jkLC(Di,jk)
L U , L C L_U,L_C LU,LC定义如下:
L U ( D i , j k ) = 1 2 ( D i , j k ) 2 L C ( D i , j k ) = 1 2 { max ( 0 , m − D i , j k ) 2 } \begin{aligned}L_{U}\left(D_{i, j}^{k}\right) &=\frac{1}{2}\left(D_{i, j}^{k}\right)^{2} \\L_{C}\left(D_{i, j}^{k}\right) &=\frac{1}{2}\left\{\max \left(0, m-D_{i, j}^{k}\right)^{2}\right\}\end{aligned} LU(Di,jk)LC(Di,jk)=21(Di,jk)2=21{max(0,m−Di,jk)2}
对变化检测来说,变化像素对和未变化像素对的个数变化非常大,所以需要根据实际情况对损失函数进行加权,所以最终的损失函数如下:
L ( W , ( Y , X 1 , X 2 ) k ) = ∑ i , j ( 1 − y i , j k ) 1 2 ( D i , j k ) 2 w U + y i , j k 1 2 { max ( 0 , m − D i , j k ) 2 } w C \begin{aligned}L\left(W,\left(Y, X_{1}, X_{2}\right)^{k}\right)=& \sum_{i, j}\left(1-y_{i, j}^{k}\right) \frac{1}{2}\left(D_{i, j}^{k}\right)^{2} w_{U} \\&+y_{i, j}^{k} \frac{1}{2}\left\{\max \left(0, m-D_{i, j}^{k}\right)^{2}\right\} w_{C}\end{aligned} L(W,(Y,X1,X2)k)=i,j∑(1−yi,jk)21(Di,jk)2wU+yi,jk21{max(0,m−Di,jk)2}wC
其中, w U , w C w_U,w_C wU,wC是权重系数,使用平均频率平衡,其公式如下:
w U = f avg f U w C = f avg f C \begin{array}{l}w_{U}=\frac{f_{\text {avg }}}{f_{U}} \\w_{C}=\frac{f_{\text {avg }}}{f_{C}}\end{array} wU=fUfavg wC=fCfavg
其中, f U , f C f_U,f_C fU,fC是未变化和变化的像素对的频率, f a v g f_{avg} favg是平均类频率,实际上平均类频率为0.5,因为只有未变化和变化两类。
上图是不加权损失、加权损失、有KNN的加权损失的对比。
3、处理流程
网络的整体模型如上。
整个模型的处理流程如下:
- 使用直方图匹配进行辐射校正
- 图像 X 1 , X 2 X_1,X_2 X1,X2被输入到孪生神经网络中,然后产生两个特征向量 G w ( X 1 ) , G w ( X 2 ) G_w(X_1),G_w(X_2) Gw(X1),Gw(X2),记为 F 1 , F 2 F_1,F_2 F1,F2
- 根据公式获得距离图 D w ( X 1 , X 2 ) D_w(X_1,X_2) Dw(X1,X2),记为 D D D,其中值越大相关像素对改变的可能性越大
- 初试变化图 T T T同简单的阈值分割法获得
- 使用KNN算法对 T T T进行提升,得到最终的变化图 M M M
三、实验
使用的数据集是SZTAKI AirChange Benchmark Set数据集,其包括三个已经配准的光学航空图像数据集:SZADA, TISZADOB和ARCHIEVE,其中SZADA 和TISZADOB被用作训练和测试。使用的baseline为CXM和SCCN,使用的评价指标有正确率Pr、召回率Rc和F值Fr。
不同方法在两个数据集上的结果对比。
a~f分别是两张输入图像、GT、CXM的结果、SCCN的结果、DSCN的结果。