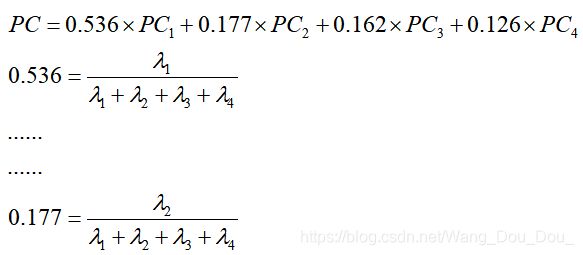数学建模——PCA主成分分析【工具:matlab】【全文7000字】
文章目录
- 一、主成分分析是什么?
- 二、主成分分析有什么用?
- 三、主成分分析的适用范围?
- 四、主成分分析怎么用?
-
- PCA的matlab代码
- 五、PCA运行结果
- 六、总结:
- 七、参考附录:
笔者尽量用很通俗的语言来描述。
数学建模系列文章——总结篇:《数模美一国一退役选手的经验分享[2021纪念版]》.
一、主成分分析是什么?
主成分分析(Principal Component Analysis,PCA), 是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。
在实际项目中,为了全面分析问题,往往提出很多与此有关的变量(或因素),因为每个变量都在不同程度上反映这个课题的某些信息。而主成分分析就是把原来多个变量划为少数几个综合指标的一种统计分析方法。
二、主成分分析有什么用?
PCA,就是为了在尽量保证 “信息量不丢失”的情况下,对原始数据特征进行 降维 ,也就是尽可能将原始特征往具有最大投影信息量的维度上进行投影。将原特征投影到这些维度上,使降维后信息量损失最小。
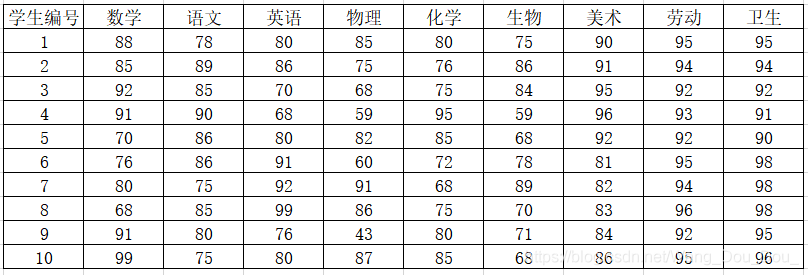
举一个简单的栗子,在某一个学校,它有一张综合信息表(10个同学,100分制)如下。
假如某位校外领导来视察 该校的学生情况,但因为下面的数据太多了,不好分析。
然后领导来请教你一个问题,能否只用两三个 “特征” 指标就能区分不同学生之间的 “差异” 。(不妨花费5秒看一看)
显然,我们可以把每位同学的总分加起来进行一个排名。但是我们并不是要去“排名”,不是用“数学、语文、英文、…” 等指标来评价学生,而是用 一种 “新” 的指标形式来评价学生。 至于这个 “新” 的指标如何产生,听我在快快说。
比如上述学生成绩中,他们有“数学、语文、英语、物理、…、卫生” 一共9个 “特征” 。那我们现在可以用这9个 “特征” 来 “区分” 这10个学生。
那试想,我们能否用更少的 “特征” 就能来 “区分” 这10个学生的 “差异” 呢?常规的想法是,删除一些 “特征” 指标,比如删去 “劳动” 和 “卫生” 这两个指标。用剩下的8个 “特征” 来 区分。
那为什么不删去 “数学” 或者 “英语” 这样的 “特征” 指标呢? 因为我们觉得这两科目里包含的 信息量 更大! 为什么说 信息量更大 呢?因为 在 “数学” 或者 “英语” 这样的 “特征” 指标中,10位同学之间的 分差 比较大,更容易用这样的 “特征” 来 “量化” 他们 的差别,所以说 “数学、英语” 两个 “特征” 指标包含的 信息量 更大。【其实 这里有个 最大方差理论 ,我用 分差 来解释 只是为了通俗易懂,如要详细了解PCA原理,详见 参考附录②】
而回到刚才所说的,我们为什么觉得可以删去 “劳动” 和 “卫生” 这两个“特征” 指标呢?
因为啊,在 “劳动” 和 “卫生” 这两个“特征” 指标中,10位同学之间的 分差 比较小,不容易用这样的 “特征” 来 “量化” 他们 的差别,所以 “数学、英语” 两个 “特征” 指标包含的 信息量 比较少。 所以可以删去 。
但是呢,删 “劳动” 和 “卫生” 这两个 “特征” 指标只是我们人为 用眼睛 去 “分析” 的。而如果 要用到数学的 “分析” 方法,就要用 主成分分析 了,从而提取出学生们 9个 “特征” 相互组合而成 的 “主成分(Principal Component)”【简称 PC 】 。
为什么我这里要说 “相互组合而成” 的呢?【敲黑板,重点来了】
现在 假设 我已经 对这张成绩表做了 主成分分析。然后 假设 得到了下面的结果,然后我来解释一下。【我随便写的结果哈,不一定正确,只是为了用来说明知识点】
①PC1 即是 第一 主成分,它由 x1、x2、…、x9 线性组合而成。同理,PC2 2是 第二 主成分,也是由 x1、x2、…、x9 线性组合而成。以此类推。
②为什么 PC1 是 第一 呢?,因为它所对应的 λ 最大,λ 是 特征值,大家先留个概念。 特征值越大,说明该 主成分 越重要。
③贡献率,值得是 这个主成分 对保留 “信息量” 的贡献力量。越大越好。 它的计算公式在后续讲。
④ “x1” 即是 “数学” 这一 “特征” 指标, 同理 “x2” 是 “语文” 这一 “特征” 指标,…,而 “x9” 即是 “卫生” 这一 “特征” 指标。
⑤至于 x 前面的那个系数,就是通过 主成分分析 的得到的结果( 特征向量 ),可以从 PC9 那里看到它们之间的关系。至于特征向量,它是 主成分分析 计算得到的结果,后续再解释。
那么,刚刚我说的 “相互组合而成” 的意思就是:这里的 9个PC ,也就是 9个主成分,每个 PC 都是由 9个 “特征” 与 权值系数 [即 特征向量] 相乘后 再相加 组合而成的。**
那这样看似好像 还没有解决我们想要解决的问题诶…因为对于我们得到的每个主成分 PCi,它都还是需要 9个 “特征” 指标来计算。
但是,我们有了 贡献率 过后,如果我们觉得,只要能达到 90% 的累计贡献率就可以的话,那我们就只用选出前3个PCi 就可以了。因为61.55%+20.13%+11.98% > 90% 。那么 就可以写出下面的表达式:【两种都可以,但第二种更佳】
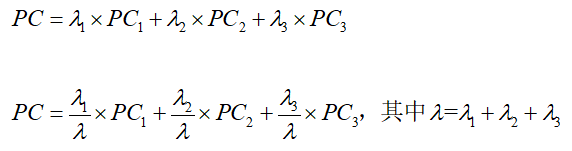
这里的PC就是,最终的综合评价值的表达式。也就是说,我们只用前三个 PCi ,就能够在 保留 较大信息量(>90%) 的情况下,来 “区分” 这10位学生的 “差异”。
这样就从原来的 9维 降到了现在的 3维。因为原先有9个 “特征”指标,所以要在 9 个维度上去 “区分” 学生之间的 “差异”。而现在只需要 PC1、PC2、PC3 , 即可在 3 个维度上来 “区分”。 就能画如下图类似的坐标系了!

那我们就可以回答 最开始 那位 校外领导 提出的问题了!!
三、主成分分析的适用范围?
当样本的 特征属性 太多,而又需要提取较少的 综合特征 时,即可用上。
对于这里的 综合特征,就是前面说的 各 “特征” “相互组合而成” 的东西。
四、主成分分析怎么用?
用matlab,还是python,都是可以的,在这里我用的matlab。
直接上代码~步骤都在代码中
PCA的matlab代码
clear;clc
x = xlsread('主成分分析_学生成绩样例.xlsx',1,'E5:M14') % 读数据
[n,p] = size(x); % n是样本个数,p是指标个数
% n返回的是行数,p返回的是列数
% 第一步:数据x标准化
X=zscore(x); % zscore():matlab内置的标准化函数(x-mean(x))/std(x)
% 第二步:计算样本协方差矩阵
C = cov(X);
% 其实以上两步可合并为下面的一步:直接计算样本相关系数矩阵
C = corrcoef(x);
disp('样本相关系数矩阵为:')
disp(C);
% 第三步:计算C的特征值和特征向量
% 注意:C是半正定矩阵,所以其特征值不为负数
% C同时是对称矩阵,Matlab在处理对称矩阵时,会将特征值按照从小到大排列
[V,D] = eig(C); % eig():计算特征值和特征向量
% V 特征向量矩阵 D是由特征值构成的对角矩阵
% 第四步:计算主成分贡献率和累计贡献率
lambda = diag(D); % diag():用于得到一个矩阵的主对角线元素值(返回的是列向量)
lambda = lambda(end:-1:1); % 因为lambda向量是从小大到排序的,我们将其调个顺序
contribution_rate = lambda / sum(lambda); % 计算贡献率
cum_contribution_rate = cumsum(lambda)/ sum(lambda); % 计算累计贡献率 cumsum():求累加值的函数
disp('特征值为:')
disp(lambda')
disp('贡献率为:')
disp(contribution_rate')
disp('累计贡献率为:')
disp(cum_contribution_rate')
disp('与特征值对应的特征向量矩阵为:') % 注意:这里的特征向量要和特征值一一对应,之前特征值相当于颠倒过来了,因此特征向量的各列需要颠倒过来
V=rot90(V)'; % rot90():可以使一个矩阵逆时针旋转90度,然后再转置,就可以实现将矩阵的列颠倒的效果
disp(V)
xlswrite('主成分分析_学生成绩样例.xlsx',lambda,2); % 把特征值写入当前文件的 脚本2 里面
xlswrite('主成分分析_学生成绩样例.xlsx',V,3); % 把特征向量写入当前文件的 脚本3 里面
五、PCA运行结果
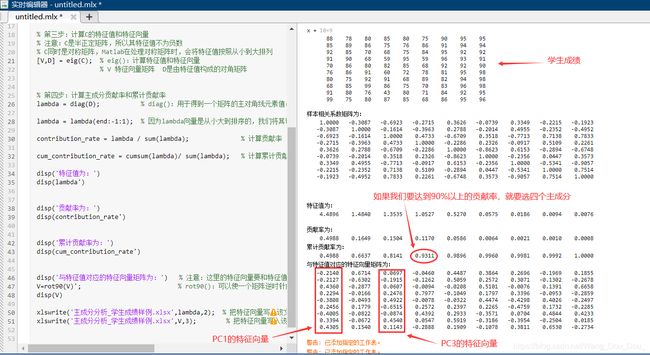
由上图的结果可知,在我们提取主成分时 ,如果想到达到 90%贡献率 的预期的话,我们得选出前4个主成分,即 PC1、PC2、PC3 、PC4,它们的表达式如下图所示。
而 综合评价值的表达式 则如下:
六、总结:
通过上述一系列的操作,我们就可以给那位 校外领导 呈现一张 有4个 主成分(PC1、PC2、PC3 、PC4) 的成绩单即可,就不用呈现给他有9个 “特征” 的成绩单了。
也就是说,我们只用前4个 PCi ,就能够在 保留 较大信息量(>90%) 的情况下,来 “区分” 这10位学生的 “差异”。
这样就从原来的 9维 降到了现在的 4维。因为原先有9个 “特征”指标,所以要在 9 个维度上去 “区分” 学生之间的 “差异”。而现在只需要 PC1、PC2、PC3 、PC4, 即可在 4 个维度上来 “区分”。
最后,我没有详细地阐述其原理,只阐述了有什么用、怎么用。如要了解详细的原理,可以看看文章最后的参考附录吧。
七、参考附录:
[1] 《傻瓜攻略(一)——MATLAB主成分分析(PCA)代码及结果分析实例》
链接: https://blog.csdn.net/qq_36108664/article/details/104972122.
[2] 《PCA:详细解释主成分分析》:通过这篇文章,你可以比较系统地学习到:PCA的原理】
链接: https://blog.csdn.net/lanyuelvyun/article/details/82384179.
[3] 《数学建模——主成分分析(SPSS)》:通过这篇文章,你可以学习到:如何用SPSS处理PCA】
链接: https://zhuanlan.zhihu.com/p/63139206.
[4] 《【中字】主成分分析法(PCA)| 分步步骤解析 看完你就懂了!》:看完这个视频,你可以 更直观地 学习PCA】
链接: https://zhuanlan.zhihu.com/p/63139206.
数学建模系列文章——总结篇:《数模美一国一退役选手的经验分享[2021纪念版]》.
⭐️ ⭐️