目标检测中常用的损失函数汇总

目标检测

目标检测中的损失函数通常由两部分组成：classification loss 和 bounding box regression loss。

类别损失

交叉熵

Softmax+交叉熵
对于二分类而言，交叉熵损失函数形式如下：

交叉熵损失函数通过不断缩小两个分布的差异，使预测结果更可靠。
之后谷歌在交叉熵的基础上提出了Label Smoothing（标签平滑），解决over-confidence的问题。
对于像交叉熵这样的loss，一旦output有些偏差，loss值就往无穷大方向走，就逼迫模型去接近真实的label值。接近label值之后，如果这个训练数据是错误标记的或者训练数据并不能完全覆盖所有类型，就会出现过拟合现象。所以适当调整label，让两端的极值往中间凑一凑，可以增加泛化性。
Label Smoothing其实就是将原来的label取值范围从[0,1]改为 [ε，1-ε]
参考文章：标签平滑(label smoothing)

focal loss

focal loss出于论文Focal Loss for Dense Object Detection，主要是为了解决one-stage目标检测算法中正负样本比例严重失衡的问题，降低了大量简单负样本在训练中所占的比重，可理解为是一种困难样本挖掘。focal loss是在交叉熵损失函数上修改的。具体改进：

其中γ>0(文章中取2）使得减少易分类样本的损失，更关注困难的、错分的样本。例如γ为2，对于正类样本而言，预测结果为0.95肯定是简单样本，所以（1-0.95）的γ次方就会很小，这时损失函数值就变得更小。而预测概率为0.3的样本其损失相对很大。对于负类样本而言同样，预测0.1的结果应当远比预测0.7的样本损失值要小得多。对于预测概率为0.5时，损失只减少了0.25倍，所以更加关注于这种难以区分的样本。这样减少了简单样本的影响，大量预测概率很小的样本叠加起来后的效应才可能比较有效。
此外加入平衡因子α，用来平衡正负样本本身的比例不均，文中取值为0.25，即正样本比负样本占比小，这是因为负例易分。

位置损失

L1（MAE），L2（MSE），smooth L1损失函数

利用L1，L2或者smooth L1损失函数，来对4个坐标值进行回归。smooth L1损失函数是在Fast R-CNN中提出的。三个损失函数，如下所示：

从损失函数对x的导数可知：L1损失函数对x的导数为常数，不会有梯度爆炸的问题，但其在0处不可导，在较小损失值时，得到的梯度也相对较大，可能造成模型震荡不利于收敛。L2损失函数处处可导，但由于采用平方运算，当预测值和真实值的差值大于1时，会放大误差。尤其当函数的输入值距离中心值较远的时候，使用梯度下降法求解的时候梯度很大，可能造成梯度爆炸。同时当有多个离群点时，这些点可能占据Loss的主要部分，需要牺牲很多有效的样本去补偿它，所以L2 loss受离群点的影响较大。smooth L1完美的避开了L1和L2损失的缺点：

• 在[-1,1]之间就是L2损失，解决L1在0处有折点
• 在[-1， 1]区间以外就是L1损失，解决离群点梯度爆炸问题
• 当预测值与真实值误差过大时，梯度值不至于过大
• 当预测值与真实值误差很小时，梯度值足够小

上述3个损失函数存在以下不足：

• 上述三个损失函数在计算bounding box regression loss时，是独立的求4个点的loss，然后相加得到最终的损失值，这种做法的前提是四个点是相互独立的，而实际上是有一定相关性的
• 实际评价检测结果好坏的指标是IoU，这两者是不等价的，多个检测框可能有相同的loss，但IoU差异很大。

IoU Loss

IoU loss是基于预测框和真实框之间的IoU（交并比）的，IoU定义如下：

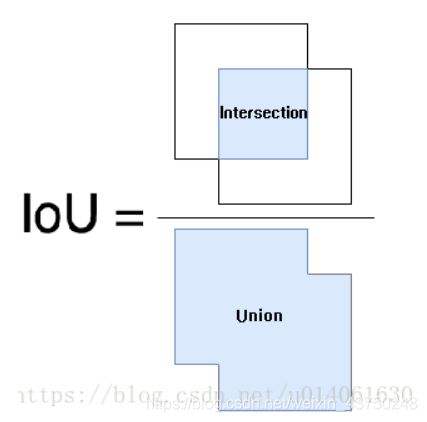
其中P代表预测框，G代表真实框。

IoU loss的定义如下：

GIoU loss

IoU反映了两个框的重叠程度，在两个框不重叠时，IoU衡等于0，此时IoU loss恒等于1。而在目标检测的边界框回归中，这显然是不合适的。因此，GIoU loss在IoU loss的基础上考虑了两个框没有重叠区域时产生的损失。具体定义如下：
其中，C表示两个框的最小包围矩形框，R(P,G)是惩罚项。从公式可以看出，当两个框没有重叠区域时，IoU为0，但R依然会产生损失。极限情况下，当两个框距离无穷远时，R→1

DIoU Loss

IoU loss和GIoU loss都只考虑了两个框的重叠程度，但在重叠程度相同的情况下，我们其实更希望两个框能挨得足够近，即框的中心要尽量靠近。因此，DIoU在IoU loss的基础上考虑了两个框的中心点距离，具体定义如下：

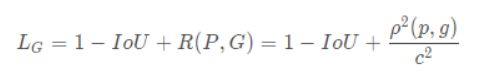
其中，ρ表示预测框和标注框中心端的距离，p和g是两个框的中心点。c表示两个框的最小包围矩形框的对角线长度。当两个框距离无限远时，中心点距离和外接矩形框对角线长度无限逼近，R→1
下图直观显示了不同情况下的IoU loss、GIoU loss和DIoU loss结果：

其中，绿色框表示标注框，红色框表示预测框，可以看出，最后一组的结果由于两个框中心点重合，检测效果要由于前面两组。IoU loss和GIoU loss的结果均为0.75，并不能区分三种情况，而DIoU loss则对三种情况做了很好的区分。

CIoU Loss

DIoU loss考虑了两个框中心点的距离，而CIoU loss在DIoU loss的基础上做了更详细的度量==，具体包括：

• 重叠面积
• 中心点距离
• 长宽比

具体定义如下：

def box_ciou(box1, box2):
	"""
	input:
		box1: shape = [batch_size, anchor_num, feat_h, feat_w, 4(xywh)] 
		box2: shape = [batch_size, anchor_num, feat_h, feat_w, 4(xywh)] 
	output:
		ciou: shepe = [batch_size, anchor_num, feat_h, feat_w, 1]
	"""
	# 计算box的左上角和右下角
	b1_xy = box1[..., :2]
	b1_wh = box1[..., 2:4]
	b1_wh_half = b1_wh / 2
	b1_mins = b1_xy - b1_wh_half
	b1_maxs = b1_xy + b1_wh_half
	
	b2_xy = box2[..., :2]
	b2_wh = box2[..., 2:4]
	b2_wh_half = b2_wh / 2
	b2_mins = b2_xy - b2_wh_half
	b2_maxs = b2_xy + b2_wh_half
	# 计算iou
	intersect_mins = torch.max(b1_mins, b2_mins)
	intersect_maxs = torch.min(b1_maxs, b2_maxs)
	intersect_wh = torch.max(intersect_maxs - intersect_mins, torch.zero_like(intersect_maxs))
	intersect_area = inersect_wh[..., 0] * intersect_area[..., 1]
	b1_area = b1_wh[..., 0] * b1_wh[..., 1]
	b2_area = b2_wh[..., 0] * b2_wh[..., 1]
	union_area = b1_area + b2_area - intersect_area
	iou = intersect_area / torch.clamp(union_area, min=1e-6)
	# 计算中心的差距
	center_distance = torch.sum(torch.pow((b1_xy - b2_xy), 2), -1)
	# 计算两个框的最小外包矩形的对角线距离
	enclose_mins = torch.min(b1_mins, b2_mins)
	enclose_maxs = torch.max(b1_maxs, b2_maxs)
	enclose_wh = torch.max(enclose_maxs - enclose_mins, torch.zeros_like(enclose_maxs))
	enclose_diagonal = torch.sum(torch.pow(enclose_wh, 2), -1)
	
	v = (4/(math.pi ** 2) * torch.pow((torch.atan((b1_wh[..., 0]/torch.clamp(b1_wh[..., 1], min=1e-6))-torch.atan(b2_wh[..., 0]/torch.clamp(b2_wh[..., 1], min=1e-6))), 2)
	alpha = v / torch.clamp((1 - iou + v), min=1e-6)
	ciou = 1 - iou + 1.0 * center_distance / torch.clamp(enclose_diagonal, min=1e-6) + alpha * v
	return ciou	

语义分割