连续时间与离散时间傅里叶变换、傅里叶变换与傅里叶级数的关系
文章目录
-
- 1. 连续时间傅里叶变换(CTFT)与离散时间傅里叶变换(DTFT)的关系
- 2. 傅里叶变换(FT)与傅里叶级数(FS)的关系
1. 连续时间傅里叶变换(CTFT)与离散时间傅里叶变换(DTFT)的关系
连续时间傅里叶变换 (C ontinuous T ime F ourier T ransform ) 和 离散时间傅里叶变换 (D iscrete T ime F ourier T ransform) 数学表达形式不同,但本质是一样的。联系两者的桥梁就是 时域冲激采样。
时域冲激信号框图:
现从的 2 个角度来计算 x ^ ( t ) \hat{x}(t) x^(t) 的 Fourier Transform:
-
利用“卷积性质”
原信号和冲激串信号的傅里叶变换为
x ( t ) ↔ F T X ( j w ) δ T ( t ) ↔ F T 2 π T ∑ k = − ∞ ∞ δ ( t − k 2 π T ) \begin{aligned} x(t) &\xleftrightarrow{\mathrm{FT}} X(jw)\\ \delta_T(t) &\xleftrightarrow{\mathrm{FT}} \frac{2\pi}{T}\sum_{k=-\infty}^{\infty} \delta(t - k\frac{2\pi}{T}) \end{aligned} x(t)δT(t)FT X(jw)FT T2πk=−∞∑∞δ(t−kT2π)
时域相乘等于频域卷积,则冲激采样信号
x ^ ( t ) = x ( t ) δ T ( t ) ↔ F T 1 2 π X ( j w ) ∗ 2 π T ∑ k = − ∞ ∞ δ ( w − 2 π T k ) = 1 T ∑ k = − ∞ ∞ X ( j w − j 2 π T k ) (1) \begin{aligned} \hat{x}(t) &= x(t) \textcolor{blue}{\delta_T(t)}\\ & \xleftrightarrow{\mathrm{FT}} \frac{1}{2\pi} X(jw) * \textcolor{blue}{\frac{2\pi}{T} \sum_{k=-\infty}^{\infty} \delta (w - \frac{2\pi}{T} k)}\\ &= \textcolor{blue}{\frac{1}{T}} \sum_{k=-\infty}^{\infty} X(jw - \textcolor{blue}{j\frac{2\pi}{T}k}) \end{aligned} \tag{1} x^(t)=x(t)δT(t)FT 2π1X(jw)∗T2πk=−∞∑∞δ(w−T2πk)=T1k=−∞∑∞X(jw−jT2πk)(1)
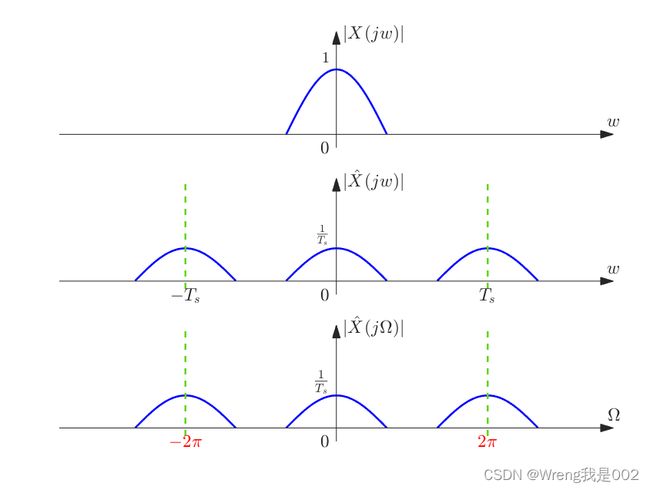
根据此式可知, x ^ ( t ) \hat{x}(t) x^(t)的频谱是原信号频谱周期延拓(幅度变小为原来的 1 / T 1/T 1/T倍),其频谱如下图所示。
-
利用 F T \mathrm{FT} FT 的定义
F T [ x ^ ( t ) ] = ∫ − ∞ ∞ x ^ ( t ) e − j w t d t = ∫ − ∞ ∞ ∑ k = − ∞ ∞ x ( k T ) δ ( t − k T ) e − j w t d t = ∑ k = − ∞ ∞ x ( k T ) ∫ − ∞ ∞ δ ( t − k T ) e − j w t d t = ∑ k = − ∞ ∞ x ( k T ) e − j w k T (2) \begin{aligned} \mathrm{FT}[\hat{x}(t)] &= \int_{-\infty}^{\infty} \hat{x}(t) e^{-jwt} dt \\ &= \int_{-\infty}^{\infty} \textcolor{blue}{\sum_{k=-\infty}^{\infty} x(kT)\delta (t-kT)} e^{-jwt} dt\\ &= \textcolor{blue}{\sum_{k=-\infty}^{\infty} x(kT)} \int_{-\infty}^{\infty} \delta(t - kT) e^{-jwt} dt\\ &= \sum_{k=-\infty}^{\infty} x(kT) e^{-jwkT} \tag{2} \end{aligned} FT[x^(t)]=∫−∞∞x^(t)e−jwtdt=∫−∞∞k=−∞∑∞x(kT)δ(t−kT)e−jwtdt=k=−∞∑∞x(kT)∫−∞∞δ(t−kT)e−jwtdt=k=−∞∑∞x(kT)e−jwkT(2)
记 x ( k T ) = x [ k ] , w T = Ω x(kT) = x[k],\textcolor{red}{wT=\Omega} x(kT)=x[k],wT=Ω,上式可化为 ∑ k = − ∞ ∞ x [ k ] e − j Ω k \textcolor{red}{\displaystyle\sum_{k=-\infty}^{\infty} x[k] e^{-j\Omega k}} k=−∞∑∞x[k]e−jΩk,这就是序列 x [ n ] x[n] x[n] 的 DTFT。
其中, T \textcolor{red}T T 是采样时间 ( s a m p l e t i m e ) (sample\ time) (sample time), w \textcolor{red}w w 是模拟频率 ( r a d / s ) \mathrm {(rad/s)} (rad/s), Ω \textcolor{red}\Omega Ω 是数字频率 ( r a d ) \mathrm {(rad)} (rad),这一步相当于将模拟角频率归一化到数字角频率 [ 0 , 2 π ] [0, 2\pi] [0,2π],换了一个 x x x 轴而 y y y 轴不变,这也解释了“ DTFT 和 CTFT 的频谱为什么如此相像”。
Ω = w T = 2 π w w s ∈ [ 0 , 2 π ] r a d \Omega = wT = 2\pi \frac{w}{w_s} \in [0, 2\pi] \mathrm{rad} Ω=wT=2πwsw∈[0,2π]rad
由式 ( 1 ) (1) (1)可以绘制出 x ^ ( t ) \hat{x}(t) x^(t)的频谱,由傅里叶变换的唯一性得式 ( 2 ) (2) (2)的频谱与式 ( 1 ) (1) (1)是一样的,这也就可以解释 DTFT 与 CTFT 频谱是相似的(横坐标存在一个缩放罢了) , DTFT 与 CTFT 本质是一致的,都是由同一个东西推导出来的,只不过两者的数学表达形式不同。
DTFT 的意义:
-
更符合实际情况。我们通常只能得到离散的数据,但是这些离散的数据仍保留原信号的完整信息 / 频谱(当然是在满足一定条件下);
-
对模拟角频率进行归一化后,可忽略“采样时间不同”的影响。
例如: 分别以采样频率 f s 1 = 1 H z , f s 2 = 2 H z f_{s1} = 1 \mathrm{Hz}, f_{s2} = 2 \mathrm{Hz} fs1=1Hz,fs2=2Hz 对同一信号进行采样,得到的序列 x 1 [ n ] , x 2 [ n ] x_1[n], x_2[n] x1[n],x2[n] 肯定不同,但它们 DTFT 的频谱是一样的。
-
DTFT 和 CTFT 本质是一致的,只是数学表达形式不同,因此(有些)连续信号的性质可推广到离散序列来。
例如:
(a). 证明 x [ n ] = 1 ↔ F T 2 π ∑ l = − ∞ ∞ δ ( Ω − 2 π l ) \displaystyle x[n] = 1 \xleftrightarrow{\mathrm{FT}} 2\pi \sum_{l=-\infty}^{\infty} \delta(\Omega - 2\pi l) x[n]=1FT 2πl=−∞∑∞δ(Ω−2πl)
x [ n ] x[n] x[n] 对应的连续时间信号是 x ( t ) = 1 x(t)=1 x(t)=1,其傅里叶变换为
x ( t ) ↔ F T 2 π δ ( w ) x(t) \xleftrightarrow{\mathrm{FT}} 2\pi \delta(w) x(t)FT 2πδ(w)
进行时域冲激串采样,采样时间为 T s T_s Ts:
x ^ ( t ) ↔ F T 2 π T s ∑ l = − ∞ ∞ δ ( w − 2 π T s l ) \hat{x}(t) \xleftrightarrow{\mathrm{FT}} \frac{2\pi}{T_s} \sum_{l=-\infty}^{\infty} \delta(\textcolor{red}w - \frac{2\pi}{T_s}l) x^(t)FT Ts2πl=−∞∑∞δ(w−Ts2πl)
令 w = Ω T s w = \frac{\Omega}{T_s} w=TsΩ:
x ^ ( t ) ↔ F T 2 π T s ∑ l = − ∞ ∞ δ ( Ω T s − 2 π T s l ) \hat{x}(t) \xleftrightarrow{\mathrm{FT}} \frac{2\pi}{T_s} \sum_{l=-\infty}^{\infty} \delta(\textcolor{red}{\frac{\Omega}{T_s}} - \frac{2\pi}{T_s}l) x^(t)FT Ts2πl=−∞∑∞δ(TsΩ−Ts2πl)
利用冲激信号的展缩特性化简:
x ^ ( t ) ↔ F T 2 π T s ∑ l = − ∞ ∞ δ ( 1 T s ( Ω − 2 π l ) ) = 2 π T s 1 1 T s ∑ l = − ∞ ∞ δ ( Ω − 2 π l ) = 2 π ∑ l = − ∞ ∞ δ ( Ω − 2 π l ) \begin{aligned} \hat{x}(t) &\xleftrightarrow{\mathrm{FT}} \frac{2\pi}{T_s} \sum_{l=-\infty}^{\infty} \delta\left(\textcolor{red}{\frac{1}{T_s}}(\Omega - 2\pi l) \right)\\ &= \frac{2\pi}{T_s} \frac{1}{\textcolor{red}{\frac{1}{T_s}}}\sum_{l=-\infty}^{\infty} \delta\left(\Omega - 2\pi l \right)\\ &= 2\pi \sum_{l=-\infty}^{\infty} \delta\left(\Omega - 2\pi l \right) \end{aligned} x^(t)FT Ts2πl=−∞∑∞δ(Ts1(Ω−2πl))=Ts2πTs11l=−∞∑∞δ(Ω−2πl)=2πl=−∞∑∞δ(Ω−2πl)
得证!注意 δ ( Ω − 2 π l ) \delta(\Omega-2\pi l) δ(Ω−2πl) 是一个冲激信号,别和采样序列 δ [ n ] \delta[n] δ[n] 混淆了。(b). 单位样本串序列 δ N [ n ] ↔ F T 2 π N ∑ l = − ∞ ∞ δ ( Ω − 2 π l ) \displaystyle \delta_N[n] \xleftrightarrow{\mathrm{FT}} \frac{2\pi}{N} \sum_{l=-\infty}^{\infty} \delta(\Omega - 2\pi l) δN[n]FT N2πl=−∞∑∞δ(Ω−2πl),和连续时间的冲激串信号 δ T ( t ) ↔ F T 2 π T ∑ l = − ∞ ∞ δ ( w − 2 π T l ) \displaystyle \delta_T(t) \xleftrightarrow{\mathrm{FT}} \frac{2\pi}{T} \sum_{l=-\infty}^{\infty} \delta(w - \frac{2\pi}{T} l) δT(t)FT T2πl=−∞∑∞δ(w−T2πl) 有相似的结构,证明方法同上。
2. 傅里叶变换(FT)与傅里叶级数(FS)的关系
傅里叶级数 (F ourier S eries cofficients) 的分析对象是周期的信号/序列,它和傅里叶变换之间联系的桥梁是 时域周期延拓, ∗ * ∗ 表示卷积运算。
以连续时间周期信号 x T ( t ) x_{_T}(t) xT(t) 为例,有 2 种方法来计算其 FT:
-
利用卷积性质
x ( t ) ∗ δ T ( t ) ↔ F T X ( j w ) 2 π T ∑ k = − ∞ ∞ δ ( w − 2 π T k ) = 2 π ∑ k = − ∞ ∞ 1 T X ( j 2 π T k ) δ ( w − 2 π T k ) x(t) * \textcolor{blue}{\delta_{T}(t)} \xleftrightarrow{\mathrm{FT}} X(jw) \textcolor{blue}{\frac{2\pi}{T} \sum_{k=-\infty}^{\infty}\delta(w-\frac{2\pi}{T}k) } = 2\pi \sum_{k=-\infty}^{\infty} \textcolor{red}{\frac{1}{T}X(j\frac{2\pi}{T}k)} \delta(w-\frac{2\pi}{T}k) x(t)∗δT(t)FT X(jw)T2πk=−∞∑∞δ(w−T2πk)=2πk=−∞∑∞T1X(jT2πk)δ(w−T2πk)
-
利用 FS 展开
x T ( t ) = ∑ k = − ∞ ∞ a k e j 2 π T k t ↔ F T ∑ k = − ∞ ∞ a k 2 π δ ( w − 2 π T k ) = 2 π ∑ k = − ∞ ∞ a k δ ( w − 2 π T k ) x_{_T}(t) = \sum_{k=-\infty}^{\infty} a_k e^{j\frac{2\pi}{T}kt} \xleftrightarrow{\mathrm{FT}} \sum_{k=-\infty}^{\infty} a_k \textcolor{blue}{2\pi \delta(w-\frac{2\pi}{T}k) } = 2\pi\sum_{k=-\infty}^{\infty} \textcolor{red}{a_k} \delta(w-\frac{2\pi}{T}k) xT(t)=k=−∞∑∞akejT2πktFT k=−∞∑∞ak2πδ(w−T2πk)=2πk=−∞∑∞akδ(w−T2πk)
对比两式,由 傅里叶变换的唯一性可得
a k = 1 T X ( j 2 π T k ) a_k = \frac{1}{T}X(j\frac{2\pi}{T}k) ak=T1X(jT2πk)
对于离散序列,也是类似的推导:
-
利用卷积性质
x [ n ] ∗ δ T [ n ] ↔ F T X ( j Ω ) 2 π N ∑ k = − ∞ ∞ δ ( Ω − 2 π N k ) = 2 π ∑ k = − ∞ ∞ 1 N X ( j 2 π N k ) δ ( Ω − 2 π N k ) x[n] * \textcolor{blue}{\delta_{T}[n]} \xleftrightarrow{\mathrm{FT}} X(j \Omega) \textcolor{blue}{\frac{2\pi}{N} \sum_{k=-\infty}^{\infty}\delta(\Omega-\frac{2\pi}{N}k) } = 2\pi \sum_{k=-\infty}^{\infty} \textcolor{red}{\frac{1}{N}X(j\frac{2\pi}{N}k)} \delta(\Omega-\frac{2\pi}{N}k) x[n]∗δT[n]FT X(jΩ)N2πk=−∞∑∞δ(Ω−N2πk)=2πk=−∞∑∞N1X(jN2πk)δ(Ω−N2πk)
-
利用 FS 展开
x N ( t ) = ∑ k = 0 N − 1 a k e j 2 π T k n ↔ F T ∑ k = 0 N − 1 a k 2 π ∑ l = − ∞ ∞ δ ( w − 2 π N k − 2 π l ) = 2 π ∑ k = 0 N − 1 a k ∑ l = − ∞ ∞ δ ( w − 2 π N k − 2 π l ) = 2 π ∑ k = 0 N − 1 a k ∑ l = − ∞ ∞ δ ( w − 2 π N ( k + N l ) ) = m = k + N l 2 π ∑ m = − ∞ ∞ a k δ ( w − 2 π N m ) \begin{aligned} x_{_N}(t) &= \sum_{k=0}^{N-1} a_k e^{j\frac{2\pi}{T}k n}\\ &\xleftrightarrow{\mathrm{FT}} \sum_{k=0}^{N-1} a_k \textcolor{blue}{2\pi \sum_{l=-\infty}^{\infty} \delta(w-\frac{2\pi}{N}k - 2\pi l) }\\ &= 2\pi\sum_{k=0}^{N-1} \textcolor{red}{a_k} \sum_{l=-\infty}^{\infty} \delta(w-\frac{2\pi}{N}k - 2\pi l)\\ &= 2\pi\sum_{k=0}^{N-1} \textcolor{red}{a_k} \sum_{l=-\infty}^{\infty} \delta\left(w-\frac{2\pi}{N}(k + N l)\right)\\ &\xlongequal{m=k+Nl} 2\pi \sum_{m=-\infty}^{\infty} \textcolor{red}{a_k} \delta\left(w-\frac{2\pi}{N}m \right)\\ \end{aligned} xN(t)=k=0∑N−1akejT2πknFT k=0∑N−1ak2πl=−∞∑∞δ(w−N2πk−2πl)=2πk=0∑N−1akl=−∞∑∞δ(w−N2πk−2πl)=2πk=0∑N−1akl=−∞∑∞δ(w−N2π(k+Nl))m=k+Nl2πm=−∞∑∞akδ(w−N2πm)
由 傅里叶变换的唯一性可得
a k = 1 N X ( j 2 π N k ) a_k = \frac{1}{N}X(j\frac{2\pi}{N}k) ak=N1X(jN2πk)
例子:
序列 x [ n ] = R 4 [ n ] = [ 1 , 1 , 1 , 1 ] ( 0 ) x[n]= R_4[n] = [1,1,1,1]_{(0)} x[n]=R4[n]=[1,1,1,1](0),对其进行周期延拓,周期为 4,得到周期序列 y [ n ] = ( R 4 [ n ] ) 4 y[n]=\left( R_4[n] \right)_4 y[n]=(R4[n])4,求 y [ n ] y[n] y[n]的 FS。
-
根据定义计算: a k = 1 4 ∑ n = 0 3 y [ n ] e − j π 2 k n = 1 4 ⋅ 4 δ [ k ] = δ [ k ] a_k = \displaystyle\frac{1}{4}\sum_{n=0}^{3} y[n] e^{-j\frac{\pi}{2}kn} = \frac{1}{4}\cdot 4\delta[k] = \delta[k] ak=41n=0∑3y[n]e−j2πkn=41⋅4δ[k]=δ[k]
-
根据 FT 计算:
F T ( x [ n ] ) = ∑ n = − ∞ ∞ x [ n ] e − j w n = ∑ n = 0 3 e − j w n = 1 + e − j w + e − j 2 w + e − j 3 w \begin{aligned} \mathrm{FT}{(x[n])} &= \sum_{n=-\infty}^{\infty} x[n] e^{-jwn}\\ &= \sum_{n=0}^{3} e^{-jwn}\\ &= 1 + e^{-jw} + e^{-j2w} + e^{-j3w} \end{aligned} FT(x[n])=n=−∞∑∞x[n]e−jwn=n=0∑3e−jwn=1+e−jw+e−j2w+e−j3w
由 a k = 1 N X ( j 2 π N k ) \displaystyle a_k = \frac{1}{N}X(j\frac{2\pi}{N}k) ak=N1X(jN2πk) 得
a 0 = 1 4 ( 1 + e − j ⋅ 0 + e − j 2 ⋅ 0 + e − j 3 ⋅ 0 ) = 1 a 1 = 1 4 ( 1 + e − j ⋅ π 2 + e − j 2 ⋅ π 2 + e − j 3 ⋅ π 2 ) = 0 a 2 = 1 4 ( 1 + e − j ⋅ π + e − j 2 ⋅ π + e − j 3 ⋅ π ) = 0 a 3 = 1 4 ( 1 + e − j ⋅ 3 π 2 + e − j 2 ⋅ 3 π 2 + e − j 3 ⋅ 3 π 2 ) = 0 \begin{aligned} a_0 &= \frac{1}{4} (1 + e^{-j\cdot 0} + e^{-j2\cdot 0} + e^{-j3\cdot 0}) = 1\\ a_1 &= \frac{1}{4} (1 + e^{-j\cdot \frac{\pi}{2}} + e^{-j2\cdot \frac{\pi}{2}} + e^{-j3\cdot \frac{\pi}{2}}) = 0\\ a_2 &= \frac{1}{4} (1 + e^{-j\cdot \pi} + e^{-j2\cdot \pi} + e^{-j3\cdot \pi}) = 0\\ a_3 &= \frac{1}{4} (1 + e^{-j\cdot \frac{3\pi}{2}} + e^{-j2\cdot \frac{3\pi}{2}} + e^{-j3\cdot \frac{3\pi}{2}}) = 0\\ \end{aligned} a0a1a2a3=41(1+e−j⋅0+e−j2⋅0+e−j3⋅0)=1=41(1+e−j⋅2π+e−j2⋅2π+e−j3⋅2π)=0=41(1+e−j⋅π+e−j2⋅π+e−j3⋅π)=0=41(1+e−j⋅23π+e−j2⋅23π+e−j3⋅23π)=0
结果与根据定义计算的结果相同。y [ n ] y[n] y[n] 实际是一个直流序列,它的周期可以不是 4,如 1 , 2 , 3 , 5 ⋯ 1,2,3,5\cdots 1,2,3,5⋯,不同周期的 FS 都可以写为 a k = δ [ k ] a_k=\delta[k] ak=δ[k]。 为保证唯一性,傅里叶级数不能单单只看数值,还应该包含信号/序列的基频/周期,才能完整且唯一地表示原信号。
对于连续时间周期信号,FS 有无限项,但是每项代表一个频率分量;对于离散时间周期序列;FS 是有限的、周期的,FS 的个数代表了的原信号的周期。