Xilinx-Verilog-学习笔记(19):正弦波信号发生器与DDS
Xilinx-Verilog-学习笔记(19):正弦波信号发生器与DDS
一、正弦波信号发生器
1、浮点数的定点化
这里以2.918为例,实现浮点数向定点数的转换:
(1)在进行浮点转定点之前,要先确定整数部分位宽和小数部分位宽。3位整数位宽,12位的小数位宽,最高位的符号位1位。
(2)15位宽的数能够表示的数值范围为-32768到32767。整数部分3位宽的数最大能表示到8,因此最大精度为8/32767=0.000244140625。
(3)2.918进行定点化的过程为2.918/(8/32768)=11952.128~=11952这个值就是定点后的2.918的值。而最后的0.128就是定点化会带来量化误差。
2、用matlab生成正弦波并进行量化处理
量化处理
量化在数字信号处理领域,是指将信号的连续取值(或者大量可能的离散取值)近似为有限多个(或较少的)离散值的过程。
正弦波量化思想
本实验通过256个位宽为8的数据对正弦信号进行采样,以对一个周期的正弦信号进行量化处理。每个数据位宽为8,相当于把正弦信号的幅度从-1到1进行256份等间隔划分;采样点数为256个,相当于对一个正弦周期等间隔地采样了256个点。
量化后的数据由256个介于-1到1之间的数构成,之后将浮点型的数值进行定点化的转换,使其为0~256之间的整数。(具体处理方法见代码)
MatLab代码:
clc;
clear all;
N=2^8;
s_p=0:255;%正弦波一个周期的采样点数
sin_data=sin(2*pi*s_p/N);%256个介于-1到1之间的数
%打印我们的波形
% plot(sin_data,'r*');
% hold on;
% plot(sin_data);
%定点化
fix_p_sin_data=fix(sin_data*127);%256个介于-128到127之间的数
for i=1:N
if fix_p_sin_data(i)<0
fix_p_sin_data(i)=N+fix_p_sin_data(i);%将负数搬到128到256之间(用255加即可)
else
fix_p_sin_data(i)=fix_p_sin_data(i);%整数不用管
end
end
%以下是生成mif文件,用于RAM的初始化
fid=fopen('sp_ram_256x8.mif','w+');
fprintf(fid,'WIDTH=8;\n');
fprintf(fid,'DEPTH=256;\n');
fprintf(fid,'ADDRESS_RADIX=UNS;\n');
fprintf(fid,'DATA_RADIX=UNS;\n');
fprintf(fid,'CONTENT BEGIN \n');
for i=1:N
fprintf(fid,'%d:%d; \n',i-1,fix_p_sin_data(i));
end
fprintf(fid,'END; \n');
fclose(fid);
通过sin_data=sin(2 * pi * s_p/N); 即可实现对一个正弦周期的量化。

3、design文件
module ex_dds(
input wire sclk,
input wire rst_n,
output wire [7:0] o_wave
);
reg [7:0] addr;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
addr <= 'd0;
else
addr <= addr + 1'b1;
sp_ram_256x8 sp_ram_256x8_inst (
.address ( addr ),
.clock ( sclk ),
.data ( 8'd0 ),
.wren ( 1'b0 ),
.q ( o_wave )
);
endmodule
其中例化的深度256,位宽为8的RAM是直接调用IP核产生的。
4、testbench文件
`timescale 1ns/1ns
module tb_ex_dds;
reg sclk,rst_n;
wire [7:0] o_wave;
initial begin
sclk =0;
rst_n=0;
#100
rst_n =1;
end
always #10 sclk =~sclk;//50Mhz
ex_dds ex_dds_inst(
.sclk (sclk),
.rst_n (rst_n),
.o_wave (o_wave)
);
endmodule
5、仿真波形
将RAM输出的数值用模拟波形表示出来,可以看出是正弦信号。对于地址是锯齿波,因为是从0到255然后再到0。
二、DDS直接频率合成器
1、基本原理
- fc为每秒钟累加多少次,2^n为累加器能够累加到的最大范围,所以fc/2 ^n为每秒钟累加器会溢出多少次,即为周期(分辨率)。提高相位累加器的位宽n可以调高频率分辨率。
- 存储正弦的RAM深度或者叫正弦波一个周期量化的点数,量化的点数越多生成的正弦波相位噪声低。
- M是控制字,通过频率控制字来产生不同的频率。
这里相位累加寄存器的位宽为32,目标实现1Mhz的信号:
(1)控制字设置:1e6=M * 50e6/2^32,则M=1e6 * 2^32/50e6~=85899345.
(2)相位累加器为32位,而最终输出为8位,为了取整数倍,因此取相位累加器的高8位。
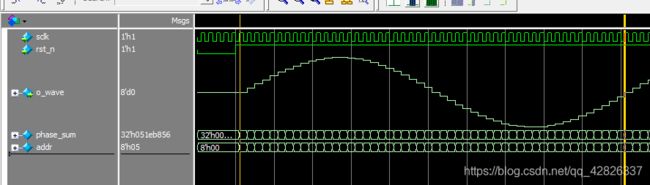
可以得到1Mhz的正弦周期。因此,通过修改M的值可以调节正弦信号的频率。
于是我们可以设计过一段时间将M的值增大一定值,即可实现频率的连续变换:
2、design文件
module ex_dds(
input wire sclk,
input wire rst_n,
output wire [7:0] o_wave
);
parameter FRQ_W=32'd85899346; //相当于M
parameter FRQ_ADD=32'd85899346/2; //相当于递增量
reg [31:0] phase_sum;
wire [7:0] addr;
reg [31:0] frq_word;
reg [6:0] div_cnt;
reg div_flag;
//记100个时钟周期,M的值递增一次
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
div_cnt <= 1'b0;
else if(div_cnt == 7'd99)
div_cnt <= 1'b0;
else
div_cnt <= div_cnt + 1'b1;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
div_flag <= 1'b0;
else if(div_cnt == 7'd99)
div_flag <= 1'b1;
else
div_flag <= 1'b0;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
frq_word <= FRQ_W;
else if(div_flag == 1'b1)
frq_word <= frq_word + FRQ_ADD;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
phase_sum <= 'd0;
else
phase_sum <= phase_sum + frq_word;
assign addr = phase_sum[31:24];
/* always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
addr <= 'd0;
else
addr <= addr + 1'b1; */
sp_ram_256x8 sp_ram_256x8_inst (
.address ( addr ),
.clock ( sclk ),
.data ( 8'd0 ),
.wren ( 1'b0 ),
.q ( o_wave )
);
endmodule
此时通过计数器,实现100个时钟周期变频一次。
如果用于高速电路的话,不要直接用分频器作为标志,可以通过定义一个div_flag作为标志。
3、仿真波形
三、混频器
混频器的主要任务是将两个不同频率的信号进行叠加。
1、MatLab代码
(1)首先定义好采样率,两个时钟的频率,从图中可以看出,红色的时钟频率是蓝色的5倍。
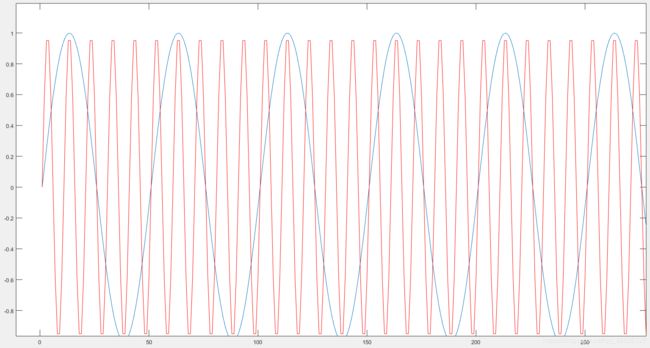
(2)然后是混频,混频后的到的信号包含两个频率分量,一个是f1+f2,一个是f1-f2,即一个6Mhz,一个4Mhz。从时域信号中我们难以看出结果是否正确,因此需要对其进行FFT变换,从频域分析。

前1024个点表示正频域,后1024个点表示复频域,因此只需要看前1024个即可。
频率分辨率与FFT计算的点数N、采样频率fs都有关。频率分辨率=fs/N
50M/2048=0.0244Mhz,这是FFT中能够分辨出的最低的频率,用0.0244*1024=25Mhz,正好是50Mhz采样频率能够识别出来的频率。
两个峰的点分别是165和247,0.0244 *165=4Mhz,0.0244 * 247=6Mhz,正好是混频后的两个频率分量。
clc;
clear all;
fs=50e6; %50Mhz采样率
f1=1e6; %1Mhz频率
f2=5e6; %5Mhz频率
n=0:2047;
s_1=sin(2*pi*n*f1/fs);
s_2=sin(2*pi*n*f2/fs);
%s_1和s_2混频,就是相乘
s_12=s_1.*s_2; %混频后包含两个频率分量,一个是f1+f2一个是f1-f2
%频域分析
fft_out=fft(s_12,2048);
fft_abs=abs(fft_out);
2、design文件
本实验设计1Khz的正弦信号和10Khz的正弦信号进行混频。
通过计算:
(1)1Khz:M=1000 * 2^32/50e6=85899
(2)10Khz:M=10000 * 2^32/50e6=858993
module ex_dds(
input wire sclk,//50Mhz
input wire rst_n,
output wire [15:0] o_wave
);
parameter FRQ_W_1k=32'd85899;
parameter FRQ_W_10k=32'd858993;
reg [31:0] phase_sum_1k,phase_sum_10k;
wire [7:0] addr_1k,addr_10k;
wire [7:0] o_wave_1k;
wire [7:0] o_wave_10k;
//
reg [22:0] sum;
reg [14:0] sum_cnt;
reg sum_flag;
reg [22:0] sum_r;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
sum_cnt <= 'd0;
else if(sum_cnt == 'd29999)
sum_cnt <='d0;
else
sum_cnt <= sum_cnt + 1'b1;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
sum_flag<= 1'b0;
else if(sum_cnt == 'd29999)
sum_flag <= 1'b1;
else
sum_flag <= 1'b0;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
sum <= 'd0;
else if(sum_flag == 1'b1)
sum <= {{15{o_wave_1k[7]}},o_wave_1k};
else
sum <= sum + {{15{o_wave_1k[7]}},o_wave_1k};
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
sum_r <= 'd0;
else if(sum_flag == 1'b1)
sum_r <= sum;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
phase_sum_1k<='d0;
else
phase_sum_1k <= phase_sum_1k + FRQ_W_1k ;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
phase_sum_10k<='d0;
else
phase_sum_10k <= phase_sum_10k + FRQ_W_10k ;
assign addr_1k=phase_sum_1k[31:24];
assign addr_10k=phase_sum_10k[31:24];
//混频器
mult_8x8_l0 mult_8x8_l0_inst (
.dataa ( o_wave_1k ),
.datab ( o_wave_10k ),
.result ( o_wave )
);
sp_ram_256x8 sp_ram_256x8_inst (
.address ( addr_1k ),
.clock ( sclk ),
.data ( 8'd0 ),
.wren ( 1'b0 ),
.q ( o_wave_1k )
);
sp_ram_256x8 sp_ram_256x8_inst_1 (
.address ( addr_10k ),
.clock ( sclk ),
.data ( 8'd0 ),
.wren ( 1'b0 ),
.q ( o_wave_10k )
);
endmodule
该模块中通过例化两个RAM来生成两个正弦波形,通过例化一个乘法器来实现两个正弦信号的混频。
3、testbench文件
`timescale 1ns/1ns
module tb_ex_dds;
reg sclk,rst_n;
wire [15:0] o_wave;
initial begin
sclk =0;
rst_n=0;
#100
rst_n =1;
end
always #10 sclk =~sclk;//50Mhz
ex_dds ex_dds_inst(
.sclk (sclk),
.rst_n (rst_n),
.o_wave (o_wave)
);
endmodule



