C均值聚类算法

聚类算法

有兴趣请关注我的博客https://blog.csdn.net/qq_40731414
朱朱朱朱红喜的邮箱[email protected]

1.实验要求：

请使用C均值聚类方法对数据集进行聚类，给每个样本一个类别标签，并画出聚类结果（参考图trainning sample的画法），并与其真实标签（在truelabel.mat中）进行对比，计算聚类的准确率；

3.算法思想

采用距离作为相似性指标，从而发现给定数据集中的K个类，且每个类的中心是根据类中所有值的均值得到，每个类用聚类中心来描述。对于给定的一个包含n个d维数据点的数据集X以及要分得的类别K,选取欧式距离作为相似度指标，聚类目标是使得各类的聚类平方和最小，聚类中心为对应类别中各数据点的平均值，同时为了使得算法收敛，在迭代过程中，应使最终的聚类中心尽可能的不变 。

3.算法基本步骤

• 在样本集合中选择C个点作为初始类中心；

• 在剩下的样本点中选择一个，计算其到各个中心点的距离，选取距离最短者将其归为那个类别；

• 选择下一个样本，重复2直到计算完所有样本，若集合不发生变化或达到迭代上限则转5否则转4；

• 根据当前的类划分情况重新计算中心点，重复步骤2；

• 结束算法。

4.算法实现（Python）

• 主文件 C-means.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2019/6/16 13:58
# @Author  : 朱红喜
# @File    : C-means.py
# @Software: PyCharm

import numpy as np
from ClassifyHandle import ClassifyHandle
from FileUtil import FileUtil
from PlotUtil import PlotUtils

class_number = 3  # 按照老师的给的数据图  把150个数据分为三类
datas = FileUtil.open_matfile("data4train.mat")  # 数据集
centers = []  # 聚类中心

# 选取三个数据作为三个初始聚类中心
for i in range(class_number):
    centers.append(datas[i])

# 将数据集分类到三个类中
result = ClassifyHandle.classify(centers, datas)


print("######################第一次分类（初始）结果#########################")
print(result)

# 画出散点图
PlotUtils.plot(result)

end_flag = 1  # 循环标志

# 循环计算各类中心并重新分类直到无法再分类，结束循环
while end_flag:
    new_centers = []  # 新的分类中心

    #  通过分类结果计算获得新的分类中心
    for i in range(result.__len__()):
        new_centers.append(ClassifyHandle.get_new_center(result[i]))
        
    PlotUtils.single_plot(new_centers)

    # 如果新的分类中心与原来的分类中心相同说明分类结束，循环结束
    # if new_centers == centers:
    if np.array_equal(new_centers, centers):
        end_flag = 0
    else:
        centers = new_centers.copy()

    result = ClassifyHandle.classify(centers, datas)

    # 画出散点图
    # PlotUtils.plot(result)

# 将结果输出
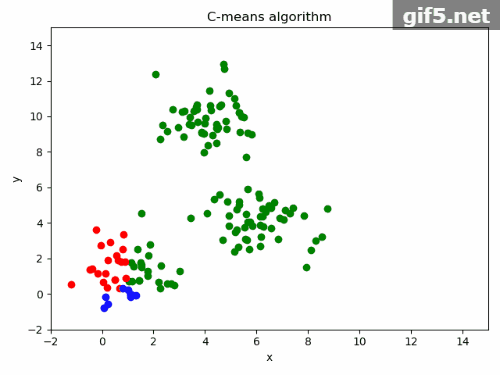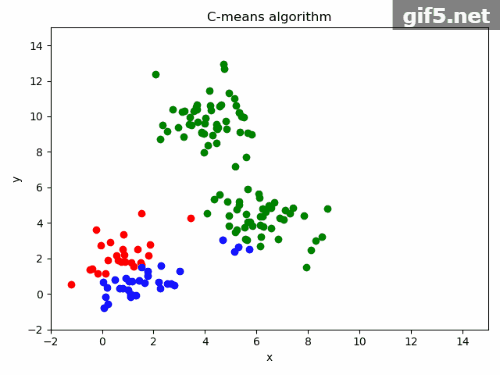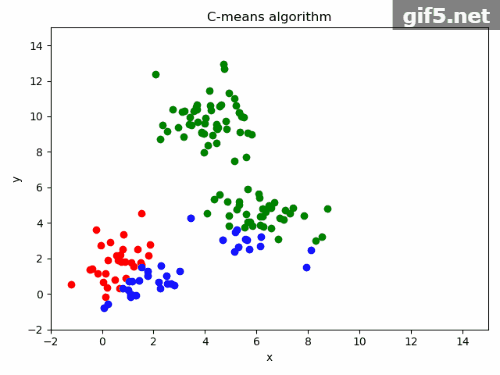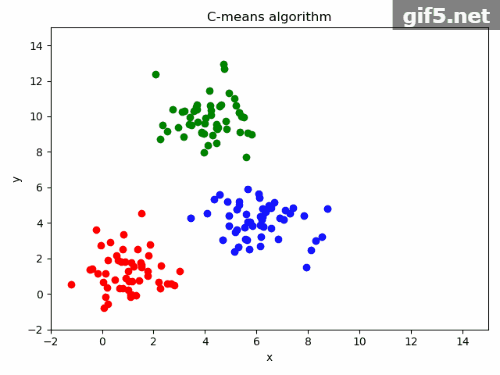
print("######################最终的分类结果#########################")
print(result)

# 将数据输出到mat文件
FileUtil.save_matflie("cmeans_result.mat", result)

# 画出散点图
PlotUtils.plot(result)

• 分类与计算新的类中心 ClassifyHandle.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2019/6/16 15:07
# @Author  : 朱红喜
# @File    : ClassifyHandle.py
# @Software: PyCharm

from MathUtil import MathUtil


class ClassifyHandle:

    # 将每个数据分类
    @staticmethod
    def classify(centers, datas):
        result = []
        for i in range(centers.__len__()):
            result.append([])
            result[i].append(centers[i])

        for i in range(datas.__len__()):

            min_distance = float('inf')  # 初始化最小距离
            class_index = 0  # 每个类别下标

            for j in range(centers.__len__()):

                # 依次计算每个数据到每一个类中心的欧式距离
                # 根据欧式距离分类
                distance = MathUtil.compute_distance(centers[j], datas[i])
                if min_distance > distance:
                    min_distance = distance
                    class_index = j

            # 将属于这个类别的数据加入这个类中
            result[class_index].append(datas[i])

        return result

    # 计算每一个类的中心
    @staticmethod
    def get_new_center(datas):

        # 初始类中心，默认就是第一个位置的数据点
        # 即计算聚类中的所有数据点的各自维度的算术平均数
        data = datas[0].copy()

        # 遍历本类的所有数据
        for i in range(datas.__len__()):

            # 每个数据是二维的，遍历每个维度，将各自维度求和
            for j in range(data.__len__()):
                data[j] += datas[i][j]

        # 求每个维度和的算术平均
        for k in range(data.__len__()):
            data[k] /= datas.__len__()
        return data

• 计算二维欧式距离 MathUtil.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2019/6/16 14:20
# @Author  : 朱红喜
# @File    : MathUtil.py
# @Software: PyCharm
import math


class MathUtil:

    # 计算二维欧式距离
    @staticmethod
    def compute_distance(data, center):
        distance = 0

        # 每个数据包含二维的数据，计算二维的欧式距需要循环两次
        # math.sqrt（(x_1-y_1)**2+(x_2-y_2)**2)
        for i in range(data.__len__()):
            # distance += (data[i] - center[i]) ** 2
            distance += math.pow((data[i] - center[i]), 2)
        distance = math.sqrt(distance)
        return distance

• 读取和保存mat文件 FileUtil.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2019/6/16 14:20
# @Author  : 朱红喜
# @File    : FileUtil.py
# @Software: PyCharm

import scipy.io as sio
import numpy as np
import matplotlib.pyplot as plt


# 文件读写操作类


class FileUtil:

    # 读取mat文件，获得数据
    @staticmethod
    def open_matfile(filename):
        # "data4train.mat"
        #  读出来的字典类型
        mat_data = sio.loadmat(filename)

        # 测试下mat文件到底输出了什么
        # 键值对形式的同时 还会有附加信息
        # for key, value in mat_data.items():
        #     print(key, ':', value)

        # 取出有用的矩阵数据集
        datas = mat_data['data4train']
        # print(datas)

        # 转置，每一行为一个记录，每一列为一个字段
        datas = datas.T
        print(datas)
        return datas

    # 将结果保存到mat文件中
    @staticmethod
    def save_matflie(filename, result):
        sio.savemat(filename, {'result': result})  # "cmeans_result.mat"

• 画散点图封装类 PlotUtil.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2019/6/28 12:13
# @Author  : 朱红喜
# @File    : PlotUtil.py
# @Software: PyCharm

from ColorSelect import ColorSelect
import matplotlib.pyplot as plt


class PlotUtils:

    # 画出结果散点图
    @staticmethod
    def plot(result):
        # 画出散点图
        plt.title("C-means algorithm")
        plt.xlim(-2, 15)
        plt.ylim(-2, 15)
        plt.xlabel("x")
        plt.ylabel("y")

        for i in range(result.__len__()):

            for j in range(result[i].__len__()):
                print(i, end='')
                plt.plot(result[i][j][0], result[i][j][1], ColorSelect.color_select(i))
        plt.show()

    @staticmethod
    def single_plot(centers):

        # 画出类中心点
        plt.title("C-means algorithm")
        plt.xlim(-2, 15)
        plt.ylim(-2, 15)
        plt.xlabel("x")
        plt.ylabel("y")
        for i in range(centers.__len__()):
            plt.plot(centers[i][0], centers[i][1],  ColorSelect.color_select(i))
        plt.show()

• 颜色筛选器 ColorSelect.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2019/6/17 17:39
# @Author  : 朱红喜
# @File    : ColorSelect.py
# @Software: PyCharm


class ColorSelect:

    # 颜色筛选器
    @staticmethod
    def color_select(index):
        color_dict = {0: 'go', 1: 'ro', 2: 'bo'}
        return color_dict[index]

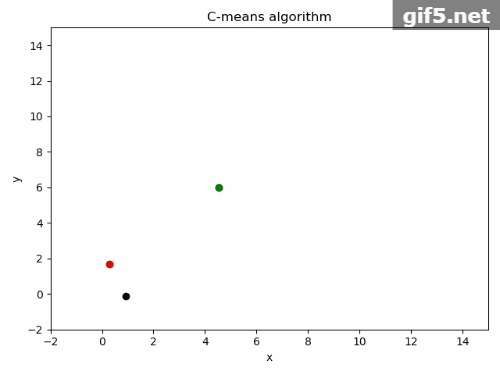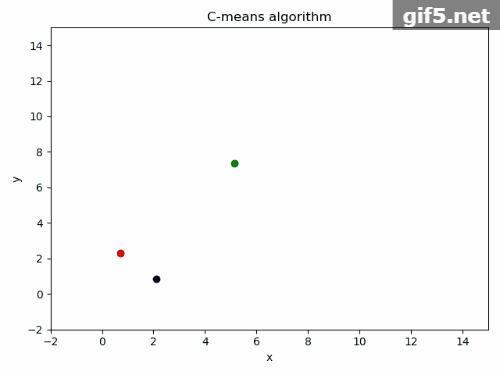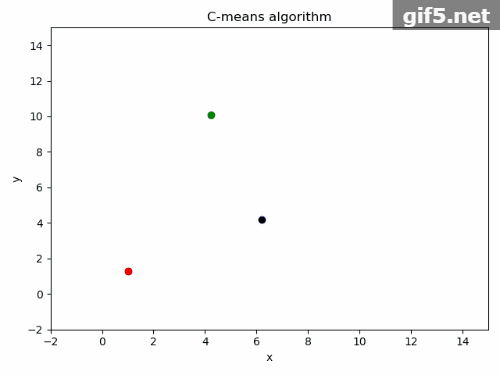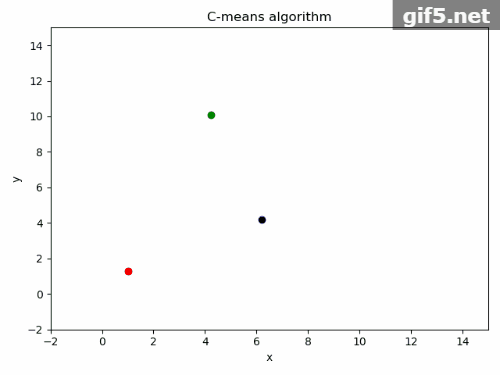
5.运行结果

• 聚类过程
  
• 类心变化过程
  

6.相关数据

• 输入数据 （将老师给的数据转置了的）
  [[ 1.43637539 0.74944716]
  [ 0.49563752 0.81009835]
  [ 1.10210771 -0.03291351]
  [ 2.19625054 0.67670808]
  [ 1.12028282 1.76652685]
  [-0.0368434 2.74467318]
  [ 0.14289676 -0.16051993]
  [ 0.8301257 3.37741185]
  [ 0.80833172 2.52607796]
  [ 0.13418479 1.1685075 ]
  [ 1.18066413 0.69879347]
  [ 2.26652848 0.30134573]
  [ 0.74883071 1.83277058]
  [ 0.79542995 0.30539475]
  [-1.20152191 0.53811701]
  [ 0.2254869 1.88361714]
  [-0.39327258 1.43594418]
  [ 0.61376535 1.89674736]
  [ 1.52558635 1.50473203]
  [ 2.52326928 0.59910286]
  [ 2.79849445 0.48615199]
  [ 0.88311573 1.7963676 ]
  [ 0.67980381 0.32880984]
  [ 1.81751628 2.18665904]
  [ 1.49015919 1.79070197]
  [ 1.76525116 1.28772149]
  [ 1.77827905 1.00322611]
  [-0.48030517 1.36561719]
  [ 1.54036396 4.52667782]
  [ 0.90846098 0.88756334]
  [ 0.23974762 -0.55659393]
  [ 0.30640456 2.9151023 ]
  [ 2.28145775 1.60984605]
  [ 0.19026239 0.35208838]
  [-0.23681835 3.61733491]
  [ 1.21468645 1.55095042]
  [ 3.01077177 1.29420368]
  [ 1.02555443 0.2221562 ]
  [ 1.30829944 -0.0649301 ]
  [ 0.06175279 -0.76841403]
  [ 2.67421595 0.57708046]
  [ 1.12498817 -0.05310243]
  [ 1.53010126 1.64775524]
  [ 0.04793178 0.68237181]
  [ 1.85404282 2.76899157]
  [ 1.38914573 2.5105824 ]
  [-0.15600108 1.16401032]
  [ 1.03974013 0.71723629]
  [ 0.5494014 2.15216581]
  [ 1.10924794 -0.14650763]
  [ 6.6736987 5.166475 ]
  [ 5.330887 5.21282142]
  [ 5.5996773 4.48554099]
  [ 5.32819757 5.02601649]
  [ 6.57562902 4.87072602]
  [ 5.22190648 3.61824212]
  [ 4.9364388 4.42889303]
  [ 6.5529783 3.70086948]
  [ 5.57657116 3.10013148]
  [ 6.36158716 4.63474546]
  [ 5.64811076 4.06745359]
  [ 6.26954071 3.81287946]
  [ 3.43555064 4.29172746]
  [ 6.46586413 4.98769469]
  [ 7.85356094 4.39293457]
  [ 7.03928934 4.19455137]
  [ 6.91089658 4.27978496]
  [ 5.76026871 4.05122031]
  [ 6.18099808 3.22553376]
  [ 6.24424955 4.78678171]
  [ 6.09639288 5.40890695]
  [ 5.1695315 3.46590142]
  [ 5.64774781 5.92775843]
  [ 5.82522496 3.82375245]
  [ 5.51934658 3.75624964]
  [ 6.83683671 3.10239934]
  [ 8.53834934 3.20766313]
  [ 4.67666575 3.04702531]
  [ 6.12834026 4.35390545]
  [ 4.55762085 5.59702632]
  [ 7.30250821 4.52747025]
  [ 7.4099115 4.8542023 ]
  [ 4.33745703 5.34184652]
  [ 7.94368448 1.50046656]
  [ 4.91530155 3.83244068]
  [ 6.22681898 4.35301531]
  [ 7.0989292 4.71725373]
  [ 6.14718875 2.69514836]
  [ 8.29566581 2.99413105]
  [ 8.75255788 4.79068347]
  [ 6.13831772 3.88342867]
  [ 4.09293379 4.55308989]
  [ 5.63500701 3.0393552 ]
  [ 5.15188999 2.3661976 ]
  [ 5.23524664 4.76120028]
  [ 4.87230519 5.19330715]
  [ 6.0781889 5.63205722]
  [ 8.10662966 2.4678104 ]
  [ 5.28415261 2.6631476 ]
  [ 5.71948434 2.5261535 ]
  [ 3.95833693 7.97163804]
  [ 3.38449266 9.55074319]
  [ 5.31415481 10.2359932 ]
  [ 2.54493342 9.16482704]
  [ 2.25765078 8.72404484]
  [ 4.20530468 10.61703508]
  [ 5.1929304 10.6127015 ]
  [ 3.1971769 10.28938116]
  [ 2.73436358 10.39531612]
  [ 3.85066865 9.12943716]
  [ 2.36355332 9.50231162]
  [ 4.01734435 9.89332818]
  [ 4.82838727 9.31217086]
  [ 4.21773835 10.33188088]
  [ 2.0907551 12.36522474]
  [ 3.46317818 9.51776928]
  [ 3.6979677 10.64744821]
  [ 5.81358213 8.96557528]
  [ 4.91485175 11.3395546 ]
  [ 3.94291928 9.03085964]
  [ 5.30936208 10.2087156 ]
  [ 2.95526415 9.38140664]
  [ 3.65173319 10.51201564]
  [ 5.41256116 10.01135417]
  [ 5.50238293 9.95601137]
  [ 4.73037599 12.94909254]
  [ 4.49075227 9.36995381]
  [ 3.41387386 9.9531206 ]
  [ 4.74489965 12.68302551]
  [ 3.17184503 8.85330931]
  [ 4.57452073 10.55299875]
  [ 4.28184138 8.92354159]
  [ 5.13930627 11.03063958]
  [ 3.57413215 10.32752981]
  [ 4.63613989 10.65212481]
  [ 4.79317808 9.72113888]
  [ 3.10162289 10.24519159]
  [ 4.15624484 11.47251348]
  [ 5.59725391 7.72489846]
  [ 4.11243971 8.36670928]
  [ 3.69137507 10.41546894]
  [ 4.45665961 9.34523115]
  [ 3.72489917 9.70365168]
  [ 4.44314361 8.50308112]
  [ 3.86523487 9.09516555]
  [ 3.98167177 9.59581845]
  [ 4.46078943 9.27420183]
  [ 5.36231546 9.13351497]
  [ 4.45187457 9.57815322]
  [ 5.64838366 9.05733368]]

作者:朱红喜
转载请注明出处
参考博客：https://blog.csdn.net/aaalswaaa1/article/details/81675679
https://blog.csdn.net/weixin_40938820/article/details/82559991
https://blog.csdn.net/zb1165048017/article/details/48579743
https://blog.csdn.net/u011591807/article/details/84349181
https://www.cnblogs.com/kylinlin/p/5299078.html