方差分析（ANOVA）分类、应用举例及matlab代码

目录

一、介绍

1.1、定义

1.2、为什么使用方差分析？

1.3、方差分析的分类

1.3.1、按影响分析指标的因素个数

1.3.2、按分析指标的个数

1.3.3、多因素多分析指标

二、单因素一元方差分析（anova1）

2.1、问题

2.2 步骤

2.3 MATLAB代码

2.4 单因素方差分析的MATLAB全部代码

三、双因素一元方差分析（anova2）

3.1、问题

3.2 步骤

3.3 MATLAB代码

四、多因素一元方差分析（anovan）

4.1、问题

4.2 MATLAB代码

---

一、介绍

1.1、定义

方差分析是英国统计学家R.A.Fisher在20世纪20年代提出的一种统计方法，它有着非常广泛的应用。
方差分析（analysis of variance, ANOVA）是一种统计检验，用于检验两组或更多组样本的均值是否相同。

1.2、为什么使用方差分析？

t检验涉及一组或者两组样本的均值检验，而在三个或者更多组的均值比较中（例：检验脑电信号功率的平均值是否会因为记录时间（早上，上午和晚上）不同而不同），t检验并不是一种有效的统计检验工具，而且也可能导致结果出现偏差（如果反复使用t-检验，两两之间t检验，则会导致严重的第一类错误）。
方差分析能够在不增加第一类错误发生率的情况下测试几组样本均值之间是否存在差异。

1.3、方差分析的分类

1.3.1、按影响分析指标的因素个数

方差分析按影响分析指标的因素(也可简单成为 自变量)个数的多少，分为单因素方差分析（one-way ANOVA）、双因素方差分析、三因素方差分析 （两个或多个因素，称为多因素方差分析，multi-way ANOVA）。
在多因素方差分析中，把单个因素在不同水平下产生的不同实验结果成为主效应（main effect）;把多个因素间在不同水平共同产生的实验结果差别称为交互效应（interaction effect）。
与配对样本t检验（paired-samples t-test）类似（例，睁眼条件下静息态脑电信号功率的均值与闭眼条件下脑电信号功率的均值是否有显著差异），如果方差分析中某一因素的不同水平的测量来自同一组被试，则检验称为重复测量的方差分析（repeated measures ANOVA）,该因素（闭眼 or 睁眼）称为重复测量因素（repeated meausres factor）或者被试内因素（within-subjects factor）。
也类似于独立双样本t检验（independent two-samples t-test）（例：检验男性被试和女性被试在睁眼条件下静息态脑电信号功率的均值是否有显著差异），在方差分析中如果某个因素在不同水平的测试来自不同组的被试，则称该因素（男性 or 女性）为被试间因素（between-subjects factor）。

1.3.2、按分析指标的个数

方差分析按分析指标（也可简单称为 因变量）的个数多少，分为一元方差分析（即ANOVOA）、多元方差分析（即，MANOVOA）。

1.3.3、多因素多分析指标

多自变量多因变量的方差分析，可以简单称为多元方差分析，当然更精确的称为“X因素Y元方差分析”，如二因素二元方差分析。

二、单因素一元方差分析（anova1）

p = anova1(x)

研究一个控制变量的不同水平是否对观测变量产生了显著影响。

2.1、问题

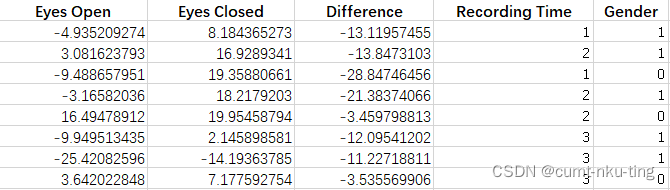
检验不同时间记录（早晨，下午和晚上）的睁眼状态下的静息脑电信号平均功率的均值是否相同。

 样本X满足方差分析的几个基本假定：所有样本均来自正态总体；这些正态总体具有相同的方差。

2.2 步骤

• 正态性检验

H0：不同时间所记录的睁眼状态下的静息脑电信号平均功率值服从正态分布；H1：不服从正态分布

• 方差齐次性检验

H0：不同时间所记录的睁眼状态下的静息脑电信号平均功率值服从方差相同的正态分布；H1：不服从方差相同的正态分布

• 方差分析
  • 建立假设检验
    •     H0：不同时间所记录的睁眼状态下的静息脑电信号平均功率的均值是相同的。
          H1：不同时间所记录的睁眼状态下的静息脑电信号平均功率的均值是不相同的，三个之中至少有两个不等。
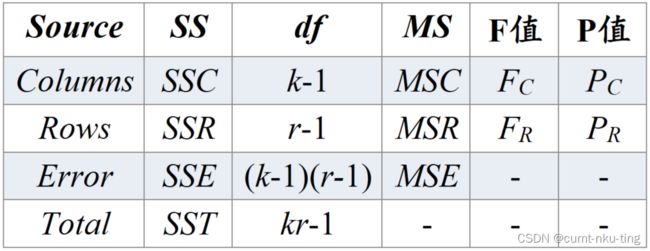
  • 统计F值
    • 
    • 
    • 
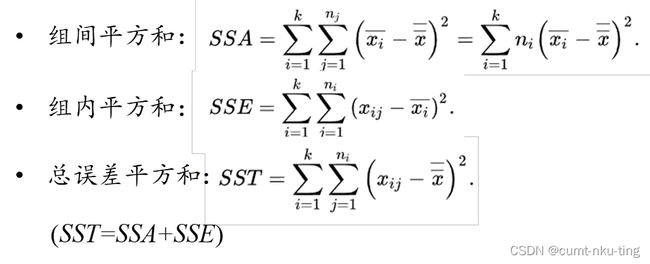
    • 首先计算均值：第i个总体的样本均值和总均值，ni为第i个总体的样本观察值个数；然后计算误差平方和。
          组间平方和SSA，各组平均值与总平均值的误差平方和，反映了各水平总体的样本均值之间的差异程度，表示因素A的各个水平理论平均值的不同带来的影响，记为“因素A的平方和”或“组间差异”；
          组内平方和SSE，它是各组的各样本数据与其组平均值误差的平方和，反映了每个样本各观察值的离散状况，表示随机误差的影响，记为“误差平方和”或“组内差异”；
          总误差平方和SST，它是全部观察值与总平均值的误差平方和，反映全部观察值的离散程度。
          组间均方和组内均方分别由误差平方和除以各自的自由度得到。
      MSA/MSE比值构成F分布。
  • 确定p值并做出统计决策
    • 计算出统计量F的值后，根据给定的显著性水平α, 在F分布表中查找分子自由度为(k-1)、分母自由度为n-k的相应临界值Fα。
    • 
• 多重比较
  • 若不同时间水平下的具有显著差异，但是也并不意味着任意两个时间水平下的脑电信号功率具有显著差异，因此还需要进行两两之间的比较检验，即多重比较，找出脑电信号功率存在显著差异的时间。

  • 即便不同时间的脑电信号功率之间不具有显著差异，但在实际应用中，有两点还可以再考察以下：

    • 各个水平理论平均值的点估计之间的差异如何，若这个差异没有大到有实际意义的程度，则加强了上述结论，即各个水平之间的差异即使存在，其实际意义也有限。

    • 若不同水平之间均值的差异，从应用观点看，达到了比较重要的程度，则原假设H0之所以被接受，是由于随机误差的影响太大。误差方差2的一个无偏估计量是，可以考察一下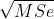的值。若从应用的角度看这个值太大，则看来本试验在精度上欠理想。如条件允许，应考虑增大试验规模，以及改进试验，以图尽量虽小随机误差的影响。

2.3 MATLAB代码

• 正态性检验

  • clc;clear;close all;
    [num,txt,raw] = xlsread('Resting State.xlsx');
    %% one-way ANOVA
    x=num(:,1);
    group=num(:,4);
    %正态性检验
    for i=1:3
        x_i=x(group==i); %提取第i个group的睁眼状态下的脑电信号功率值
        [h,p]=lillietest(x_i); %正态性检验
        result(i,:)=p; 
    end
    result %检验正态检验的p值

  • result =
    
        0.5000
        0.5000
        0.5000

  • p值均大于0.05，说明在显著性水平0.05下均接受原假设，即服从正态分布

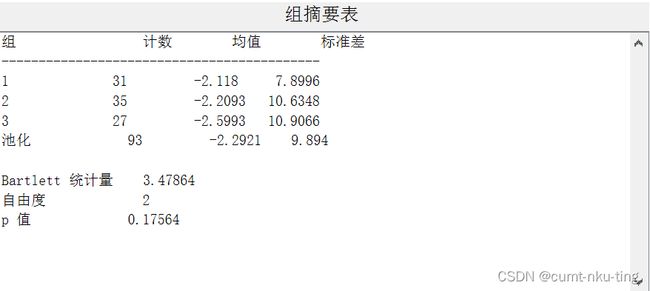
• 方差齐次性检验

  • %方差齐性检验
    [p,stats]=vartestn(x,group); %调用vartestn函数进行方差齐次性检验

  • 
  • 
  • 检验的p值=0.17564>0.05,说明在显著性水平0.05下接受原假设，认为3个时间段的脑电信号功率值服从方差相同的正态分布，满足方差分析的基本假定
• 方差分析

  • %方差分析
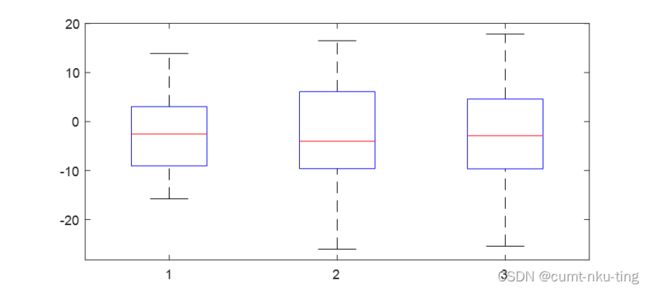
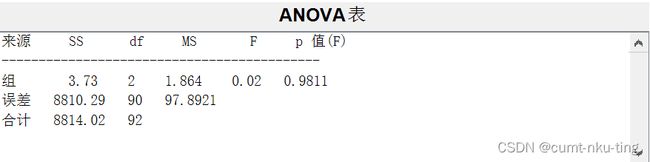
    [p,tbl,stats] = anova1(x,group);%单因素一元方差分析

  • 
  • 
• 多重比较

  • %多重比较
    [c,m,h,gnames]=multcompare(stats); %多重比较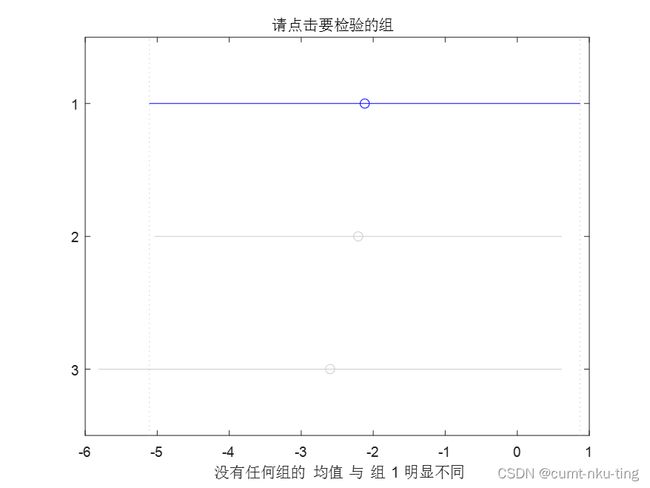

  • 
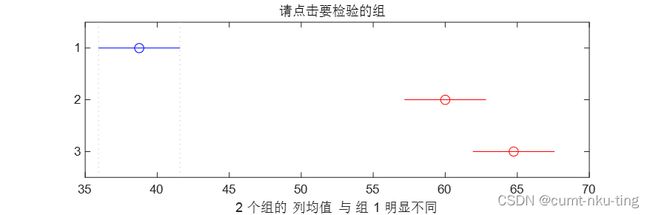
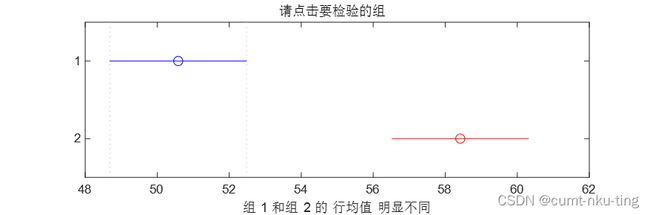
  • multcompare函数还生成一个交互式图形，可以通过鼠标单击的方式进行两两比较检验。该交互式图形上用一个符号（圆圈）标出了每一组的组均值，用一条之间段标出了每个组的组均值的置信区间。如果某两条线段不相交，即没有重叠的部分，则说明这两个组的组均值之间的差异是显著的。如果某两条直线段有重叠部分，则说明这两个组的组均值之间的差异是不显著的。可以用鼠标在图上任意选一个组，选中的组以及与选中的组差异显著的其他组均用高亮显示，选中的组用蓝色显示，与选中的组差异显著的其他组用红色显示。

  • head={'组序号','组序号','置信下限','置信上限','组均值差','p-value'};
    [head;num2cell(c)]  %将矩阵c转为元胞数组，并与head一起显示
    
    ans =
    
      4×6 cell 数组
    
        {'组序号'}    {'组序号'}    {'置信下限'}    {'置信上限'}    {'组均值差'}    {'p-value'}
        {[    1]}    {[    2]}    {[-5.7240]}    {[ 0.0913]}    {[ 5.9066]}    {[ 0.9992]}
        {[    1]}    {[    3]}    {[-5.7255]}    {[ 0.4813]}    {[ 6.6881]}    {[ 0.9814]}
        {[    2]}    {[    3]}    {[-5.6494]}    {[ 0.3900]}    {[ 6.4295]}    {[ 0.9870]}

  • head={'组序号','均值的估计值','标准误差'};
    [head;gnames num2cell(m)]  %将m转为元胞数组，和gnames一起显示
    
    ans =
    
      4×3 cell 数组
    
        {'组序号'}    {'均值的估计值'}    {'标准误差'}
        {'1'    }    {[   -2.1180]}    {[ 1.7770]}
        {'2'    }    {[   -2.2093]}    {[ 1.6724]}
        {'3'    }    {[   -2.5993]}    {[ 1.9041]}

  • 多重比较分析结果显示：p值均大于0.05，任意两组之间不存在显著差异。

2.4 单因素方差分析的MATLAB全部代码

clc;clear;close all;
[num,txt,raw] = xlsread('Resting State.xlsx');
%% one-way ANOVA
x=num(:,1);
group=num(:,4);
%正态性检验
for i=1:3
    x_i=x(group==i); %提取第i个group的睁眼状态下的脑电信号功率值
    [h,p]=lillietest(x_i); %正态性检验
    result(i,:)=p; 
end
result %检验正态检验的p值
 
%方差齐性检验
[p,stats]=vartestn(x,group); %调用vartestn函数进行方差齐次性检验
 
%方差分析
[p,tbl,stats] = anova1(x,group);%单因素一元方差分析
%多重比较
[c,m,h,gnames]=multcompare(stats); %多重比较
head={'组序号','组序号','置信下限','置信上限','组均值差','p-value'};
[head;num2cell(c)]  %将矩阵c转为元胞数组，并与head一起显示
head={'组序号','均值的估计值','标准误差'};
[head;gnames num2cell(m)]  %将m转为元胞数组，和gnames一起显示

三、双因素一元方差分析（anova2）

p=anova2(X,reps)

根据样本观测值矩阵X进行均衡实验的双因素一元方差分析。X的每一列对应因素A的一个水平，每行对应因素B的一个水平，X还应满足方差分析的基本假定。

reps表示因素A和B下的每一个水平组合下重复实验的次数。

3.1、问题

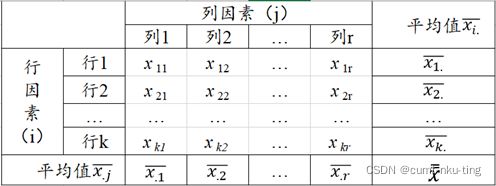
研究两个因素（行因素row和列因素column）是否对观测变量产生了显著影响。

分类： 无交互作用/有交互作用 的双因素方差分析，对于有交互作用的双因素方差分析，则需要做重复实验

3.2 步骤

• 分别对列因素和行因素提出假设

  • H0A：X的各列具有相同的均值（或因素A对实验指标的影响不显著）

  • H0B：X的各行有相同的均值（或因素B对实验指标的影响不显著）

  • A和B的交互作用不显著（注：若参数reps的取值大于1（默认值为1），anova2函数还检验因素A和因素B的交互作用是否显著）

• 统计量F值
  • 跟单因素差不多，只是行因素和列因素分别计算，可以得到两个F值
  • 
  • 

  • 无交互作用的双因素方差分析表

  • 

• 确定p值并做出统计决策

  • 根据给定的显著性水平α, 在F分布表中查找两个F值对应的相应临界值Fα，判定所检验的行因素和列因素对观察值是否有显著性差异

3.3 MATLAB代码

• 问题

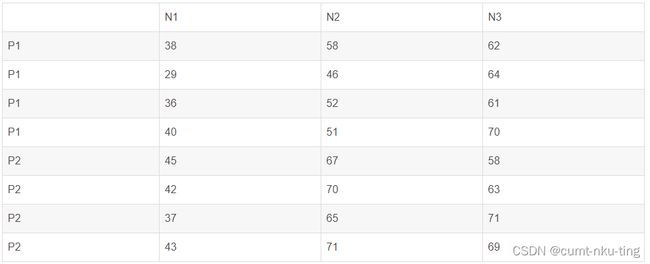
  • 为了研究肥料使用量对水稻产量的影响，某研究所做了氮（因素A）、磷（因素B）两种肥料施用量的二因素试验。氮肥用量设低、中、高三个水平，分布使用N1，N2和N3表示；磷肥用量设低、高2个水平，分别用P1，P2表示。供3x2=6个处理，重复4次，随机区组设计，测得水稻产量如下表

  • 

  •  根据上表中的数据，不考虑区组因素，分析氮、磷两种肥料的施用量对水稻产量是否有显著性影响，并分析交互作用是否显著。取显著性水平=0.05；

  • 注意：这里不需要进行正态性和方差性齐次性检验，因素数据少，在数据比较少的情况下正态检验的结果是不可靠的，即使不满足方差分析的假定，方差分析的结果通常也是比较稳定的。但是，一般情况下是必须做正态性和方差齐性检验的。

• 分析

  • 首先要把数据矩阵处理一下，要把矩阵装换成每一列对应因素A的一个水平，每行对应因素B的一个水平。本例中，每一列对应一个A因素（氮）水平，每一行对应一个B因素（磷）水平；反过来也可以。

  • 

• matlab代码
  • 双因素一元方差分析

    • % 定义一个矩阵，输入原始数据
      yield=[38 29 36 40
          45 42 37 43
          58 46 52 51
          67 70 65 71
          62 64 61 70
          58 63 71 69];
      yield=yield';  %矩阵转置
      % 将数据矩阵yield转换成8行3列的矩阵，列对应因素A（氮），行对应因素B（磷）
      yield=[yield(:,[1,3,5]);yield(:,[2,4,6])];
       
      % 定义元胞数组，以元胞数组形式显示转换后的数据
      top={'因素','N1','N2','N3'};
      left={'P1';'P1';'P1';'P1';'P2';'P2';'P2';'P2'};
       
      % 显示数据
      [top;left,num2cell(yield)];
       
      % reps表示因素A和B下的每一个水平组合下重复实验的次数
      reps=4;
       
      % 调用anova2函数作双因素方差分析，返回检验的p值向量，方差分析表，结构体标量stats
      [p,table,stats]=anova2(yield,reps)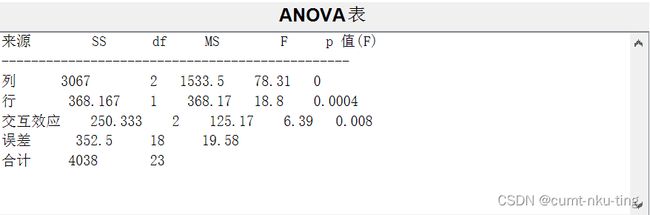

    • 

    • 因素A、因素B以及他们的交互作用对应的检验p值均小于给定的显著性水平0.05，所以可以认为氮、磷两种肥料的施用量对水稻的产量均有显著性影响，并且他们之间的交互作用也是非常显著的。由于氮、磷两种肥料的用量对水稻的产量均有非常显著的影响，可以作进一步分析，例如进行多重分析，找出因素A、B在哪种水平的组合下水稻的平均产量最高。

  • 多重比较

    • %对列（因素A）进行多重比较
      [c_A,m_A,h,gnames]=multcompare(stats,'estimate','column');
      head={'组序号','组序号','置信下限','置信上限','组均值差','p-value'};
      [head;num2cell(c_A)]  %将矩阵c转为元胞数组，并与head一起显示
      head={'组序号','均值的估计值','标准误差'};
      [head;cellstr(gnames),num2cell(m_A)]  %将m转为元胞数组，和gnames一起显示

    • 注意: 您的模型中包含一个交互效应项，它在您指定的水平非常明显。在这些条件下检验主效应是不可靠的。
      
      ans =
        4×6 cell 数组
          {'组序号'}    {'组序号'}    {'置信下限' }    {'置信上限' }    {'组均值差' }    {'p-value'   }
          {[    1]}    {[    2]}    {[-26.8971]}    {[-21.2500]}    {[-15.6029]}    {[4.9194e-08]}
          {[    1]}    {[    3]}    {[-31.6471]}    {[     -26]}    {[-20.3529]}    {[3.1051e-09]}
          {[    2]}    {[    3]}    {[-10.3971]}    {[ -4.7500]}    {[  0.8971]}    {[    0.1084]}
      
      ans =
        4×3 cell 数组
          {'组序号'}    {'均值的估计值'}    {'标准误差'}
          {'1'    }    {[   38.7500]}    {[ 1.5646]}
          {'2'    }    {[        60]}    {[ 1.5646]}
          {'3'    }    {[   64.7500]}    {[ 1.5646]}

    • 

    • %对行（因素B）进行多重比较
      [c_B,m_B,h,gnames]=multcompare(stats,'estimate','row')
      head={'组序号','组序号','置信下限','置信上限','组均值差','p-value'};
      [head;num2cell(c_B)]  %将矩阵c转为元胞数组，并与head一起显示
      head={'组序号','均值的估计值','标准误差'};
      [head;cellstr(gnames) num2cell(m_B)]  %将m转为元胞数组，和gnames一起显示

    • 注意: 您的模型中包含一个交互效应项，它在您指定的水平非常明显。在这些条件下检验主效应是不可靠的。
      
      ans =
        2×6 cell 数组
          {'组序号'}    {'组序号'}    {'置信下限' }    {'置信上限'}    {'组均值差'}    {'p-value'   }
          {[    1]}    {[    2]}    {[-11.6289]}    {[-7.8333]}    {[-4.0378]}    {[3.9813e-04]}
      
      ans =
        3×3 cell 数组
          {'组序号'}    {'均值的估计值'}    {'标准误差'}
          {'1'    }    {[   50.5833]}    {[ 1.2775]}
          {'2'    }    {[   58.4167]}    {[ 1.2775]}

    • 

四、多因素一元方差分析（anovan）

p=anovan(y,group)

4.1、问题

• 为了研究肥料使用量对水稻产量的影响，某研究所做了氮（因素A）、磷（因素B）两种肥料施用量的二因素试验。氮肥用量设低、中、高三个水平，分布使用N1，N2和N3表示；磷肥用量设低、高2个水平，分别用P1，P2表示。供3x2=6个处理，重复4次，随机区组设计，测得水稻产量如下表
• 
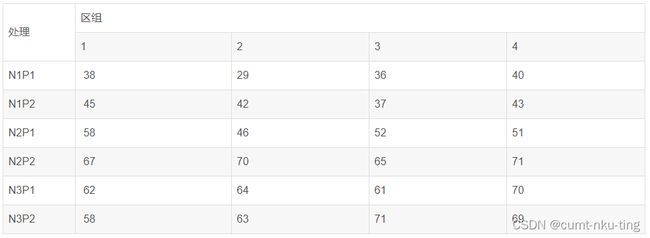
• 根据上表中的数据，分析氮、磷哪种组合对水稻产量是否有显著性影响。取显著性水平=0.05；

4.2 MATLAB代码

• 多因素一元方差分析

  • % 定义一个矩阵，输入原始数据
    yield=[38 29 36 40
        45 42 37 43
        58 46 52 51
        67 70 65 71
        62 64 61 70
        58 63 71 69];
    yield=yield'  % 矩阵转置
    % 将数据矩阵yield按列拉长成24行1列的向量
    yield=yield(:);
    % 定义因素A(氮)的水平列表向量
    A=strcat({'N'},num2str([ones(8,1);2*ones(8,1);3*ones(8,1)]));
     
    % 定义因素B(磷)的水平列表向量
    B=strcat({'P'},num2str([ones(4,1);2*ones(4,1)]));
    B=[B;B;B];
     
    % 将因素A、B的水平列表向量与yield向量放在一起构成一个元胞数组，以元胞数组形式显示出来
    [A,B,num2cell(yield)]
     
    % 指定因素名称，A表示氮肥施用量，B表示磷肥施用量
    varnames={'A','B'};
     
    % 调用anovan函数作双因素一元方差分析，返回主效应A、B和交互效应AB所对应的p值向量
    % 还返回方差分析表table，结构体变量stats，标识模型效应项的矩阵term
    [p,table,stats,term]=anovan(yield,{A,B},'model','full','varnames',varnames)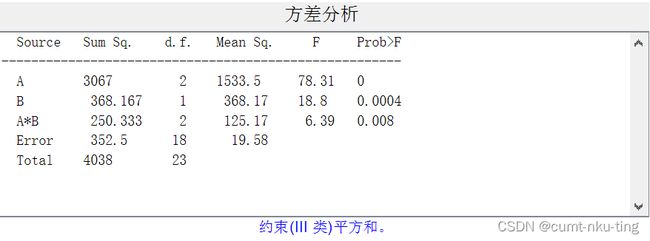

  • 
• 多重比较

  • %多重比较
    [c,m,h,gnames]=multcompare(stats,'dimension',[1 2])
     
    %查看各处理的均值
    [gnames,num2cell(m)]

  • ans =
      16×6 cell 数组
        {'组序号'}    {'组序号'}    {'置信下限' }    {'置信上限' }    {'组均值差' }    {'p-value'   }
        {[    1]}    {[    2]}    {[-25.9446]}    {[-16.0000]}    {[ -6.0554]}    {[8.7776e-04]}
        {[    1]}    {[    3]}    {[-38.4446]}    {[-28.5000]}    {[-18.5554]}    {[5.1236e-07]}
        {[    1]}    {[    4]}    {[-15.9446]}    {[      -6]}    {[  3.9446]}    {[    0.4236]}
        {[    1]}    {[    5]}    {[-42.4446]}    {[-32.5000]}    {[-22.5554]}    {[8.7653e-08]}
        {[    1]}    {[    6]}    {[-39.4446]}    {[-29.5000]}    {[-19.5554]}    {[3.1431e-07]}
        {[    2]}    {[    3]}    {[-22.4446]}    {[-12.5000]}    {[ -2.5554]}    {[    0.0093]}
        {[    2]}    {[    4]}    {[  0.0554]}    {[ 10.0000]}    {[ 19.9446]}    {[    0.0483]}
        {[    2]}    {[    5]}    {[-26.4446]}    {[-16.5000]}    {[ -6.5554]}    {[6.2868e-04]}
        {[    2]}    {[    6]}    {[-23.4446]}    {[-13.5000]}    {[ -3.5554]}    {[    0.0047]}
        {[    3]}    {[    4]}    {[ 12.5554]}    {[ 22.5000]}    {[ 32.4446]}    {[1.4062e-05]}
        {[    3]}    {[    5]}    {[-13.9446]}    {[ -4.0000]}    {[  5.9446]}    {[    0.7926]}
        {[    3]}    {[    6]}    {[-10.9446]}    {[      -1]}    {[  8.9446]}    {[    0.9995]}
        {[    4]}    {[    5]}    {[-36.4446]}    {[-26.5000]}    {[-16.5554]}    {[1.4498e-06]}
        {[    4]}    {[    6]}    {[-33.4446]}    {[-23.5000]}    {[-13.5554]}    {[7.8003e-06]}
        {[    5]}    {[    6]}    {[ -6.9446]}    {[  3.0000]}    {[ 12.9446]}    {[    0.9251]}
    
    ans =
      7×3 cell 数组
        {'组序号'    }    {'均值的估计值'}    {'标准误差'}
        {'A=N1,B=P1'}    {[   35.7500]}    {[ 2.2127]}
        {'A=N2,B=P1'}    {[   51.7500]}    {[ 2.2127]}
        {'A=N3,B=P1'}    {[   64.2500]}    {[ 2.2127]}
        {'A=N1,B=P2'}    {[   41.7500]}    {[ 2.2127]}
        {'A=N2,B=P2'}    {[   68.2500]}    {[ 2.2127]}
        {'A=N3,B=P2'}    {[   65.2500]}    {[ 2.2127]}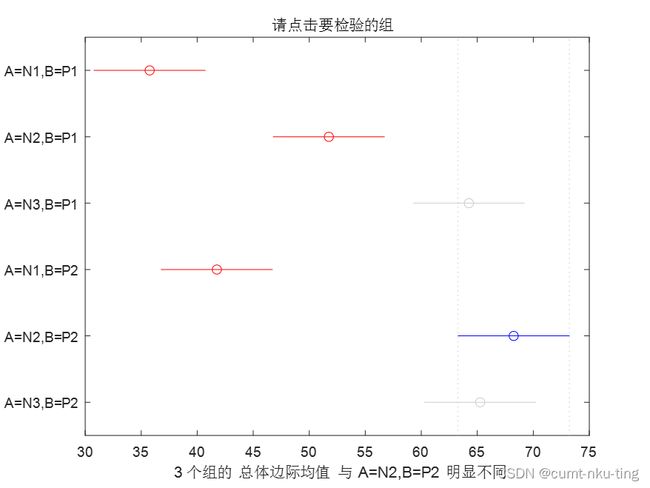

  • 

  • 返回的矩阵c是6种处理（N1P1，N2P1，N3P1，N1P2，N2P2，N3P2）间多重比较的结果矩阵，每一行的前两列是进行比较的两个处理的编号，第4列是两个处理的均值之差，第3列是两个处理均值差的95%置信下限，第5列是两个处理均值差的95%置信下限，当两个处理均值差的95%置信区间不包含0时，说明在显著性水平0.05下，这两个处理均值间差异是显著的。m矩阵列出了6种处理的平均值，很明显第5个处理（即N2P2）的平均值最大，由矩阵c或交互式多重比较的图中可以得到，处理5与处理3,6差异不显著，所以可以认为第3个和第6个处理也是可以的，所以，综上，可以在处理3,5,6中做出选择，即N3P1，N2P2，N3P2。