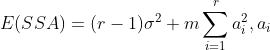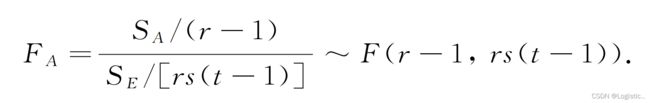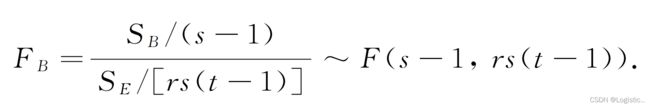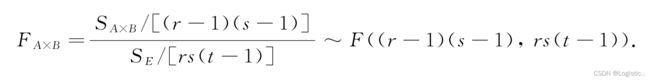方差分析基本介绍以及MATLAB实现

在实际间题中，影响一个事物的因素是很多的，人们总是希望通过各种试验来观察各种因素对试验结果的影响.例如，不同的生产厂家，不同的原材料、不同的操作规程以及不同的技术指标对产品的质量、性能都会有影响.然而，不同因素的影响大小不等

方差分析(analysis of variance.，ANOVA)是研究一种或多种因素的变化对试验结果的观测值是否有影响，从而找出较优的试验条件或生产条件的一种常用的统计方法

人们在试验中所考察到的数量指标，如产量、性能等，称为观测值，影响观测值的条件称为因素，因素的不同状态称为水平，在一个试验中，可以得出一系列不同的观测值。引起观测值不同的原因是多方面的，有的是处理方式或条件不同引起的，这些称为因素效应（或处理效应、条件变异）：有的是试验过程中偶然性因素的干扰或观测误差所导致的，这些称为试验误差。

方差分析的主要工作是将测量数据的总变异按照变异原因的不同分解为因素效应和试验误差，并对其作出数量分析，比较各种原因在总变异中所占的重要程度，作出统计推断的依据，由此确定进一步的工作方向

单因素方差分析

对于一般情况下，设试验只有一个因素A在变化，其他因素都不变。A有r个水平，在水平下进行次独立观测，设表示在因素的第个水平下的第次试验的结果，得到试验指标列在下表中，

简单地说：方差分析的研究内容是单因素/多因素影响下，多个正态总体的均值是否有显著差异，以及影响因素是否显著。

具体的过程是先构造检验统计量，求解出p值，和显著性水平相比较，若p值小于显著性水平，那我们拒绝原假设，任务这个因素显著。

p值：利用样本观测值得到的能够拒绝原假设的最小显著性水平

数学模型：

因子有个水平，所以我们有个总体，假定：

(1).每个总体均为正态性总体，记为

(2).

(3).每个总体中抽取的样本相互独立，即之间相互独立

方差分析的工作是进行一个假设检验，原假设

不全相等

成立时，因子的个水平均值相同，对总体的影响不显著，否则，因子对总体的影响显著

构造检验统计量：我们利用平方和分解和均方构造的检验统计量，下面是比较简易的过程

总离差平方和(SST)：

SST=SSA+SSE

下面引入均方，均方就是平方和与对应的自由度之比

下面我们不加证明的三个引理

1. 
2. 的定义在下面
3. SSA,SSE独立

之间相互独立,

的拒绝域:

 单因素方差分析表

若认为因素A显著

若,认为因素A不显著

下面是一个单因素方差分析的例题，选自《概率论与数理统计教程》茆诗松第三版

例1：为研究咖啡因对人体功能的影响，随机选择30名体质大致相同的健康男大学生进行手指叩击训练，此外咖啡因选三个水平：:

每个水平下冲泡10杯水，外观无差别，并加以编号，然后让30名大学生每人从中任选一杯服下，2小时后，请每人做手指叩击，统计员记录其每分钟叩击次数，试验结果统计如下表：

咖啡因剂量	叩击次数
A:0mg	242	245	244	248	247	248	242	244	246	242
A:100 mg	248	246	245	247	248	250	247	246	243	244
A:200 mg	246	248	250	252	248	250	246	248	245	250

 请对上述数据进行方差分析

单因素方差分析

perminute=[242	245	244	248	247	248	242	244	246	242
248	246	245	247	248	250	247	246	243	244
246	248	250	252	248	250	246	248	245	250];
p=anova1(perminute');

 p值为0.0062，可以说在0.01的显著性水平下，该因素的影响是显著性的

 

在许多实际问题中, 需要考虑影响试验数据的因素多于一个的情形． 例如, 在

化学试验中, 几种原料的用量、反应时间、温度的控制等都可能影响试验结果, 这就

构成了多因素试验问题。

设有A,B两个因素,因素A有r个水平A_1 , A_2 , \dots, A_r ,因素B 有s 个水平

B_1, B_2, \dots, B_s.

不考虑交互作用

因素A,B的每一个水平组合(A_i,B_j)下进行一次独立试验得到观测值x_{ij}(i＝1,2,\dots,r;j＝1,2,\dots,s).观测数据见下表

	B_1	B_2	\dots	B_s
A_1	x_{11}	x_{11}	\dots	x_{11}
A_2	x_{11}	x_{11}	\dots	x_{11}
\dots	\dots	\dots	\dots	\dots
A_r	x_{11}	x_{11}	\dots	x_{11}

假定且各x_{ij}相互独立,不

考虑两因素的交互作用, 因此模型可以归结为

之间相互独立,

其中，为总平均；

为因素A第i个水平的效应;为因素B第j个水平的效应.

在上面的线性模型下, 方差分析的主要任务是系统分析因素A和因素B对试

验指标影响的大小。因此,在给定显著性水平下, 提出以下统计假设：

对于因素A , “因素A对试验指标影响不显著”等价于

对于因素B , “因素B 对试验指标影响不显著”等价于

．

双因素方差分析与单因素方差分析的统计原理基本相同, 也是基于平方和分

解公式

SST＝SSE＋SSA＋SSB,

其中,

S_T为总离差平方和, S_E为误差平方和, S_A 为由因素A的不同水平所引起的

离差平方和(称为因素A的平方和).类似地, S_B 称为因素B的平方和.可以证明,

当H_{01}成立时

且与S_E相互独立,而

于是当H_{01}成立时,

类似地, 当H_{02}成立时,

分别以F_A 和F_B 作为H_{01}和H_{02}的检验统计量, 把计算结果列成方差分析

表, 见表

考虑交互作用

设有A,B两个因素,因素A有r个水平A_1, A_2,\dots,A_r,因素B有s个水平B_1,B_2,\dots, B_s.每一个水平组合(A_i,B_j ) 下重复试验t次,记录第k次的观测值

为x_{ijk} , 把观测数据列表, 见表

假定且各x_{ijk}相互独立,不因此模型可以归结为

之间相互独立,

其中，是因素A第i个水平的效应，是因素B第j个水平的效应，是A_i和B_j的交互效应，因此有

此时,判断因素A,B交互效应的影响是否显著等价于下列检验假设：

在这种情况下, 方差分析法与前面的方法类似,有以下计算公式：

其中

为总离差平方和, 为误差平方和, 为由因素A的平方和, 称为B

的平方和, 交互平方和.可以证明,当成立时,

当成立时，

当成立时，

分别以作为的检验统计量,把检验结果列成

方差分析表, 见下表

 

例2

设有如下表所列的3个组5个保险理赔额的观测数据，请用方差分析法检验3个组的理赔额是否有显著性差异（F_{0.05}(2,12)=4.6）

	i=1	i=2	t=3	I=4	t=5
j=l	98	93	103	92	110
j=2	100	108	118	99	111
j=3	129	140	108	105	116

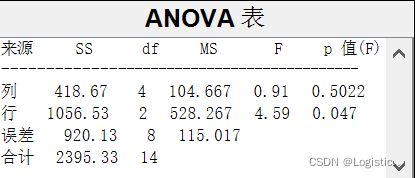
保险理赔额观测数据的方差分析

databx=[98	93	103	92	110;
100	108	118	99	111;
129	140	108	105	116];
p=anova2(databx);

结果解释：行的p值位0.047<0.05，所以在显著性水平0.05的情况下认为行因素显著，列因素不显著，即j=1,j=2,j=3显著影响保险理赔额，t没有显著影响保险理赔额。

例3

老鼠存活时间方差分析

有一个关于检验毒药强弱的实验，给48只老鼠注射I，Ⅱ，II三种毒药（因素A)，同时有A，B，C和D四种治疗方案（因素B)，这样的试验在每一种因素组合下都重复四次测试老鼠的存活时间，数据见下表，试分析毒药和治疗方案以及它们的交互作用对老鼠存活时间有无显著影响.

	A		B		C		D
1	0.31	0.45	0.82	1.1	0.43	0.45	0.45	0.71
	0.46	0.43	0.88	0.72	0.63	0.76	0.66	0.62
11	0.36	0.29	0.92	0.61	0.44	0.35	0.56	1.02
	0.4	0.23	0.49	1.24	0.31	0.4	0.71	0.38
11	0.22	0.21	0.3	0.37	0.23	0.25	0.3	0.36
	0.18	0.23	0.38	0.29	0.24	0.22	0.31	0.33

 

time=[0.310000000000000	0.450000000000000	0.820000000000000	1.10000000000000	0.430000000000000	0.450000000000000	0.450000000000000	0.710000000000000
0.460000000000000	0.430000000000000	0.880000000000000	0.720000000000000	0.630000000000000	0.760000000000000	0.660000000000000	0.620000000000000
0.360000000000000	0.290000000000000	0.920000000000000	0.610000000000000	0.440000000000000	0.350000000000000	0.560000000000000	1.02000000000000
0.400000000000000	0.230000000000000	0.490000000000000	1.24000000000000	0.310000000000000	0.400000000000000	0.710000000000000	0.380000000000000
0.220000000000000	0.210000000000000	0.300000000000000	0.370000000000000	0.230000000000000	0.250000000000000	0.300000000000000	0.360000000000000
0.180000000000000	0.230000000000000	0.380000000000000	0.290000000000000	0.240000000000000	0.220000000000000	0.310000000000000	0.330000000000000];

time_clean=zeros(3,16);
for i=1:3
    for j=1:4
        time_clean(i,4*j-3)=time(2*i-1,2*j-1);
        time_clean(i,4*j-2)=time(2*i-1,2*j);
        time_clean(i,4*j-1)=time(2*i,2*j-1);
        time_clean(i,4*j)=time(2*i,2*j);
    end
end
time_clean=time_clean';
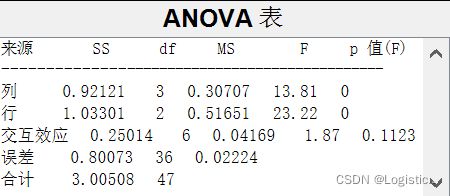
p=anova2(time_clean,4);

双因素有交互方差分析 

 

结果解释：列和行的p值都接近于0，交互效应的p值大于0.05，行因素毒药种类（I,II,III）对老鼠寿命的影响是显著的，列因素治疗方案（A,B,C,D）对老鼠寿命的影响是显著的，两者的交互影响不显著。