DataWhale 9月组队学习-动手学数据分析 task3_学习记录
建模
数据分析我认为最重要的部分就是运用我们目前已有的数据建立模型,对未知的东西进行一个预测。当然数据本身也是非常重要的,所以需要前面的增删查补,对数据进行一个规整,以此可以训练出一个健壮的模型。
首先是导入包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import Image
前面三个库是老朋友了,就不做过多的介绍了。
- seaborn
seaborn和matplotlib一样是一个数据可视化的库,但不一样的地方在于seaborn是在matplotlib的基础上及逆行了更高级的API封装,可以通过更少的代码去调用matplotlib的方法,而且它的默认绘图风格和色彩搭配都更具吸引力,不是说matplotlib不行,matplotlib可以制作具有更多特色的图。
- IPython.display.Image
不好意思暂时没搞懂用来干嘛的哈哈哈,没看明白。 网页链接:Module: display — IPython 3.2.1 documentation
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.rcParams['figure.figsize'] = (10, 6) # 设置输出图片大小
通常matplotlib制作图标标题时,最容易遇到中文字符乱码的问题,在输出图表之前写入plt.rcParams['font.sans-serif'] = ['SimHei']代码,可以避免这个问题。例如:
加代码前:
加代码后:
切割训练集和测试集
训练模型时,通常不会将所有的数据一股脑丢进去进行训练,否则训练出来的结果我们没有办法去估量它到底是不是一个良好的模型,所以我们需要保留一部分的数据,用于测试或者验证,看看模型有没有举一反三的能力,如果训练出来的模型只能用于当前数据,而对新数据无法进行预测,那么这个模型将意义不大。一般的数据集会被分为:训练集、验证集和测试集。
- 训练集:训练集的数据都是用于训练模型的参数
- 验证集:验证集的数据是用于对模型的参数进行调优,并初步评估模型是否正确
- 测试集:测试集的数据用于测试模型的泛化能力,以”未知的数据“这个身份进行测试,以此来确定最终模型
但在一般的模型里,用的较多的就是训练集和测试集,而没有验证集,这个先不说。
对数据集进行切割时,最常见的比例就是7:3和8:2(训练集:测试集),吴恩达老师说过:80%的数据+20%的模型=更好的机器学习,当然不一定只能遵守”二八定律“,学习者应该根据具体数据进行人为的判断,尝试更多切割比例来找到一个对模型训练最优的。(不过我觉得训练集必须得比测试集多,没试过”以小博大“)
载入数据
# 读取原数据数集
train = pd.read_csv('train.csv')
#读取清洗过的数据集
data = pd.read_csv('clear_data.csv')
X = data
y = train['Survived']
这里原数据和清洗过的数据基本上是一样的,只不过清洗过的数据少了”Survived“,所以清洗过的数据我们将它作为特征,而原数据里的"Survived"作为标签。
导入切割数据集的库
from sklearn.model_selection import train_test_split
train_test_split语法:
X_train,X_test, y_train, y_test =cross_validation.train_test_split(X,y,test_size, random_state)
参数说明:
- X:待划分的样本特征集合
- y:待划分的样本标签
- test_size: 若在0~1之间,为测试集样本数目与原始样本数目之比;若为整数,则是测试集样本的数目。
- random_state:随机数种子
- X_train:划分出的训练集数据(返回值)
- X_test:划分出的测试集数据(返回值)
- y_train:划分出的训练集标签(返回值)
- y_test:划分出的测试集标签(返回值)
- shuffle:是否打乱数据的顺序,再划分,默认True
- stratify:none或者array/series类型的数据,表示按这列进行分层采样
train_test_split()可以对数据集进行随机分组,设置的随机种子数不同,最后分组后的数据也就不同,通常为了保证代码的可复现,随机种子数一般保持不变。stratify参数默认为none,可以选择根据某列来进行分层抽样。
创建模型
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
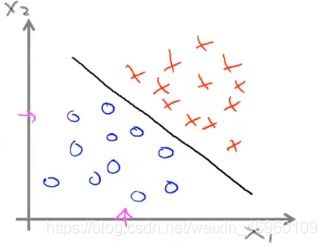
逻辑回归模型是经典的分类模型,并不是回归模型。如下图所示,算法会通过大量的数据训练,拟合出一条可以将两种不同的标签分离开来的直线,这大概就是逻辑回归的大致思路。
# 默认参数逻辑回归模型
lr = LogisticRegression()
训练模型
# 开始训练
lr.fit(X_train, y_train)
# 查看训练集和测试集score值
print("Training set score: {:.2f}".format(lr.score(X_train, y_train)))
print("Testing set score: {:.2f}".format(lr.score(X_test, y_test)))
# 输出结果
Training set score: 0.80
Testing set score: 0.79
参数调整
首次跑通模型时,常常需要进一步对模型的参数进行修改,以便寻找出良好的模型
# 调整参数后的逻辑回归模型
lr2 = LogisticRegression(C=100)
lr2.fit(X_train, y_train)
# 查看训练集和测试集score值
print("Training set score: {:.2f}".format(lr2.score(X_train, y_train)))
print("Testing set score: {:.2f}".format(lr2.score(X_test, y_test)))
# 输出结果
Training set score: 0.79
Testing set score: 0.78
可以看到通过修改传入的参数值,模型最终的得分也发生了改变,当然这里是反向上分。
数学关系
首先以二分类为例,对于所给数据集假设存在一条直线可以将数据完成线性可分。那么该决策边界将其表示为:
![]()
当给定数据集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) , y i ∈ 0 , 1 , i = 1 , 2 , . . . , n D = (x_1,y_1),(x_2,y_2),...,(x_n,y_n),y_i∈0,1,i=1,2,...,n D=(x1,y1),(x2,y2),...,(xn,yn),yi∈0,1,i=1,2,...,n所得的 z = w T x + b z=w^Tx+b z=wTx+b的取值为R,不符合值域{0,1},所以需要一个阶跃函数将实数z映射到(0,1)之间。
因为Sigmoid函数连续可求导的,所以使用Sigmoid函数将实数z进行映射,其表达式为: S ( z ) = 1 1 + e − z S(z)=\frac{1}{1+e^{-z}} S(z)=1+e−z1。

确定好数学形式之后,接下来可使用代价函数来求解数学模型中的参数 w w w和 b b b,也就拟合出了Logistic回归模型的最佳参数,这一段初学者可以参考 吴恩达的机器学习课程 。
预测结果
预测理论上是数据分析的最后一步,其实并不是,因为这里还有一个循环,从预测得出的结果还得向前面进行反馈,当预测结果十分不尽人意的时候,这个时候需要重新对数据、预处理以及参数进行审查,是否出现了遗漏的问题或者是处理不当。
# 预测标签
pred = lr.predict(X_train)
# 此时我们可以看到0和1的数组
pred[:10]
# 输出结果
array([0, 1, 1, 1, 0, 0, 1, 0, 1, 1])
这里将结果的前十个数据进行了展示,可以看到最终的结果就是0和1,这是通过激活函数得出的,原始的是[0,1]之间的小数,通过指定一个阈值将结果二值化,得到上面的0和1结果。
# 预测标签概率
pred_proba = lr.predict_proba(X_train)
pred_proba[:10]
# 输出结果
array([[0.60870022, 0.39129978],
[0.17725433, 0.82274567],
[0.40750365, 0.59249635],
[0.18925851, 0.81074149],
[0.87973912, 0.12026088],
[0.91374559, 0.08625441],
[0.13293198, 0.86706802],
[0.90560801, 0.09439199],
[0.05283987, 0.94716013],
[0.10936016, 0.89063984]])
[0.87973912, 0.12026088],
[0.91374559, 0.08625441],
[0.13293198, 0.86706802],
[0.90560801, 0.09439199],
[0.05283987, 0.94716013],
[0.10936016, 0.89063984]])
模型评估
模型评估是指用评价函数(metrics)来评估模型的好坏,可作为在训练中调整超参数、评估模型效果的重要依据。不同类型的模型任务会选取不同评价函数,常见的如回归类任务会用均方差(MSE),二分类任务会用AUC (Area Under Curve)值等。
评价函数和loss函数非常相似,但不会参与模型的训练优化。
评价函数的输入为模型的预测值(preds)和标注值(labels),并返回计算后的评价指标。
分类模型
正负样本
- 正样本:需要判定概率为1的类型的样本叫做正样本
- 负样本:需要判定概率为0的类型的样本叫做负样本
对于二分类问题,按照真实类别和分类器预测类别划分为:
真正例(True Positive,TP):真实类别为正例,预测类别为正例。
假正例(False Positive,FP):真实类别为负例,预测类别为正例。
假负例(False Negative,FN):真实类别为正例,预测类别为负例。
真负例(True Negative,TN):真实类别为负例,预测类别为负例。
由这四个部分可以构建一个混淆矩阵,如下:
常见的评估指标
- 准确率(Accuracy)
- 精准率(Precision)
- 召回率(Recall)
- P-R曲线(Precision-Recall)
- F1 score
- ROC曲线
准确率(Accuracy)
准确率就是分类正确的样本占总样本个数的比例。
就像是考试写判断题,一共10道题,只写对了5道,那准确率就是50%。
公式:
A C C = T P + T N T P + T N + F P + F N ACC=\frac{TP+TN}{TP+TN+FP+FN} ACC=TP+TN+FP+FNTP+TN
这个是最简单的也是现实生活中最常用的分类指标,但是用与模型的评估的时候,就并不是那么的准确。就比如说10道选择题,正确答案全是“否”,我不会我乱蒙,全蒙“否”,那我就是准确率100
%,那这个准确率并不能反映出我这段时间的学习水平,大概就是这个意思。所以准确率这个指标对数据占比有一定的要求,不能随便乱用。
精准率(Precision)
也叫查准率,是指分类正确的正样本个数占分类器判定为正样本的样本个数的比例。
就像是10道选择题,我判断了6题为“是”,但这6个中只有3个正确答案是“是”,那此时我的精准率就是50%。
公式:
P = T P T P + F P P=\frac{TP}{TP+FP} P=TP+FPTP
召回率(Recall)
也称为查全率。是指分类正确的正样本个数占真正的正样本个数的比例。
相对于精准率,其实就是分母不同,一个分母是预测为正的样本数,另一个是原来样本中所有的正样本数。还是那个例子,10道选择题,其中有6个正确答案为“是”,但这6道题我只有3道拿到了分,那召回率就是50%。
公式:
P = T P T P + F N P=\frac{TP}{TP+FN} P=TP+FNTP
精准率和召回率是我看了最久的两个指标,越看越理不清,本来想单独举个例子来理解的,发现举的例子都并不准确,尤其是精准率,不知道应该单独运用在什么事例里;但是召回率就比较好理解,像是预测新冠肺炎的病人,像是预测特斯拉有问题的车这些用召回率都挺好理解的,把有问题的尽可能的揪出来。
参考链接:https://blog.csdn.net/edogawachia/article/details/79307509
P-R曲线(Precision-Recall)
P-R曲线的横轴是召回率,纵轴是精确率。对于一个排序模型来说,其P-R曲线上的一个点代表着,在某一阈值下,模型将大于该阈值的结果判定为正样本,小于该阈值的结果判定为负样本,此时返回结果对应的召回率和精确率。

算法对样本进行分类时,一般都会有置信度,即表示该样本是正样本的概率,比如99%的概率认为样本A是正例,1%的概率认为样本B是正例。通过选择合适的阈值,比如50%,对样本进行划分,概率大于50%的就认为是正例,小于50%的就是负例。
通过置信度就可以对所有样本进行排序,再逐个样本的选择阈值,在该样本之前的都属于正例,该样本之后的都属于负例。每一个样本作为划分阈值时,都可以计算对应的precision和recall,那么就可以以此绘制曲线。
参考链接:https://blog.csdn.net/b876144622/article/details/80009867
F1 score
是精准率和召回率的调和平均值,它定义为:
F 1 = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l F1=\frac{2×Precision×Recall}{Precision+Recall} F1=Precision+Recall2×Precision×Recall
用调和平均而不是简单的算术平均的原因是:调和平均可以惩罚极端情况。一个具有 1.0 的精度,而召回率为 0 的分类器,这两个指标的算术平均是 0.5,但是 F1 score 会是 0。F1 score 给了精度和召回率相同的权重,它是通用 Fβ指标的一个特殊情况,在 Fβ中,β 可以用来给召回率和精度更多或者更少的权重。
参考链接:https://www.jianshu.com/p/1afbda3a04ab