Ant Colony Optimization蚁群优化算法(ACO算法)概念及实战
Ant Colony Optimization
蚁群优化算法(ACO算法)
定义
蚁群算法(ant colony optimization, ACO),又称蚂蚁算法,是一种用来寻找优化路径的机率型算法。它由Marco Dorigo于1992年在他的博士论文中提出,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。
算法思想
- 相互协作的一群蚂蚁可以战胜比自己强壮的昆虫,并把它搬回巢;而单个蚂蚁则不能。
- 此外,蚂蚁还能够适应环境的变化,例如在蚁群的运动路线上突然出现障碍物时,它们能够很快地重新找到最优路径。
昆虫学家通过大量研究发现:蚂蚁个体之间是通过信息交流来找到从蚁巢到食物源的最短路径的
- 蚂蚁个体通过在其所经过的路上留下一种称之为“信息素”(pheromone)或“迹”的物质来实现与同伴之间的信息传递。
- 随后的蚂蚁遇到信息素时,不仅能检测出该物质的存在以及量的多少,而且可根据信息素的浓度来指导自己对前进方向的选择。
基本原理
蚁群算法的基本原理如下
- 蚂蚁在路径上释放信息素
- 碰到还没走过的路口,就随机挑选一条路走,同时,释放与路径长度有关的信息素
- 信息素浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时,就有大概率选择信息素浓度较高的路径
- 最优路径上的信息素浓度越来越大
- 最终蚁群找到最优寻食路径
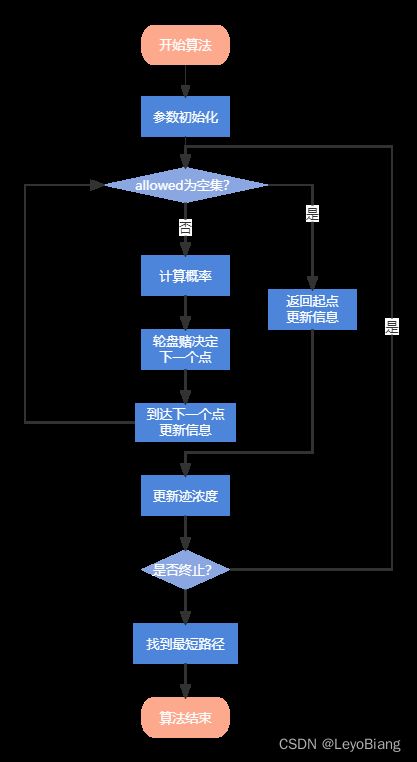
算法流程
我们将在例题中仔细介绍这一步步的流程,比如参数初始化时需要初始化什么参数,上图中的allowed是什么内容等等等等
例题
我们以旅行商问题(Traveling Salesman Problem TSP)为例,这里给不太了解什么是旅行商问题的同学解释一下什么是TSP问题
TSP问题:
给定n个城市,m条路径(无向边)连接这n个城市,每条路径(无向边)有一个权值代表两个城市之间的距离,现在要求旅行商把每一个城市都走一遍并回到原点,求路径的最短值。
在我们具体问题中 ,我们给定4个城市,每个城市之间都有一条路径(无向边),路径长度矩阵如下:
[ 0 2 6 3 2 0 4 1 6 4 0 8 3 1 8 0 ] \left[ \begin{array}{ll} 0 & 2 & 6 & 3\\ 2 & 0 & 4 & 1\\ 6 & 4 & 0 & 8\\ 3 & 1 & 8 & 0 \end{array} \right] ⎣ ⎡0263204164083180⎦ ⎤
参数初始化
我们假设旅行商(蚂蚁)数量m为2,城市数量n为4,城市i和城市j之间的距离为d[i][j] (i,j=1,2,…,n)
# 蚂蚁数
m = 2
# 城市数
n = 4
# 生成一张图
d = np.array([[0,2,6,3],
[2,0,4,1],
[6,4,0,8],
[3,1,8,0]])
我们更新信息素浓度时需要一个常数Q(这个后面会提到);并且我们知道信息素在现实中是会随着时间挥发的,所以我们需要设定挥发率ρ;我们还要给每条路径上都设置一个基础的信息素浓度τ_0;以及初始化一个存储每条路径的信息素的一个二维数组τ
Q = 10
# 挥发率
rho = 0.5
#初始信息素浓度
tau_0 = 0.4
#初始化信息素浓度
tau = np.ones((n,n))*tau_0
# 自己到自己的信息素为0
for index in range(n):
tau[index][index]=0
这里我们需要注意,不管是d还是τ,这两个二维数组都应当是对称矩阵,因为同一条路径不管是从i到j还是从j到i,一般情况下都是距离一样的,而且信息素浓度也应当一样。(除非有特殊情况,比如由于地形原因导致的路程不同等等,但是在这里我们不做考虑)
迭代
迭代之前我们需要确定终止的条件,在这里我们选用了迭代次数上限作为条件
我们为了记录迭代的变化,我们记录了每一轮迭代的得到的旅行商最短长度以及对应的路径
# 迭代次数
n_epoch = 2
# 记录每一轮迭代的最短长度
shortest_path_L_record = np.zeros(n_epoch)
# 记录每一轮迭代的最短长度的路径
shortest_path_record = np.zeros(shape=(n_epoch,n+1))
for epoch in range(n_epoch):
# 迭代内容
在迭代前其实还需要一次参数的初始化,不过初始化的将是迭代时才需要的参数
迭代参数初始化
我们知道旅行商(蚂蚁)们是通过信息素得到概率加上轮盘赌来决定往哪里走的,这里我们可以记录下他们的概率p,(这个也可以不记录的,直接用临时变量做计算即可)
allowed是用来记录旅行商(蚂蚁)们当前可以往哪个城市(点)移动
current_cities 是用来记录旅行商(蚂蚁)们当前的位置,在一开始我们需要让他们随机分布在各个城市(点)
由于我们在旅行的最后需要返回起点,所以我们需要记录下起点的位置,于是便有了start_cities
在后面我们更新迹浓度时我们需要用到旅行商(蚂蚁)们每一次的移动的路线,于是我们有了move,其中move[i][j][k]的值代表第k个旅行商(蚂蚁)是否从城市(点)i移动到城市(点)j过
由于在这里我们示范的算法是ant-cycle蚁群算法,所以在后面更新迹浓度时还需要用到旅行商(蚂蚁)走过的总路程L
# 记录第k只蚂蚁从i往j走的概率
p = np.zeros(shape=(m,n,n))
# 记录第k只蚂蚁可以往哪个城市移动
allowed = np.ones(shape=(m,n))
# 记录第k只蚂蚁当前所在的城市的array 初始化时让他们处于随机城市
current_cities = np.array(np.floor(np.random.random(m)*n),dtype=np.int)
# 记录第k只蚂蚁出发的城市
start_cities = current_cities.copy()
# 我们需要记录每一次的移动的路径 (后面迹更新机制要用到)
move = np.zeros(shape=(n,n,m),dtype=np.int)
# 在allowed中把当前所在的城市设置为不可去 即值为0
for index in range(m):
first_city = int(current_cities[index])
allowed[index][first_city]=0
# L代表的是这个蚂蚁走过的总长度 如果对于下面这个L的用处有疑惑 我建议可以继续往下看
L = np.zeros(shape=(m))
# 用于记录当前时刻
t=0
判断allowed是否为空集
如前面所说,allowed是用来记录旅行商(蚂蚁)们当前可以往哪个城市(点)移动的集合,但是我们的实现采用的是数组
allowed = np.ones(shape=(m,n))
当allowed[k][j]=1则说明,第k个旅行商(蚂蚁)还被允许往城市(点)j移动,
当allowed[k][j]=1则说明,第k个旅行商(蚂蚁)不被允许往城市(点)j移动。
按照这个思路,也就是allowed[k]的值全部为0,就说明第k个旅行商(蚂蚁)已经没地方可以去了
所以我们使用以下代码来实现对这个问题的判断
while allowed.max()!=0:
计算概率
当前旅行商(蚂蚁)在城市(点)i,假设只考虑信息素浓度对蚂蚁选择路径的影响:
P i j k ( t ) = { τ i j ( t ) ∑ s ∈ a l l o w e d k τ i s ( t ) , j ∈ a l l o w e d k 0 , j ∉ a l l o w e d k P_{ij}^k(t)= \left \{ \begin{array}{ll} \frac{\tau_{ij}(t)}{\sum_{s\in allowed_k}\tau_{is}(t)}, & j\in allowed_k\\ 0, & j\notin allowed_k \end{array} \right. Pijk(t)={∑s∈allowedkτis(t)τij(t),0,j∈allowedkj∈/allowedk
- p[k][i][j] : t时刻第k只蚂蚁从点i转移到点ij的概率
- s : 暂未访问的点i集合(allowed)中的某一个点i
由于
∑ s ∈ a l l o w e d k τ i s ( t ) \sum_{s\in allowed_k}\tau_{is}(t) s∈allowedk∑τis(t)
在一轮迭代中对于在同一个城市(点)出发的旅行商(蚂蚁)来说是固定的值,所以可以提前计算好
t+=1
for k in range(m):
pk = p[k]
i = int(current_cities[k])
# 分母对于在一轮迭代中对于在同一个点出发的蚂蚁来说是固定的值
summation_s_in_allowed_tau = np.sum(tau[i][allowed[k]==1])
for j in range(n):
if allowed[k][j] == 0:
pk[i][j]=0
else:
pk[i][j]= tau[i][j] /summation_s_in_allowed_tau
分析上述公式, 如果分叉选项太多的话容易导致收敛慢,我们考虑加入先验知识:比如主要走看起来近一些的路
P i j k ( t ) = { [ τ i j ( t ) ] α × [ 1 d i j ( t ) ] β ∑ s ∈ a l l o w e d k [ τ i s ( t ) ] α × [ 1 d i s ( t ) ] β , j ∈ a l l o w e d k 0 , j ∉ a l l o w e d k P_{ij}^k(t)= \left \{ \begin{array}{ll} \frac{[\tau_{ij}(t)]^\alpha \times [\frac{1}{d_{ij}(t)}]^\beta} {\sum_{s\in allowed_k}[\tau_{is}(t)]^\alpha \times [\frac{1}{d_{is}(t)}]^\beta}, & j\in allowed_k\\ 0, & j\notin allowed_k \end{array} \right. Pijk(t)=⎩ ⎨ ⎧∑s∈allowedk[τis(t)]α×[dis(t)1]β[τij(t)]α×[dij(t)1]β,0,j∈allowedkj∈/allowedk
信息素浓度一样时,城市(点)i到城市(点)j的路径距离越小、1/d_{ij}(t)越大、概率值也就越大
其中α和 β 是为了调整信息素浓度和先验知识对概率的影响,当α越大,信息素浓度影响越大,当β越大,先验知识影响越大
- 当β为0 选择路径的概率完全由信息素浓度决定,为正反馈的启发式算法,缺点是收敛可能过慢
- 当α为0 选择路径的概率完全由先验知识决定,为贪心算法,缺点是可能陷入局部最优解
这里我也把代码放在这里,大家可以参考着使用,但是在本篇文章中我们不使用这个概率计算方式。
#参数初始化
alpha = 2
beta = 2
# 分母对于在一轮迭代中对于在同一个点出发的蚂蚁来说是固定的值
summation_s_in_allowed_tau_alpha_power_times_1_divided_by_dis_power_beta \
= np.sum(
np.power(tau[i][allowed[k]==1],alpha)
*np.power(1/d[i][allowed[k]==1],beta)
)
#计算概率
if allowed[k][j] == 0:
pk[i][j]=0
else:
pk[i][j]= np.power(tau[i][j],alpha)*np.power(1/d[i][j],beta) /summation_s_in_allowed_tau_alpha_power_times_1_divided_by_dis_power_beta
轮盘赌决定下一个点 到达下一个点 更新信息
我们并非直接选择概率最大的路线作为我们旅行商(蚂蚁)的路线,而是选用轮盘赌的形式决定旅行商的去向,这样子使旅行商(蚂蚁)们的路线更多样化,不容易陷入局部最优。
效率起见,我们其实可以在计算p[k][i][j]时一边进行轮盘赌,如果赌到了后面的概率也不需要计算了,这样子的话可以节省很多时间,但是为了更为直观的体现我们的算法,这里我就不采取这种方法。
roulette =random.random()
current_probability = 0
for j in range(n):
current_probability+=pk[i][j]
# 如果赌到了
if current_probability >roulette:
# 记录一下路线
move[i][j][k]=1
# 更改一下当前点
current_cities[k]=j
# 记录一下已经来过j,allowed中去除j
allowed[k][j]=0
# 第k只蚂蚁总路线加长
L[k]+=d[i][j]
# 后面就不用赌了
break
返回起点 更新信息
在整个allowed为空之后 ,注意题目的要求,题目要求是需要返回起点的,所以我们走完全程后还需要人为加上最后一步——返回起点
# 记得到达终点后还需要返回起点
for k in range(m):
# 获取一开始我们保存的start_cities[k]
start_city = start_cities[k]
# 获取一开始蚂蚁们最后到达的城市
final_city = current_cities[k]
# 记录一下路线
move[final_city][start_city][k]=1
# 更改一下当前点
current_cities[k]=start_city
# 第k只蚂蚁总路线加长
L[k]+=d[final_city][start_city]
更新迹浓度
迹浓度更新规则(ant-cycle算法)如下
τ i j ( t + 1 ) = ( 1 − ρ ) τ i j ( t ) + ∑ k = 1 m Δ τ i j k 其中 0 < ρ < 1 , Δ τ i j k = { Q L k , 第 k 只蚂蚁曾经过路径 i 到 j 0 , 其他 \tau_{ij}(t+1)=(1-\rho)\tau_{ij}(t)+\sum_{k=1}^m \Delta \tau_{ij}^k \\ 其中 0<\rho<1 ,\\ \Delta\tau_{ij}^k = \left \{ \begin{array}{ll} \frac{Q}{L_k}, &第k只蚂蚁曾经过路径i到j \\ 0, &其他 \end{array} \right. τij(t+1)=(1−ρ)τij(t)+k=1∑mΔτijk其中0<ρ<1,Δτijk={LkQ,0,第k只蚂蚁曾经过路径i到j其他
- ρ是挥发系数,ρ越大信息素挥发的越快
- L_k 是第k只蚂蚁走过的总路径长度
- Δτ_{ij}^k 是第k只蚂蚁路过i到j留下的信息素,这里我们选用的迹更新机制是ant-cycle,也就是以Q/L_k作为更新的值的机制,是蚁群算法提出者Marco Dorigo介绍的三种迹更新机制之一,还有两种分别是
- ant-density算法 以Q作为更新的值的机制
- ant-quantity算法 以Q/d_{ij}作为更新的值的机制
根据测试比较,其实是ant-cycle算法最好,因为它使用的是全局信息,而其它两个都是局部信息
for i in range(n):
for j in range(n):
# 注意 τ[i][j]的值是由move[i][j]和move[j][i]共同更新的,因为无论你从i到j还是从j到i 在i到j这段路程中迹浓度应当是一样的 前面有解释
tau[i][j]=(1-rho)*tau[i][j]+np.sum(Q/L[move[i][j]==1])+np.sum(Q/L[move[j][i]==1])
我们一般会在更新迹浓度的时候顺带保存一下当前迭代轮次的最短路径以及对应的长度
# 从L中找到最短的那个的下标best_k
best_k = np.argmin(L)
# 声明一个用来装最短路径的1维数组,长度为n+1
shortest_path = np.zeros(shape=(n+1),dtype=np.int)
# 最后一位放上当前点,因为当前点必然是最后一站
shortest_path[n]=current_cities[best_k]
# 通过move数组依次逆推出完整路径
for index in range(n-1,-1,-1):
j=shortest_path[index+1]
shortest_path[index]=np.argmax(move.T[best_k][j])
# 记录下路径以及长度
shortest_path_L_record[epoch]=L[best_k]
shortest_path_record[epoch]=shortest_path
# 打印路径以及长度
print(f"epoch {epoch} shortest_path: {shortest_path} distance:{L[best_k]}")
找到最短路径
我们有了shortest_path_record和shortest_path_L_record两个数组后我们可以很轻易地得到最短的路径,我们只需要找shortest_path_L_record中的最小值的下标然后再shortest_path_record中查找路径即可
best_epoch = np.argmin(shortest_path_L_record)
shortest_path_definite = shortest_path_record[best_epoch]
print(f"best_epoch {best_epoch} shortest_path: {shortest_path_definite} distance:{shortest_path_L_record[best_epoch]}")
完整代码
import random
import numpy as np
# 蚂蚁数
m = 2
# 城市数
n = 4
# 生成一张图
d = np.array([[0,2,6,3],
[2,0,4,1],
[6,4,0,8],
[3,1,8,0]])
Q = 10
# 挥发率
rho = 0.5
#初始信息素浓度
tau_0 = 0.4
#初始化信息素浓度
tau = np.ones((n,n))*tau_0
# 自己到自己的信息素为0
for index in range(n):
tau[index][index]=0
# 迭代次数
n_epoch = 2
# 记录每一轮迭代的最短长度
shortest_path_L_record = np.zeros(n_epoch)
# 记录每一轮迭代的最短长度的路径
shortest_path_record = np.zeros(shape=(n_epoch,n+1))
for epoch in range(n_epoch):
# 记录第k只蚂蚁从i往j走的概率
p = np.zeros(shape=(m,n,n))
# 记录第k只蚂蚁可以往哪个城市移动
allowed = np.ones(shape=(m,n))
# 记录第k只蚂蚁当前所在的城市的array 初始化时让他们处于随机城市
current_cities = np.array(np.floor(np.random.random(m)*n),dtype=np.int)
# 记录第k只蚂蚁出发的城市
start_cities = current_cities.copy()
# 我们需要记录每一次的移动的路径 (后面迹更新机制要用到)
move = np.zeros(shape=(n,n,m),dtype=np.int)
# 在allowed中把当前所在的城市设置为不可去 即值为0
for index in range(m):
first_city = int(current_cities[index])
allowed[index][first_city]=0
# L代表的是这个蚂蚁走过的总长度 如果对于下面这个L的用处有疑惑 我建议可以继续往下看
L = np.zeros(shape=(m))
# 用于记录当前时刻
t=0
while allowed.max()!=0:
t+=1
for k in range(m):
pk = p[k]
i = int(current_cities[k])
# 分母对于在一轮迭代中对于在同一个点出发的蚂蚁来说是固定的值
summation_s_in_allowed_tau = np.sum(tau[i][allowed[k]==1])
for j in range(n):
if allowed[k][j] == 0:
pk[i][j]=0
else:
pk[i][j]= tau[i][j] /summation_s_in_allowed_tau
roulette =random.random()
current_probability = 0
for j in range(n):
current_probability+=pk[i][j]
# 如果赌到了
if current_probability >roulette:
# 记录一下路线
move[i][j][k]=1
# 更改一下当前点
current_cities[k]=j
# 记录一下已经来过j,allowed中去除j
allowed[k][j]=0
# 第k只蚂蚁总路线加长
L[k]+=d[i][j]
# 后面就不用赌了
break
# 记得到达终点后还需要返回起点
for k in range(m):
# 获取一开始我们保存的start_cities[k]
start_city = start_cities[k]
# 获取一开始蚂蚁们最后到达的城市
final_city = current_cities[k]
# 记录一下路线
move[final_city][start_city][k]=1
# 更改一下当前点
current_cities[k]=start_city
# 第k只蚂蚁总路线加长
L[k]+=d[final_city][start_city]
for i in range(n):
for j in range(n):
# 注意 τ[i][j]的值是由move[i][j]和move[j][i]共同更新的,因为无论你从i到j还是从j到i 在i到j这段路程中迹浓度应当是一样的 前面有解释
tau[i][j]=(1-rho)*tau[i][j]+np.sum(Q/L[move[i][j]==1])+np.sum(Q/L[move[j][i]==1])
# 从L中找到最短的那个的下标best_k
best_k = np.argmin(L)
# 声明一个用来装最短路径的1维数组,长度为n+1
shortest_path = np.zeros(shape=(n+1),dtype=np.int)
# 最后一位放上当前点,因为当前点必然是最后一站
shortest_path[n]=current_cities[best_k]
# 通过move数组依次逆推出完整路径
for index in range(n-1,-1,-1):
j=shortest_path[index+1]
shortest_path[index]=np.argmax(move.T[best_k][j])
# 记录下路径以及长度
shortest_path_L_record[epoch]=L[best_k]
shortest_path_record[epoch]=shortest_path
# 打印路径以及长度
print(f"epoch {epoch} shortest_path: {shortest_path} distance:{L[best_k]}")
best_epoch = np.argmin(shortest_path_L_record)
shortest_path_definite = shortest_path_record[best_epoch]
print(f"best_epoch {best_epoch} shortest_path: {shortest_path_definite} distance:{shortest_path_L_record[best_epoch]}")