POJ 2125 Destroy The Graph
这题搞两天！！坦白的说，我现在会实现，但是真正的原因、原理；我还是不太明白！悲哀啊！！崩溃死了！！
哈哈，好吧，我弱爆了！！！
刚看到这题的时候，就知道不在我的能力范围内，因为我都没学过----二分图的最小点权覆盖集----我只能感觉到它与二分图最小点的覆盖集相似~然后就是看一堆又一堆的解题报告……都是说转化成最小割的模型，最小割？听说过……但不知道是啥……然后就是搜最小割的文章，最终看Amber的对最小割应用的总结；讲的还不错，我也看懂了……也看懂了解法，但是我还是还是不太明白，为什么？（God，Please tell me why！）1.为什么求得的最大流就是最小点权；2.为什么所求的割边对应的点v、u就是所求的点，也就是覆盖了所有的边；没办法我就看一个图
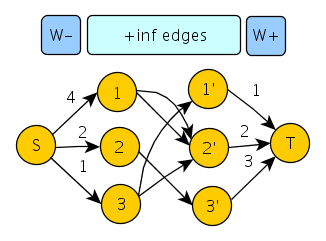就右边的一个图（额，这个图是一个博客上）我就盯着看盯着看、、今天下午我旁边那MM（队友）笑着给我说：请容许我说句话，你这图看了两天了；我苦笑着说道：是啊，看了两天了~~~~(>_<)~~~~
我就是看它：怎么会最大流等于最小点权、所求的点覆盖了所有边；也就是一直看这想着它的机理，似乎明白了一点，但是不成理论！没法用语言描述……到最后还是不太明白，谁可以清晰的告诉我Why？
解法：
二分图的最小点权覆盖集转化成最小割的模型
1.把每个点拆成两个点，即i：i、i+n；如图左边为出，右边为入
即可得到一个二分图。
2.在左部加一个源点S，右部加一个汇点T；建立S到左部的边和容量为W-，建立右部到T的边和容量为W+；中间v->u存在边则建立边、容量为无穷大；其他边（反向边）容量为0；即可得到一个二分的网络流图。
3.在网络流图中，求最大流==最小点权；求割边（割边只存在S->v或u->T中）的点v、u；v就是删除出度的点、u就是删除入度的点（不懂的话，搜一下最小割吧）。
在迷茫、疑惑、痛苦、挣扎中写出了下边的代码：
View Code
#include <stdio.h>
#include <memory.h>
#define N 202
#define M 10400
#define MAXVAL (1<<30)
int nodevp[N];
int nodeu[M],flow[M],next[M],ind;
//int cost[2][N];
int n,m,s,t;
void addedge(int v,int u,int val)
{
nodeu[ind]=u;
flow[ind]=val;
next[ind]=nodevp[v];
nodevp[v]=ind++;
}
void getDataAndBuildGraph()
{
int i,v,u,cost;
scanf("%d %d",&n,&m); s=0; t=2*n+1;
memset(nodevp,-1,sizeof(nodevp)); ind=0;
for(i=1;i<=n;i++)
{
scanf("%d",&cost);
addedge(i+n,t,cost);
addedge(t,i+n,0);
}
for(i=1;i<=n;i++)
{
scanf("%d",&cost);
addedge(s,i,cost);
addedge(i,s,0);
}
for(i=1;i<=m;i++)
{
scanf("%d %d",&v,&u);
addedge(v,u+n,MAXVAL);
addedge(u+n,v,0);
}
}
struct {int v,ind;} pre[N];
int queue[N],font,rear;
int Edmonds_Karp()
{
int i,v,u,minflow,maxflow=0;
while(1)
{
memset(pre,-1,sizeof(pre)); pre[s].v=0;
font=rear=0; queue[++rear]=s;
while(font<rear)
{
v=queue[++font];
for(i=nodevp[v];~i;i=next[i])
{
u=nodeu[i];
if(pre[u].v==-1 && flow[i])
{
pre[u].v=v; pre[u].ind=i;
queue[++rear]=u;
}
}
//调试① if(pre[n+1].v!=-1) break;这里坑爹坑大了!!! 2*n+1才是汇点!
if(pre[t].v!=-1) break;
}
// if(pre[n+1].v==-1) break;同上!!
if(pre[t].v==-1) break;
minflow=MAXVAL;
//调试② for(u=n+1; u ;u=pre[u].v)//悲剧了，u=n+1!尼玛啊!
for(u=t; u ; u=pre[u].v)
{
if(minflow>flow[pre[u].ind])
minflow=flow[pre[u].ind];
}
for(u=t; u ;u=pre[u].v)
{
flow[pre[u].ind]-=minflow;
flow[pre[u].ind ^1]+=minflow;
}
maxflow+=minflow;
}
return maxflow;
}
struct _{int v;char c;} record[N]; //本来想着改了DFS，这里的record就没必要了!可是还需要啊!
int flag[N],cnt;
/*
void DFS(int v)
{
int i,u;
flag[v]=1;
for(i=nodevp[v];~i;i=next[i])
{
u=nodeu[i];
if(flag[u]==0)
{
if(flow[i]==0)
{
//调试③，思路出错!源点0所连的点的边流量为0，不代表这个边就是割边!!!同理汇点一样
//所以这里写的都是错的! 需先DFS一下，标记从S出发能到达的点后，再去找!!
if(v==0) {record[++cnt].c='-'; record[cnt].v=u;}
else {record[++cnt].c='+';record[cnt].v=v-n;}
// if(u==(2*n+1)) {record[++cnt].c='+'; record[cnt].v=v-n; }
}
else DFS(u);
}
}
}*/
void DFS(int v)
{
int i,u;
flag[v]=1;
for(i=nodevp[v];~i;i=next[i])
{
u=nodeu[i];
if(!flag[u] && flow[i]!=0)
{
DFS(u);
}
}
}
void solve()
{
int i;
getDataAndBuildGraph();
printf("%d\n",Edmonds_Karp());
memset(flag,0,sizeof(flag));
DFS(0); cnt=0;
// printf("%d\n",cnt);
// for(i=1;i<=cnt;i++)
// {
// printf("%d %c\n",record[i].v,record[i].c);
// }
for(i=1;i<=n;i++)
if(flag[i]==0) record[++cnt].c='-',record[cnt].v=i;
for(i=n+1;i<=2*n;i++)
if(flag[i]==1) record[++cnt].c='+',record[cnt].v=i-n;
printf("%d\n",cnt);
for(i=1;i<=cnt;i++)
printf("%d %c\n",record[i].v,record[i].c);
}
int main()
{
freopen("input.txt","r",stdin);
solve();
return 0;
}
用时188ms 大牛们都是0ms
我想主要是因为求最大流我用的最笨的Edmonds_Karp算法，看人家都是SAP，额，我不会这个，该学学这个了！
今天上午2012-3-22又学了学SAP，啊，看了半天的SAP代码，算是看懂了、、看懂实现了。。。。
其中的某些原因还是不清楚。。
好吧，贴上SAP版的代码吧
View Code
#include <stdio.h>
#include <memory.h>
#define N 202
#define M 10400
#define MAXVAL (1<<30)
int nodevp[N];
int nodeu[M],flow[M],next[M],ind;
//int cost[2][N];
int n,m,s,t;
void addedge(int v,int u,int val)
{
nodeu[ind]=u;
flow[ind]=val;
next[ind]=nodevp[v];
nodevp[v]=ind++;
}
void getDataAndBuildGraph()
{
int i,v,u,cost;
scanf("%d %d",&n,&m); s=0; t=2*n+1;
memset(nodevp,-1,sizeof(nodevp)); ind=0;
for(i=1;i<=n;i++)
{
scanf("%d",&cost);
addedge(i+n,t,cost);
addedge(t,i+n,0);
}
for(i=1;i<=n;i++)
{
scanf("%d",&cost);
addedge(s,i,cost);
addedge(i,s,0);
}
for(i=1;i<=m;i++)
{
scanf("%d %d",&v,&u);
addedge(v,u+n,MAXVAL);
addedge(u+n,v,0);
}
}
int cur[N],dist[N],cnt_[N],pre[N];
int SAP()
{
int i,v,u,minflow=MAXVAL,maxflow=0;
memset(dist,0,sizeof(dist));
memset(cnt_,0,sizeof(cnt_));
memcpy(cur,nodevp,sizeof(nodevp));
cnt_[0]=t+1; v=0;
while(1)
{
// for(minflow=MAXVAL,i=cur[v]; ~i ; )又想了...MAXVAL夹在这里不对!!
// 因为可能把更小的流量丢了!!!所以它的这个策略是：宁小勿大!!
for(i=cur[v]; ~i ; )
{
u=nodeu[i];
if(flow[i] && dist[v]==dist[u]+1)
{
cur[v]=i; pre[u]=v;
minflow=flow[i]<minflow?flow[i]:minflow;
if(u==t)
{
maxflow+=minflow;
while(u!=0)
{
u=pre[u];
flow[cur[u]]-=minflow;
flow[cur[u]^1]+=minflow;
}
minflow=MAXVAL;
}
v=u; i=cur[v];
}
else i=next[i];
}
if(--cnt_[dist[v]]==0) break;
for(dist[v]=t+1,i=nodevp[v];~i;i=next[i])
{
u=nodeu[i];
if(flow[i] && dist[v]>dist[u])
dist[v]=dist[u],cur[v]=i;
}
dist[v]++; cnt_[dist[v]]++;
if(v==0) { if(dist[0]>t) break; minflow=MAXVAL; }
//这里我加的这个MAXVAL，是尽量减少minflow所受的干扰!!但是还是没法避免!
else v=pre[v];
}
return maxflow;
}
struct _{int v;char c;} record[N]; //本来想着改了DFS，这里的record就没必要了!可是还需要啊!
int flag[N],cnt;
void DFS(int v)
{
int i,u;
flag[v]=1;
for(i=nodevp[v];~i;i=next[i])
{
u=nodeu[i];
if(!flag[u] && flow[i]!=0)
{
DFS(u);
}
}
}
void solve()
{
int i;
getDataAndBuildGraph();
printf("%d\n",SAP());
memset(flag,0,sizeof(flag));
DFS(0); cnt=0;
// printf("%d\n",cnt);
// for(i=1;i<=cnt;i++)
// {
// printf("%d %c\n",record[i].v,record[i].c);
// }
for(i=1;i<=n;i++)
if(flag[i]==0) record[++cnt].c='-',record[cnt].v=i;
for(i=n+1;i<=2*n;i++)
if(flag[i]==1) record[++cnt].c='+',record[cnt].v=i-n;
printf("%d\n",cnt);
for(i=1;i<=cnt;i++)
printf("%d %c\n",record[i].v,record[i].c);
}
int main()
{
freopen("input.txt","r",stdin);
solve();
return 0;
}
郁闷，用时在16-100+中徘徊！最好时间16ms。额，可能是Special Judge的原因吧
额，再来个非递归的Dinic版的吧
View Code
#include <stdio.h>
#include <memory.h>
#define N 202
#define M 10400
#define MAXVAL (1<<30)
int nodevp[N];
int nodeu[M],flow[M],next[M],ind;
//int cost[2][N];
int n,m,s,t;
void addedge(int v,int u,int val)
{
nodeu[ind]=u;
flow[ind]=val;
next[ind]=nodevp[v];
nodevp[v]=ind++;
}
void getDataAndBuildGraph()
{
int i,v,u,cost;
scanf("%d %d",&n,&m); s=0; t=2*n+1;
memset(nodevp,-1,sizeof(nodevp)); ind=0;
for(i=1;i<=n;i++)
{
scanf("%d",&cost);
addedge(i+n,t,cost);
addedge(t,i+n,0);
}
for(i=1;i<=n;i++)
{
scanf("%d",&cost);
addedge(s,i,cost);
addedge(i,s,0);
}
for(i=1;i<=m;i++)
{
scanf("%d %d",&v,&u);
addedge(v,u+n,MAXVAL);
addedge(u+n,v,0);
}
}
int nextnodevp[N],level[N],queue[N],font,rear,top;
int Dinic()
{
int i,v,u,val,flag,minflow,maxflow=0;
while(1)
{
memset(level,0,sizeof(level));
font=rear=0; queue[++rear]=0; level[0]=1;
while(font<rear)
{
v=queue[++font];
for(i=nodevp[v];~i;i=next[i])
{
u=nodeu[i]; val=flow[i];
if(val && level[u]==0)
{
level[u]=level[v]+1;
queue[++rear]=u;
}
}
if(level[t]!=0) break;
}
if(level[t]==0) break;
memcpy(nextnodevp,nodevp,sizeof(nodevp));
nodeu[M-1]=0; top=0; queue[++top]=M-1;
while(top)
{
v=nodeu[queue[top]];
for(i=nextnodevp[v];~i;/*i=next[i]*/)
{
u=nodeu[i]; val=flow[i];
if(val && level[u]==level[v]+1)
{
queue[++top]=i;
nextnodevp[v]=next[i];
// break;
if(u==t)
{
minflow=MAXVAL;
for(i=2;i<=top;i++)
{
if(minflow>flow[queue[i]])
minflow=flow[queue[i]];
}
for(i=top;i>1;i--)
{
if(minflow==flow[queue[i]]) flag=i;
flow[queue[i]]-=minflow;
flow[queue[i]^1]+=minflow;
}
top=flag-1;
maxflow+=minflow;
u=nodeu[queue[top]];
}
v=u; i=nextnodevp[v];
}
else i=next[i];
}
top--; nextnodevp[v]=-1;
}
}
return maxflow;
}
struct _{int v;char c;} record[N]; //本来想着改了DFS，这里的record就没必要了!可是还需要啊!
int flag[N],cnt;
void DFS(int v)
{
int i,u;
flag[v]=1;
for(i=nodevp[v];~i;i=next[i])
{
u=nodeu[i];
if(!flag[u] && flow[i]!=0)
{
DFS(u);
}
}
}
void solve()
{
int i;
getDataAndBuildGraph();
printf("%d\n",Dinic());
memset(flag,0,sizeof(flag));
DFS(0); cnt=0;
for(i=1;i<=n;i++)
if(flag[i]==0) record[++cnt].c='-',record[cnt].v=i;
for(i=n+1;i<=2*n;i++)
if(flag[i]==1) record[++cnt].c='+',record[cnt].v=i-n;
printf("%d\n",cnt);
for(i=1;i<=cnt;i++)
printf("%d %c\n",record[i].v,record[i].c);
}
int main()
{
solve();
return 0;
}