朴素贝叶斯（Naive Bayes model）

朴素贝叶斯是一种基于贝叶斯定理和特征条件独立假设的分类算法。

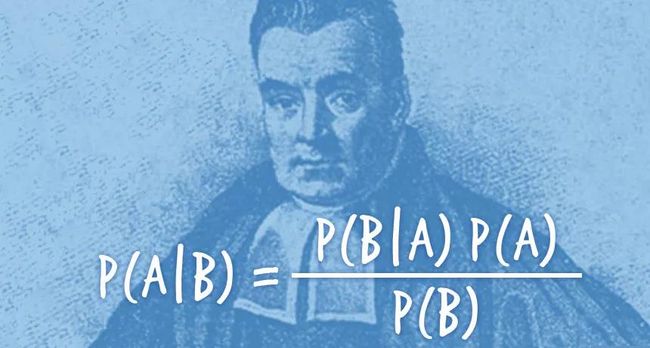
简单而言，对于给定的训练数据，朴素贝叶斯先基于特征条件独立假设学习输入和输出的联合概率分布，然后基于此分布对于新的实例，利用贝叶斯定理计算出最大的后验概率。朴素贝叶斯不会直接学习输入输出的联合概率分布，而是通过学习类的先验概率 和类条件概率 来完成。

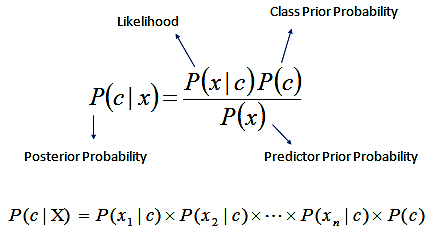
所谓朴素贝叶斯中朴素的含义，即特征条件独立假设，条件独立假设就是说用于分类的特征在类确定的条件下都是条件独立的。这一假设使得朴素贝叶斯的学习成为可能。朴素贝叶斯算法具体步骤如下。

首先计算类先验概率：

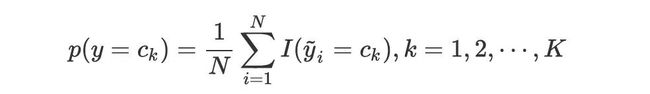
类先验概率可直接用极大似然估计进行计算。

然后计算类条件概率：

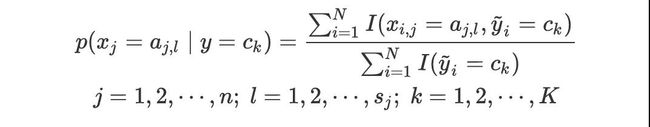
最后给定新的实例，计算其对应的最大后验概率，然后判断其所属的类别：

import numpy as  np
import pandas as pd

class Naive_Bayes:
    def __init__(self):
        pass

    # 朴素贝叶斯训练过程
    def nb_fit(self, X, y):
        classes = y[y.columns[0]].unique()
        class_count = y[y.columns[0]].value_counts()
        # 类先验概率
        class_prior = class_count / len(y)
        # 计算类条件概率
        prior = dict()
        for col in X.columns:
            for j in classes:
                p_x_y = X[(y == j).values][col].value_counts()
                for i in p_x_y.index:
                    prior[(col, i, j)] = p_x_y[i] / class_count[j]

        return classes, class_prior, prior

    # 预测新的实例
    def predict(self, X_test):
        res = []
        for c in classes:
            p_y = class_prior[c]
            p_x_y = 1
            for i in X_test.items():
                p_x_y *= prior[tuple(list(i) + [c])]
            res.append(p_y * p_x_y)
        return classes[np.argmax(res)]


if __name__ == "__main__":
    x1 = [1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3]
    x2 = ['S', 'M', 'M', 'S', 'S', 'S', 'M', 'M', 'L', 'L', 'L', 'M', 'M', 'L', 'L']
    y = [-1, -1, 1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1]
    df = pd.DataFrame({'x1': x1, 'x2': x2, 'y': y})
    X = df[['x1', 'x2']]
    y = df[['y']]
    X_test = {'x1': 2, 'x2': 'S'}

    nb = Naive_Bayes()
    classes, class_prior, prior = nb.nb_fit(X, y)
    print('测试数据预测类别为：', nb.predict(X_test))