机器学习实战(1)——房价预测
文章目录
- 一. 对于文章涉及知识的学习
-
- (1)数据处理——数据标准化
- (2)欧式距离与马曼哈顿距离
- (3)多项式拟合
- 二. 对于文章的理解
本文章的是基于另外一位博主文章的分析型文章,读者可先行阅读此文章再来看我的文章
Python机器学习房价预测 (斯坦福大学机器学习课程)
机器学习的步骤简单的分为以下三步
步骤①数据获取与处理
步骤②选择与训练模型
步骤③评估与显示
一. 对于文章涉及知识的学习
(1)数据处理——数据标准化
1.为什么要进行数据标准化?
在现实生活中,一个目标变量(y)可以认为是由多个特征变量(x)影响和控制的,那么这些特征变量的量纲和数值的量级就会不一样.
比如x1 = 10000,x2 = 1,x3 = 0.5 可以很明显的看出特征x1和x2、x3存在量纲的差距;x1对目标变量的影响程度将会比x2、x3对目标变量的影响程度要大(可以这样认为目标变量由x1掌控,x2,x3影响较小,一旦x1的值出现问题,将直接的影响到目标变量的预测,把目标变量的预测值由x1独揽大权,会存在高风险的预测)而通过标准化处理,可以使得不同的特征变量具有相同的尺度(也就是说将特征的值控制在某个范围内),这样目标变量就可以由多个相同尺寸的特征变量进行控制,这样,在使用梯度下降法学习参数的时候,不同特征对参数的影响程度就一样了。比如在训练神经网络的过程中,通过将数据标准化,能够加速权重参数的收敛。
简而言之:对数据标准化的目的是消除特征之间的差异性,便于特征一心一意学习权重。
2.什么时候需要进行数据标准化,什么时候不需要进行数据标准化?
当原始数据不同维度上的特征的尺度(单位)不一致时,需要标准化步骤对数据进行预处理,反之则不需要进行数据标准化。
下面这几类问题一般都需要进行数据标准化:
| 1 | 回归问题 |
|---|---|
| 2 | 机器学习算法 |
| 3 | 训练神经网络 |
| 4 | 聚类问题 |
| 5 | 分类问题 |
| 6 | 主成分分析(PCA)问题 |
3.如何进行标准化
实际上标准化包含如下多种方法:
| 方法名 | 作用 | 数学 公式 | 资料 |
|---|---|---|---|
| z-score标准化 | 实现中心化和正态分布 | x ∗ = x − x ‾ σ x^*=\frac{x-\overline{x}}{\sigma} x∗=σx−x ( x ∗ = x − m e a n s t d ) (x^*=\frac{x-mean}{std}) (x∗=stdx−mean) | 机器学习——特征工程——数据的标准化(Z-Score,Maxmin,MaxAbs,RobustScaler,Normalizer) |
| Min-Max | 归一化 | x ∗ = x − m i n m a x − m i n x^*=\frac{x-min}{max-min} x∗=max−minx−min | 机器学习——特征工程——数据的标准化(Z-Score,Maxmin,MaxAbs,RobustScaler,Normalizer) |
| MaxAbs | 最大绝对值标准化 | x ∗ = x m a x x^*=\frac{x}{max} x∗=maxx | 机器学习——特征工程——数据的标准化(Z-Score,Maxmin,MaxAbs,RobustScaler,Normalizer) |
| RobustScaler | 去除中值,根据分位数范围进行缩放 | x ∗ = x − Q ( 50 ) Q ( 75 ) − Q ( 25 ) x^*=\frac{x-Q(50)}{Q(75)-Q(25)} x∗=Q(75)−Q(25)x−Q(50)(Q表示分位数) | RobustScaler的计算方法/原理 |
这是机器学习的底层数学原理,如果实现又有多种方法(sklean,numpy……)
具体实现方法将在以后实现。
(2)欧式距离与马曼哈顿距离
两点直接的直线距离为欧式距离,而横纵坐标绝对值之和的值代表曼哈顿距离。
欧氏距离: d ( x , y ) = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + … … + ( x n − y n ) 2 = ∑ i = 1 n ( x i − y i ) 2 d(x,y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+……+(x_n-y_n)^2}=\sqrt{\sum_{i=1}^n{(x_i-y_i)}^2} d(x,y)=(x1−y1)2+(x2−y2)2+……+(xn−yn)2=∑i=1n(xi−yi)2
曼哈顿距离: L 1 ( x i , x j ) = ∑ i = 1 n ∣ x i l − x j l ∣ L_1(x_i,x_j)=\sum_{i=1}^n{|x_{i}^{l}-x^{l}_{j}|} L1(xi,xj)=∑i=1n∣xil−xjl∣
(3)多项式拟合
参考文献:
多项式函数曲线拟合——最小二乘法
二. 对于文章的理解
1.首先,导入相应的库(但这里并没有用到sklearn库)
# 导入需要用到的库
import numpy as np
import matplotlib.pyplot as plt
2.导入数据(采集数据)
# 定义存储输入数据(x)和目标数据(y)的数组
x, y = [], []
# 遍历数据集,变量sample对应的正是一个个样本
for sample in open("D:\\Users\\gedin\\Desktop\\1.txt", 'r'):
_x, _y = sample.split(",")
# 将字符串数据转化为浮点数
x.append(float(_x))
y.append(float(_y))
# 读取完数据后,将他们转化为Numpy数组以方便进一步的处理
x, y = np.array(x), np.array(y)
这里用到了txt文件读取,和对txt文件的相关操作
使用numpy.array将数据转化为数组方便后续操作
3.数据预处理与原始数据可视化
# 标准化
x = (x - x.mean()) / x.std()
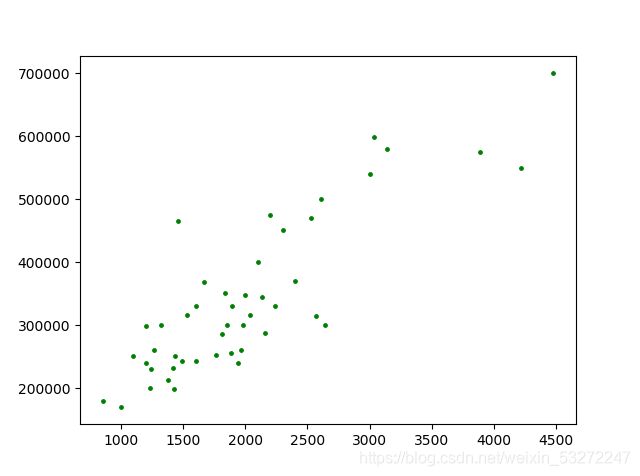
# 将原始数据集以散点的形式画出
plt.figure()
plt.scatter(x, y, c="g", s=6)
plt.show()
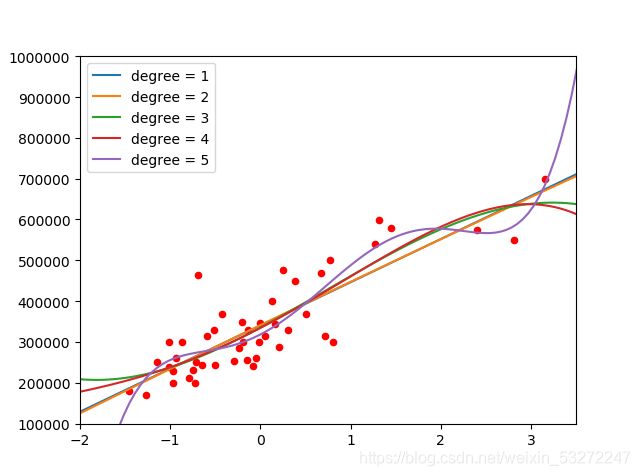
这里使用了 z − s c o r e 标 准 化 z-score标准化 z−score标准化,画出来的图像如下

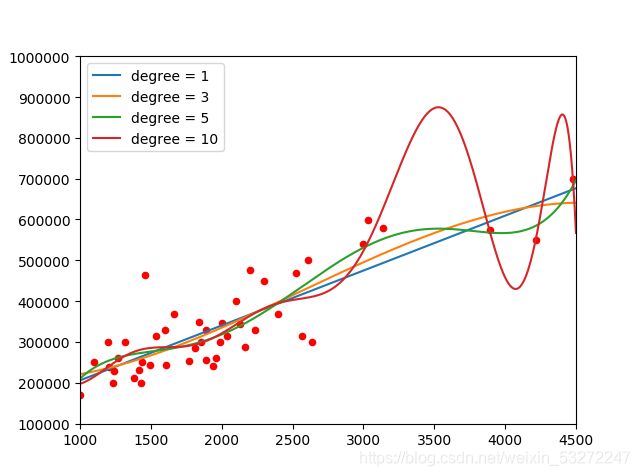
如果不进行标准化,图像将长下面这样:
你没有看错和前面一模一样,只是x轴范围缩小了
待会就知道它的作用了
4.建立模型
# (-2,4)这个区间上取100个点作为画图的基础
x0 = np.linspace(-2, 4, 100)
# 利用Numpy的函数定义训练并返回多项式回归模型的次数
# deg参数代表着模型参数中的n,即模型中多项式的次数
# 返回的模型能够根据输入的x(默认是x0),返回预测的y
def get_model(deg):
return lambda input_x=x0: np.polyval(np.polyfit(x, y ,deg), input_x)
【polyfit】多项式曲线拟合
【polyval】多项式曲线求值
5.计算损失
# 根据参数n、输入的x,y返回相对应的损失
def get_cost(deg, input_x,input_y):
return 0.5 * ((get_model(deg)(input_x) - input_y) ** 2).sum()
6.训练测试模型并画出各种模型
# 画出相应的图像
plt.scatter(x, y, c="r", s=20)
for d in test_set:
plt.plot(x0, get_model(d)(), label="degree = {}".format(d))
# 将横轴和纵轴的范围分别限制在(-2,4)和(10^5,10^6)
plt.xlim(-2, 4)
plt.ylim(1e5, 1e6)
# 调用legend方法使曲线对应的label正确显示
plt.legend()
plt.show()
可以看出没有进行标准化的图像和进行标准化的图像的差距
进行标准化的图像可以很明显看出不同模型的区别(有利于选择模型)
而没有进行标准化的图像各个模型无法分辨区别(不利于选择模型,是否过度拟合无法直接看出),只有当次数比较高时候才会明显看到区别
源码
""""
1
"""
# 导入需要用到的库
import numpy as np
import matplotlib.pyplot as plt
# 定义存储输入数据(x)和目标数据(y)的数组
x, y = [], []
# 遍历数据集,变量sample对应的正是一个个样本
for sample in open("D:\\Users\\gedin\\Desktop\\1.txt", 'r'):
_x, _y = sample.split(",")
# 将字符串数据转化为浮点数
x.append(float(_x))
y.append(float(_y))
# 读取完数据后,将他们转化为Numpy数组以方便进一步的处理
x, y = np.array(x), np.array(y)
# 标准化
#x = (x - x.mean()) / x.std()
# 将原始数据集以散点的形式画出
plt.figure()
plt.scatter(x, y, c="g", s=6)
plt.show()
"""
2
"""
# (-2,4)这个区间上取100个点作为画图的基础
x0 = np.linspace(1000, 4500, 10000)
# 利用Numpy的函数定义训练并返回多项式回归模型的次数
# deg参数代表着模型参数中的n,即模型中多项式的次数
# 返回的模型能够根据输入的x(默认是x0),返回预测的y
def get_model(deg):
return lambda input_x=x0: np.polyval(np.polyfit(x, y ,deg), input_x)
""""
3
"""
# 根据参数n、输入的x,y返回相对应的损失
def get_cost(deg, input_x,input_y):
return 0.5 * ((get_model(deg)(input_x) - input_y) ** 2).sum()
# 定义测试函数集并根据它进行各种实验
test_set = (1,2,3,4,5)
for d in test_set:
# 输出损失
print(get_cost(d, x, y))
# 画出相应的图像
plt.scatter(x, y, c="r", s=20)
for d in test_set:
plt.plot(x0, get_model(d)(), label="degree = {}".format(d))
# 将横轴和纵轴的范围分别限制在(-2,4)和(10^5,10^6)
plt.xlim(1000, 4500)
plt.ylim(1e5, 1e6)
# 调用legend方法使曲线对应的label正确显示
plt.legend()
plt.show()