LQR、MPC以及osqp库
目录
- LQR
-
- lqr问题模型
- MPC
-
- mpc问题模型
- 使用osqp计算mpc问题
- osqp库
-
- 安装
- 使用
最优控制是指在给定的约束条件下,寻求一个控制,使给定的系统性能指标达到极大值(或极小值)。
LQR
lqr问题模型
LQR最优控制方法小结
控制理论:离散及连续的LQR控制算法原理推导
MPC
mpc问题模型
关于mpc的介绍可以参考链接:
现代控制理论-控制基础与控制算法杂烩
使用osqp计算mpc问题
MPC问题都可以转换为QP问题来进行求解,QP问题的一般形式:
m i n J = − 1 2 x T H x + g T x min J = -\frac{1}{2}x^T H x + g^Tx minJ=−21xTHx+gTx
s . t . a ≤ A x ≤ b s.t. \ \ \ a \le Ax \leq b s.t. a≤Ax≤b
其中,H是对称矩阵(Hessian矩阵),g是梯度向量Jacobi矩阵,x是待优化变量。
现有一通用MPC问题:
MPC问题通用表述
目标为最小化代价函数:
m i n i m i z e J = ( x N − x r ) T Q N ( x N − x r ) + ∑ k = 0 N − 1 ( x k − x r ) T Q ( x k − x r ) + u k T R u k minimize J = (x_N - x_r)^TQ_N(x_N - x_r) + \sum_{k=0}^{N-1} (x_k - x_r)^TQ(x_k - x_r) + u_k^TRu_k minimizeJ=(xN−xr)TQN(xN−xr)+∑k=0N−1(xk−xr)TQ(xk−xr)+ukTRuk
其中 N N N为最大的预测时域, x r x_r xr为参考状态,即预测的输入要让系统又快又稳地接近参考状态。
等式约束(线性系统状态离散转移方程):
x k + 1 = A x k + B u k x_{k+1} = Ax_k + Bu_k xk+1=Axk+Buk
k+1时刻系统状态与k时刻状态和k时刻输入线性相关。
不等式约束(系统状态、输入约束/状态输入边界):
x m i n ≤ x k ≤ x m a x x_{min} \leq x_k \leq x_{max} xmin≤xk≤xmax
u m i n ≤ u k ≤ u m a x u_{min} \leq u_k \leq u_{max} umin≤uk≤umax
系统0时刻(即当前时刻)状态已知
x 0 = x ˉ x_{0}= \bar{x} x0=xˉ
将该MPC问题转化为QP问题:
1.由状态转移方程 x k + 1 = A x k + B u k x_{k+1} = Ax_k + Bu_k xk+1=Axk+Buk得
x 1 = A x 0 + B u 0 x_{1} = Ax_0 + Bu_0 x1=Ax0+Bu0
x 2 = A x 1 + B u 1 = A ( A x 0 + B u 0 ) + B u 1 = A 2 x 0 + A B u 0 + B u 1 x_{2} = Ax_1 + Bu_1 = A(Ax_0 + Bu_0) + Bu_1=A^2x_0+ABu_0+Bu_1 x2=Ax1+Bu1=A(Ax0+Bu0)+Bu1=A2x0+ABu0+Bu1
…
x N = A x N − 1 + B u N − 1 = A N x 0 + A N − 1 B u 0 + A N − 2 B u 1 + . . . + B u N − 1 x_{N} = Ax_{N-1} + Bu_{N-1} =A^Nx_0+A^{N-1}Bu_0+A^{N-2}Bu_1+...+Bu_{N-1} xN=AxN−1+BuN−1=ANx0+AN−1Bu0+AN−2Bu1+...+BuN−1
由上式可看出,系统未来N时刻内状态 x 1 , x 2 . . . x N x_{1} , x_{2}...x_{N} x1,x2...xN可由当前状态 x 0 x_{0} x0和当前时刻输入 u 0 u_{0} u0预测得出。
整理等式成矩阵形式:

X = M x 0 + C U X = Mx_0 + CU X=Mx0+CU
import osqp
import numpy as np
import scipy as sp
from scipy import sparse
# Discrete time model of a quadcopter
# x_{k+1} = Ad x_{k} + Bd u_{k}
Ad = sparse.csc_matrix([
[1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0., 0., 0. ],
[0., 1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0., 0. ],
[0., 0., 1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0. ],
[0.0488, 0., 0., 1., 0., 0., 0.0016, 0., 0., 0.0992, 0., 0. ],
[0., -0.0488, 0., 0., 1., 0., 0., -0.0016, 0., 0., 0.0992, 0. ],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.0992],
[0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0. ],
[0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0. ],
[0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0. ],
[0.9734, 0., 0., 0., 0., 0., 0.0488, 0., 0., 0.9846, 0., 0. ],
[0., -0.9734, 0., 0., 0., 0., 0., -0.0488, 0., 0., 0.9846, 0. ],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.9846]
])
Bd = sparse.csc_matrix([
[0., -0.0726, 0., 0.0726],
[-0.0726, 0., 0.0726, 0. ],
[-0.0152, 0.0152, -0.0152, 0.0152],
[-0., -0.0006, -0., 0.0006],
[0.0006, 0., -0.0006, 0.0000],
[0.0106, 0.0106, 0.0106, 0.0106],
[0, -1.4512, 0., 1.4512],
[-1.4512, 0., 1.4512, 0. ],
[-0.3049, 0.3049, -0.3049, 0.3049],
[-0., -0.0236, 0., 0.0236],
[0.0236, 0., -0.0236, 0. ],
[0.2107, 0.2107, 0.2107, 0.2107]])
[nx, nu] = Bd.shape # nx nu 状态量数量 和输入量数量
# Constraints
u0 = 10.5916
umin = np.array([9.6, 9.6, 9.6, 9.6]) - u0
umax = np.array([13., 13., 13., 13.]) - u0
xmin = np.array([-np.pi/6,-np.pi/6,-np.inf,-np.inf,-np.inf,-1.,
-np.inf,-np.inf,-np.inf,-np.inf,-np.inf,-np.inf])
xmax = np.array([ np.pi/6, np.pi/6, np.inf, np.inf, np.inf, np.inf,
np.inf, np.inf, np.inf, np.inf, np.inf, np.inf])
# Objective function
Q = sparse.diags([0., 0., 10., 10., 10., 10., 0., 0., 0., 5., 5., 5.])
QN = Q
R = 0.1*sparse.eye(4)
# Initial and reference states
x0 = np.zeros(12)
xr = np.array([0.,0.,1.,0.,0.,0.,0.,0.,0.,0.,0.,0.])
# Prediction horizon
N = 10
上面为初始化问题模型,这一部分Ad,Bd 是转移方程矩阵
目标函数
m i n i m i z e J = ( x N − x r ) T Q N ( x N − x r ) + ∑ k = 0 N − 1 ( x k − x r ) T Q ( x k − x r ) + u k T R u k minimize J = (x_N - x_r)^TQ_N(x_N - x_r) + \sum_{k=0}^{N-1} (x_k - x_r)^TQ(x_k - x_r) + u_k^TRu_k minimizeJ=(xN−xr)TQN(xN−xr)+∑k=0N−1(xk−xr)TQ(xk−xr)+ukTRuk
变换成二次型一般形式:
m i n i m i z e J = ( x N − x r ) T Q N ( x N − x r ) + ∑ k = 0 N − 1 ( x k − x r ) T Q ( x k − x r ) + u k T R u k = x N T Q N x N − 2 x r T Q N x N + x r T Q N x r + ∑ k = 0 N − 1 ( x k T Q x k − 2 x r T Q x k + x r T Q x r ) + u k T R u k minimize J \\ = (x_N - x_r)^TQ_N(x_N - x_r) + \sum_{k=0}^{N-1} (x_k - x_r)^TQ(x_k - x_r) + u_k^TRu_k \\ = x_N^TQ_Nx_N - 2x_r^TQ_Nx_N + x_r^TQ_Nx_r + \sum_{k=0}^{N-1} (x_k ^TQx_k - 2x_r ^TQx_k + x_r ^TQx_r ) + u_k^TRu_k minimizeJ=(xN−xr)TQN(xN−xr)+∑k=0N−1(xk−xr)TQ(xk−xr)+ukTRuk=xNTQNxN−2xrTQNxN+xrTQNxr+∑k=0N−1(xkTQxk−2xrTQxk+xrTQxr)+ukTRuk
其中 x r T Q x r x_r ^TQx_r xrTQxr和 x r T Q N x r x_r ^TQ_Nx_r xrTQNxr都为已知状态量部分,与目标函数优化无关,在目标函数可写为:
m i n i m i z e J = x N T Q N x N + ∑ k = 0 N − 1 ( x k T Q x k ) + u k T R u k − 2 x r T Q N x N − ∑ k = 0 N − 1 ( 2 x r T Q x k ) minimize J \\ = x_N^TQ_Nx_N + \sum_{k=0}^{N-1} (x_k ^TQx_k ) + u_k^TRu_k- 2x_r^TQ_Nx_N - \sum_{k=0}^{N-1} (2x_r ^TQx_k ) minimizeJ=xNTQNxN+∑k=0N−1(xkTQxk)+ukTRuk−2xrTQNxN−∑k=0N−1(2xrTQxk)
合并状态量与输入量,令
y = [ x 0 , x 1 , x 2 . . . x N , x 0 , x 1 . . . x N − 1 ] T y = [x_0,x_1,x_2...x_N,x_0,x_1...x_{N-1}]^T y=[x0,x1,x2...xN,x0,x1...xN−1]T
则目标函数可写成矩阵形式:

令

则目标函数为 J = y T P y + 2 q T y J=y^TPy +2q^Ty J=yTPy+2qTy
# Cast MPC problem to a QP: x = (x(0),x(1),...,x(N),u(0),...,u(N-1))
# - quadratic objective
P = sparse.block_diag([sparse.kron(sparse.eye(N), Q), QN,
sparse.kron(sparse.eye(N), R)], format='csc')
# - linear objective
# np.ones(N) 1x10, -Q.dot(xr) 12x1, np.kron(np.ones(N), -Q.dot(xr)) 120x1
# -QN.dot(xr) 12x1 np.zeros(N*nu) 1x(10x4)
# 以上为个部分原始行列数,但由于1xn或nx1均为一维数组,在Numpy中都表现为:(n,),但在存储上均为1xn
# 如何看数组维度 : https://zhuanlan.zhihu.com/p/29022069?from_voters_page=true
# 最终q 1x120 + 1x12 + 1x40 = 1x172 显示为 shape=(172,0)
q = np.hstack([np.kron(np.ones(N), -Q.dot(xr)), -QN.dot(xr),
np.zeros(N*nu)]
构建等式约束关系:
由 x k + 1 = A x k + B u k x_{k+1} = Ax_k + Bu_k xk+1=Axk+Buk得
0 = A x k − x k + 1 + B u k = 0 0= Ax_k -x_{k+1} + Bu_k=0 0=Axk−xk+1+Buk=0
即有
− x 0 = 0 − x 0 + 0 = − x 0 -x_{0}= 0 -x_{0} +0=-x_{0} −x0=0−x0+0=−x0
0 = A x 0 − x 1 + B u 0 = 0 0= Ax_0 -x_{1} + Bu_0=0 0=Ax0−x1+Bu0=0
0 = A x 1 − x 2 + B u 1 = 0 0= Ax_1 -x_{2} + Bu_1=0 0=Ax1−x2+Bu1=0
。。
0 = A x N − 1 − x N + B u N − 1 = 0 0= Ax_{N-1} -x_{N} + Bu_{N-1}=0 0=AxN−1−xN+BuN−1=0
变换成矩阵形式:

leq、Ax、Bu、ueq如上所示。
则有 A e q = [ A x , B u ] Aeq=[Ax,Bu] Aeq=[Ax,Bu]
l e q = A e q y = u e q leq= A_{eq} \ y=ueq leq=Aeq y=ueq
leq有N+1行。
构建不等式约束关系:
由 x m i n ≤ x k ≤ x m a x x_{min} \leq x_k \leq x_{max} xmin≤xk≤xmax
u m i n ≤ u k ≤ u m a x u_{min} \leq u_k \leq u_{max} umin≤uk≤umax得
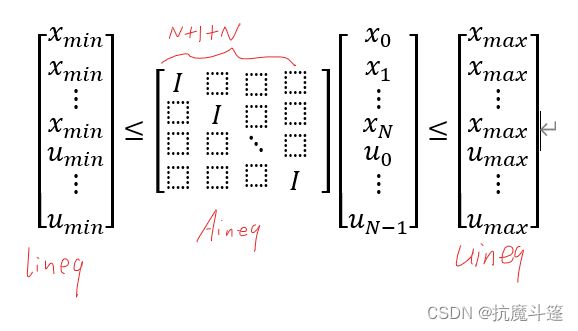
即 l i n e q ≤ A i n e q y ≤ u i n e q lineq\le A_{ineq} \ y \le uineq lineq≤Aineq y≤uineq
并合并等式与不等式约束关系:
l i n e q + l e q ≤ ( A i n e q + A e q ) y ≤ u i n e q + u e q lineq+leq \le (A_{ineq}+A_{eq})y \le uineq+ueq lineq+leq≤(Aineq+Aeq)y≤uineq+ueq
即最终约束为 l ≤ A y ≤ u l \le Ay \le u l≤Ay≤u
# - linear dynamics
# sparse.kron(sparse.eye(N+1),-sparse.eye(nx)) (11x12)x(11x12) = 132x132
# sparse.kron(sparse.eye(N+1, k=-1), Ad) (11x12)x(11x12) = 132x132
# 即Ax 132x132
Ax = sparse.kron(sparse.eye(N+1),-sparse.eye(nx)) + sparse.kron(sparse.eye(N+1, k=-1), Ad)
# sparse.csc_matrix((1, N)) 1x10, sparse.eye(N) 10x10 ,
# sparse.vstack([sparse.csc_matrix((1, N)) 11x10, Bd 12x4
# Bu (11x12)x(10x4)=132x40
Bu = sparse.kron(sparse.vstack([sparse.csc_matrix((1, N)), sparse.eye(N)]), Bd)
Aeq = sparse.hstack([Ax, Bu])
leq = np.hstack([-x0, np.zeros(N*nx)])
ueq = leq
# - input and state constraints
Aineq = sparse.eye((N+1)*nx + N*nu)
lineq = np.hstack([np.kron(np.ones(N+1), xmin), np.kron(np.ones(N), umin)])
uineq = np.hstack([np.kron(np.ones(N+1), xmax), np.kron(np.ones(N), umax)])
# - OSQP constraints
A = sparse.vstack([Aeq, Aineq], format='csc')
l = np.hstack([leq, lineq])
u = np.hstack([ueq, uineq])
至此,mpc问题已经转换为qp形式:
m i n i m i z e J = y T P y + 2 q T y minimize \ J=y^TPy +2q^Ty minimize J=yTPy+2qTy
s . t . l ≤ A y ≤ u s.t. \ \ l \le Ay \le u s.t. l≤Ay≤u
接下来使用osqp求解即可:
# Create an OSQP object
prob = osqp.OSQP()
# Setup workspace
prob.setup(P, q, A, l, u, warm_start=True)
# Simulate in closed loop
nsim = 1 #循环次数
for i in range(nsim):
# Solve
res = prob.solve()
# Check solver status
if res.info.status != 'solved':
raise ValueError('OSQP did not solve the problem!')
# my_result = res.info
# print(my_result)
print("res.x",res.x)
# Apply first control input to the plant
# ctrl
ctrl = res.x[-N*nu:-(N-1)*nu] # res.x[-N*nu:-(N-1)*nu]=res.x[(N+1)*nx:(N+1)*nx+nu]
# res.x为y=[x0, x1,..xN,u0,...uN-1]
print("ctrl",ctrl)
# ctrl2 = res.x[(N+1)*nx:(N+1)*nx+nu]
# print("ctrl2",ctrl2)
x0 = Ad.dot(x0) + Bd.dot(ctrl)
# Update initial state
# 更新l和u中leq和ueq部分的-x0
l[:nx] = -x0
u[:nx] = -x0
prob.update(l=l, u=u)
此例程完整代码为:
Model predictive control (MPC) python
带注释
import osqp
import numpy as np
import scipy as sp
from scipy import sparse
# Discrete time model of a quadcopter
# x_{k+1} = Ad x_{k} + Bd u_{k}
Ad = sparse.csc_matrix([
[1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0., 0., 0. ],
[0., 1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0., 0. ],
[0., 0., 1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0. ],
[0.0488, 0., 0., 1., 0., 0., 0.0016, 0., 0., 0.0992, 0., 0. ],
[0., -0.0488, 0., 0., 1., 0., 0., -0.0016, 0., 0., 0.0992, 0. ],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.0992],
[0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0. ],
[0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0. ],
[0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0. ],
[0.9734, 0., 0., 0., 0., 0., 0.0488, 0., 0., 0.9846, 0., 0. ],
[0., -0.9734, 0., 0., 0., 0., 0., -0.0488, 0., 0., 0.9846, 0. ],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.9846]
])
Bd = sparse.csc_matrix([
[0., -0.0726, 0., 0.0726],
[-0.0726, 0., 0.0726, 0. ],
[-0.0152, 0.0152, -0.0152, 0.0152],
[-0., -0.0006, -0., 0.0006],
[0.0006, 0., -0.0006, 0.0000],
[0.0106, 0.0106, 0.0106, 0.0106],
[0, -1.4512, 0., 1.4512],
[-1.4512, 0., 1.4512, 0. ],
[-0.3049, 0.3049, -0.3049, 0.3049],
[-0., -0.0236, 0., 0.0236],
[0.0236, 0., -0.0236, 0. ],
[0.2107, 0.2107, 0.2107, 0.2107]])
[nx, nu] = Bd.shape # nx nu 状态量数量 和输入量数量
# Constraints
u0 = 10.5916
umin = np.array([9.6, 9.6, 9.6, 9.6]) - u0
umax = np.array([13., 13., 13., 13.]) - u0
xmin = np.array([-np.pi/6,-np.pi/6,-np.inf,-np.inf,-np.inf,-1.,
-np.inf,-np.inf,-np.inf,-np.inf,-np.inf,-np.inf])
xmax = np.array([ np.pi/6, np.pi/6, np.inf, np.inf, np.inf, np.inf,
np.inf, np.inf, np.inf, np.inf, np.inf, np.inf])
# Objective function
Q = sparse.diags([0., 0., 10., 10., 10., 10., 0., 0., 0., 5., 5., 5.])
QN = Q
R = 0.1*sparse.eye(4)
# Initial and reference states
x0 = np.zeros(12)
xr = np.array([0.,0.,1.,0.,0.,0.,0.,0.,0.,0.,0.,0.])
# Prediction horizon
N = 10
# Cast MPC problem to a QP: x = (x(0),x(1),...,x(N),u(0),...,u(N-1))
# - quadratic objective
P = sparse.block_diag([sparse.kron(sparse.eye(N), Q), QN,
sparse.kron(sparse.eye(N), R)], format='csc')
# - linear objective
# np.ones(N) 1x10, -Q.dot(xr) 12x1, np.kron(np.ones(N), -Q.dot(xr)) 120x1
# -QN.dot(xr) 12x1 np.zeros(N*nu) 1x(10x4)
# 以上为个部分原始行列数,但由于1xn或nx1均为一维数组,在Numpy中都表现为:(n,),但在存储上均为1xn
# 如何看数组维度 : https://zhuanlan.zhihu.com/p/29022069?from_voters_page=true
# 最终q 1x120 + 1x12 + 1x40 = 1x172 显示为 shape=(172,0)
q = np.hstack([np.kron(np.ones(N), -Q.dot(xr)), -QN.dot(xr),
np.zeros(N*nu)])
# x1 = np.kron(np.ones(N), -Q.dot(xr))
# x2 = -Q.dot(xr)
# x3 = -QN.dot(xr)
# x4 = np.zeros(N*nu)
# print(q.shape)
# - linear dynamics
# sparse.kron(sparse.eye(N+1),-sparse.eye(nx)) (11x12)x(11x12) = 132x132
# sparse.kron(sparse.eye(N+1, k=-1), Ad) (11x12)x(11x12) = 132x132
# 即Ax 132x132
Ax = sparse.kron(sparse.eye(N+1),-sparse.eye(nx)) + sparse.kron(sparse.eye(N+1, k=-1), Ad)
# sparse.csc_matrix((1, N)) 1x10, sparse.eye(N) 10x10 ,
# sparse.vstack([sparse.csc_matrix((1, N)) 11x10, Bd 12x4
# Bu (11x12)x(10x4)=132x40
Bu = sparse.kron(sparse.vstack([sparse.csc_matrix((1, N)), sparse.eye(N)]), Bd)
Aeq = sparse.hstack([Ax, Bu])
leq = np.hstack([-x0, np.zeros(N*nx)])
ueq = leq
# - input and state constraints
Aineq = sparse.eye((N+1)*nx + N*nu)
lineq = np.hstack([np.kron(np.ones(N+1), xmin), np.kron(np.ones(N), umin)])
uineq = np.hstack([np.kron(np.ones(N+1), xmax), np.kron(np.ones(N), umax)])
# - OSQP constraints
A = sparse.vstack([Aeq, Aineq], format='csc')
print(A)
l = np.hstack([leq, lineq])
# print(l)
u = np.hstack([ueq, uineq])
# Create an OSQP object
prob = osqp.OSQP()
# Setup workspace
prob.setup(P, q, A, l, u, warm_start=True)
# print("P",P)
# print("q",q)
# print("A",A)
# print("l",l)
# print("u",u)
# Simulate in closed loop
nsim = 1
for i in range(nsim):
# Solve
res = prob.solve()
# Check solver status
if res.info.status != 'solved':
raise ValueError('OSQP did not solve the problem!')
# my_result = res.info
# print(my_result)
print("res.x",res.x)
# Apply first control input to the plant
# ctrl
ctrl = res.x[-N*nu:-(N-1)*nu] # res.x[-N*nu:-(N-1)*nu]=res.x[(N+1)*nx:(N+1)*nx+nu]
# res.x为y=[x0, x1,..xN,u0,...uN-1]
print("ctrl",ctrl)
ctrl2 = res.x[(N+1)*nx:(N+1)*nx+nu]
print("ctrl2",ctrl2)
# 更新系统状态,输入控制量后的状态
x0 = Ad.dot(x0) + Bd.dot(ctrl)
# Update initial state
# 更新l和u中leq和ueq部分的-x0
l[:nx] = -x0
u[:nx] = -x0
prob.update(l=l, u=u)
osqp库
安装
参考:Linux下osqp编译安装
sudo git clone --recursive https://github.com/oxfordcontrol/osqp
cd osqp
mkdir build
cd build
sudo cmake -G "Unix Makefiles" ..
sudo cmake --build .
sudo cmake --build . --target install
使用
在 CMake 项目中包含 OSQP:
# Find OSQP library and headers
find_package(osqp REQUIRED)
# Link the OSQP shared library
target_link_libraries(yourTarget PRIVATE osqp::osqp)
# or...
# Link the OSQP static library
target_link_libraries(yourTarget PRIVATE osqp::osqpstatic)
包含头文件:
#include // Load problem data
c_float P_x[3] = {4.0, 1.0, 2.0, };
c_int P_nnz = 3;
c_int P_i[3] = {0, 0, 1, };
c_int P_p[3] = {0, 1, 3, };
c_float q[2] = {1.0, 1.0, };
c_float A_x[4] = {1.0, 1.0, 1.0, 1.0, };
c_int A_nnz = 4;
c_int A_i[4] = {0, 1, 0, 2, };
c_int A_p[3] = {0, 2, 4, };
c_float l[3] = {1.0, 0.0, 0.0, };
c_float u[3] = {1.0, 0.7, 0.7, };
c_int n = 2;
c_int m = 3;
// Exitflag
c_int exitflag = 0;
// Workspace structures
OSQPWorkspace *work;
OSQPSettings *settings = (OSQPSettings *)c_malloc(sizeof(OSQPSettings));
OSQPData *data = (OSQPData *)c_malloc(sizeof(OSQPData));
// Populate data
if (data) {
data->n = n;
data->m = m;
data->P = csc_matrix(data->n, data->n, P_nnz, P_x, P_i, P_p);
data->q = q;
data->A = csc_matrix(data->m, data->n, A_nnz, A_x, A_i, A_p);
data->l = l;
data->u = u;
}
// Define solver settings as default
if (settings) {
osqp_set_default_settings(settings);
settings->alpha = 1.0; // Change alpha parameter
}
// Setup workspace
exitflag = osqp_setup(&work, data, settings);
// Solve Problem
osqp_solve(work);
//查看状态
auto status = work->info->status_val;
//查看结果
auto res = work->solution->x; //x是向量 x[0] x[1]...
// Cleanup
osqp_cleanup(work);
if (data) {
if (data->A) c_free(data->A);
if (data->P) c_free(data->P);
c_free(data);
}
if (settings) c_free(settings);
return exitflag;