斐波那契(黄金分割)查找算法 --- 简单易懂
目录
一、斐波那契推导公式
- 2.1、基本原理
- 2.2、基本思想
一、斐波那契推导公式
我们直接从现成的斐波那契数列入手,如下:斐波那契数列:
| F(1) | F(2) | F(3) | F(4) | F(5) | F(6) | F(7) | F(8) | F(9) | F(10) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
从上可知,从斐波那契数列第三项开始,每项的数值 = 前面两项数值之和,即 F(k) = F(k - 1) + F(k - 2)!
因此得出斐波那契数列的递推公式:
F ( 0 ) = 0 , F ( 1 ) = 1 F(0)=0, F(1)=1 F(0)=0,F(1)=1
F ( n ) = F ( n − 1 ) + F ( n − 2 ) ( n ≥ 2 , n ∈ N ∗ ) F(n)=F(n−1)+F(n−2)(n≥2,n∈N∗) F(n)=F(n−1)+F(n−2)(n≥2,n∈N∗)
二、斐波那契查找算法
2.1、基本原理
斐波那契基本原理图如下:
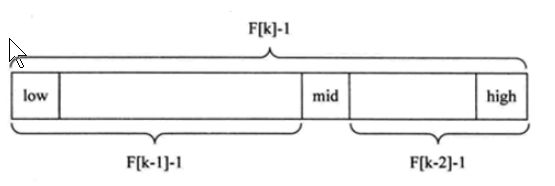
上图中,F 代表斐波那契数列,k 代表斐波那契数组索引!
例如:int[] f = {1, 1, 2, 3, 5, 13, 21, 34, 55},
其中 f[k = 0] = 1,f[k = 1] = 1,f[k = 2] = 2!
斐波那契查找算法的核心公式:
m i d = l o w + F ( k − 1 ) − 1 mid=low+F(k−1)−1 mid=low+F(k−1)−1
至于上面的这个公式,我个人认为,可以把 low = 0,看成是 mid = F(k - 1) - 1,也就是 mid = mid 前面的索引数相加,所以公式中的 low 初始索引值是 0,后面会变化!
斐波那契查找算法的核心公式和二分查找算法、插值查找算法的核心公式类似!在这里提一下后两种的核心公式!
二分查找算法的核心公式:
m i d = l o w + ( h i g h − l o w ) / 2 mid=low+(high - low) / 2 mid=low+(high−low)/2
插值查找算法的核心公式:
m i d = l o w + ( h i g h − l o w ) ∗ ( t a r g e t − a r r [ l o w ] ) / ( a r r [ h i g h ] − a r r [ l o w ] ) mid=low+(high - low) * (target - arr[low]) / (arr[high] - arr[low]) mid=low+(high−low)∗(target−arr[low])/(arr[high]−arr[low])
回到正题,通过 F[k] = F[k - 1] + F[k + 1](1),我们可以推出 F[k] - 1 = (F[k -1] - 1) + (F[k - 2] - 1) + 1(2),客观上说,(2)式中的 + 1 就相当于 + mid(哈哈哈)!
2.1、基本思想
举个例子,有一个 数组 int[] arr = {1, 2, 3, 4, 5},还有一个 斐波那契数组 int[] f = {1, 1, 2, 3, 5, 8, 13},此时需要新创建一个数组 temp,斐波那契数列中数当作成数组 temp的长度(length),比如,取斐波那契数组中的 f[5] = 8,作为数组 temp 的长度,将数组 arr (长度为 8)中的值拷贝到数组 temp 中, 那么,temp = {1, 2, 3, 4, 5, 0, 0, 0},再将数组 arr 中的最后一位数值都填冲到 数组 temp 中的 0 位置,也就是将 0 替换成 5。基本思想: 在斐波那契数列中,找一个等于或大于数组 arr 长度的数值 F[k],再将原数组 arr 进行扩充,也就是新创建一个数组 temp,扩充的大小为 F[k],(在这里,再强调一下,斐波那契数组中的值,就是新数组 temp 的长度),多余的部分,拿 arr 中最后一位数填充,再通过 F[k -1] -1 前部分,F[k - 2] - 1 后部分递归查找目标值。
三、代码实现
package com.xoste.algorithm.search;
import java.util.Arrays;
/**
* 斐波那契查找
* @author xoste
* @date 2022/4/17 12:54
*/
public class FibonacciSearch {
private static final int CAP = 20;
public static int[] fib() {
int[] f = new int[CAP];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < CAP; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
/**
* @param arr 数组
* @param target 目标值
* @return 返回对应的下标,如果没有返回 -1
*/
public static int fibSearch(int[] arr, int target) {
int low = 0;
int high = arr.length - 1;
// 表示斐波那契数组的下标索引
int k = 0;
// 存放 mid 值
int mid = 0;
// 获取斐波那契数列
int[] fib = fib();
// 获取斐波那契分割数值的下标(当 arr.length >= fib[k] - 1 时,才能获取斐波那契数值下标
while (arr.length >= fib[k] - 1) {
k++;
}
// 因为 fib[k] 的值可能大于 arr 的长度,因此需要构造一个新的数组,并指向 arr[]
int[] temp = Arrays.copyOf(arr, fib[k]);
// 如果 fib[k] > arr.length,将新的数组 temp 中大于 arr.length 的索引位置填充 arr[] 中最后一位的数值
// temp = {1, 8, 10, 89, 1000, 1234, 0, 0, 0} => {1, 8, 10, 89, 1000, 1234, 1234, 1234, 1234};
for (int i = high + 1; i < temp.length; i++) {
temp[i] = arr[high];
}
// 找出 target 目标值
while (low <= high) {
mid = low + fib[k - 1] - 1;
if (target < temp[mid]) {
// 向左扫描
high = mid - 1;
// 为什么 k - 1? 建议最好自己 Debug
k--;
} else if (target > temp[mid]) {
// 向右扫描
low = mid + 1;
// 为什么 k - 2? 建议最好自己 Debug
k -= 2;
} else {
if (mid <= high) {
return mid;
} else {
return high;
}
}
}
return -1;
}
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5};
int result = fibSearch(arr, 5);
System.out.println(result);
}
}